חזקה טבעית של פונקציה - חלק ג' - \(f^n{(x)}\)
\(f(x)\)
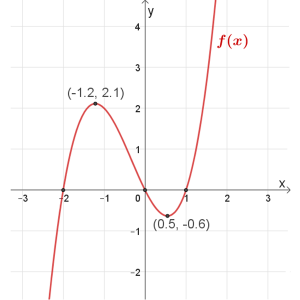
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-2,0)\)
נקודות קיצון: מקסימום \((-1.2,2.1)\) , מינימום \((0.5,-0.6)\)
- סרטטו באותה מערכת צירים, בצבעים שונים, את הגרפים של:
א. \(f^3(x)\)
ב. \(f^2(x)\) - באיזה תחום \(f^3(x)\le{f^2(x)}\)? (דייקו בתשובתכם ככל האפשר).
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף. - לאיזו פונקציה מבין הפונקציות \(f^3(x)\) , \(f^2(x)\), \(f(x)\) יש נקודות פיתול בהן שיפוע המשיק הוא אפס?
מה הם שיעורי נקודות אלה?
- במידת הצורך פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) ולפחות שבע נקודות צהובות (לסרטוט \(f^3(x)\)), במקומות המתאימים להן.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- כדי "לנקות" את היישומון ולהתחיל מחדש עם הפונקציה המוצגת, ניתן ללחוץ על אתחול.