שני משולשים במרובע ומעגל
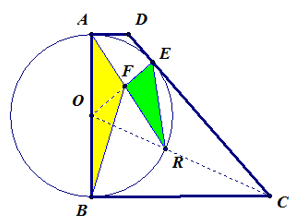
הוכיחו: שטח משולש \(\triangle AFB\) גדול פי 2 משטח משולש \(\triangle EFR\).
היעזרו ביישומון.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- גרירת נקודות \(A\) או \(E\), מציגה מרובע ומשולשים שונים, תוך שמירה על הנתונים.
- כדי ל"נקות" את היישומון ולהתחיל מחדש ניתן להיעזר בחיצי האתחול
 שבפינה הימנית העליונה.
שבפינה הימנית העליונה.





















