משפט תלמי
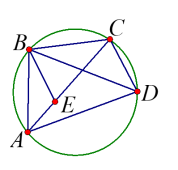
בניית עזר: העבירו קטע \(BE\) כך ש: \(\measuredangle CBD=\measuredangle ABE\)
- משולש \(ABC\) חסום במעגל.
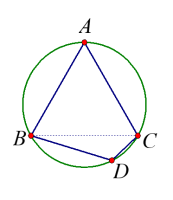
ונתון כי: \(AB=AC=BC\)
הנקודה \(D\) נמצאת על הקשת הקטנה \(BC\).
בטאו את שטח המרובע \(ABDC\) בעזרת \(AD\).
- במידת הצורך פתרו את הבעיות במדרגה 1.





















