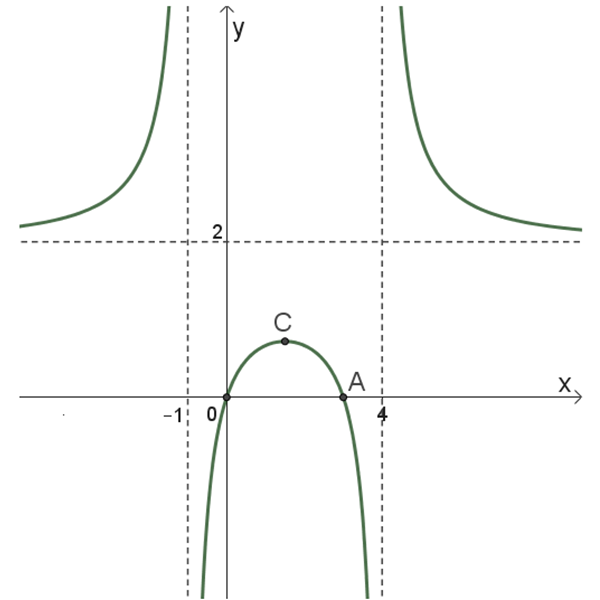
סעיף א

נתון כי: \(h'(x)=f^2(x)\cdot{f'(x)}\)

1. חשבו את האינטגרל הבא: \(\int\limits_{1.5}^{a}h'(x)dx\).
2. חשבו את האינטגרל הבא: \(\int\limits_{3.5}^{a+2}3\cdot{h'(x-2)}dx\) , נמקו תשובתכם.
3. נתון כי הנקודה \((0 ,0)\) נמצאת על גרף הפונקציה \(h(x)\), סרטטו סקיצה של גרף הפונקציה \(h(x)\).

סעיף ב

נסמן נקודה נוספת על גרף הפונקציה \(f(x)\): \(E(e,p)\) כך ש: \(1.5<e<a\).

נתון כי: \(t'(x)=\Large\frac{f'(x)}{f^2{(x)}}\)

1. בטאו, באמצעות הנתונים, את האינטגרל הבא: \(\int\limits_{1.5}^{e}t'(x)dx\) .
   האם ערך האינטגרל שמצאתם חיובי, שלילי או אפס? נמקו תשובתכם.
2. נתון כי הנקודה \((1.5 ,-1.389)\) נמצאת על גרף הפונקציה \(t(x)\).
   סרטטו סקיצה של גרף הפונקציה \(t(x)\).