מציאת יחס חלוקה – יחידות ההצגה של ווקטורים
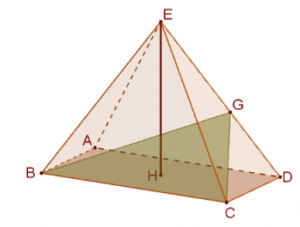
המישור שנקבע על-ידי הנקודות \(B\) , \(C\) , \(G\), חותך את גובה הפירמידה \(EH\).
\(H\) עקב הגובה במישור \(ABCD\).
נתון כי: \(\overrightarrow{AB}=\underline{u}\) , \(\overrightarrow{BC}=\underline{v}\) , \(\overrightarrow{EH}=\underline{w}\).
סמנו את נקודת החיתוך של המישור \(BCG\) עם הגובה \(EH\) ב-\(x\).
מטרתכם: למצוא את יחס החלוקה בין חלקי הגובה בהתאם לערכו של \(m\).
- בחרו קטע אותו תרצו לבטא בשתי דרכים שונות.
\(\space\) - הגדירו פרמטרים, ובטאו באמצעותם בשתי דרכים שונות את הקטע שבחרתם.
תנו דעתכם: מהו הביטוי האלגברי לעובדה שהנקודה x נמצאת במישור \(BCG\)?
\(\space\) - השתמשו בהצגות השונות ומצאו את יחס החלוקה בין חלקי הגובה בהתאם לערכו של \(m\).
\(\space\) - תארו את מקומה של הנקודה x במישור.
אם התקשיתם, תוכלו להציב, למשל, \(m=\Large\frac{1}{2}\) , ולפתור את הבעיה במקרה פרטי זה.





















