מנת חזקות של בינומים – כיצד זה נראה?
בעיית מטרה
לפניכם גרפים של פונקציות ורשימה של פונקציות מהמשפחה: \(f{(x)}=\Large\frac{(x-a)^n}{(x-b)^m}\) , \(a \ne b\) , m , n טבעיים גדולים מ- 1.
חלק א:
בכל שורה שני גרפים ושלוש פונקציות.
התאימו בין הגרפים לפונקציות והציעו סקיצה לפונקציה שאין לה גרף בשורה.
נמקו את תשובותיכם.
חלק ב:
אפיינו את הפונקציות במשפחה בהתאם לערכים של הפרמטרים.
תנו דעתכם על היחס בין a ל-b (מי גדול ממי, או שווה), הזוגיות של m ,n, והיחס ביניהם, והשפעה של אלה על תכונות הפונקציות.
א
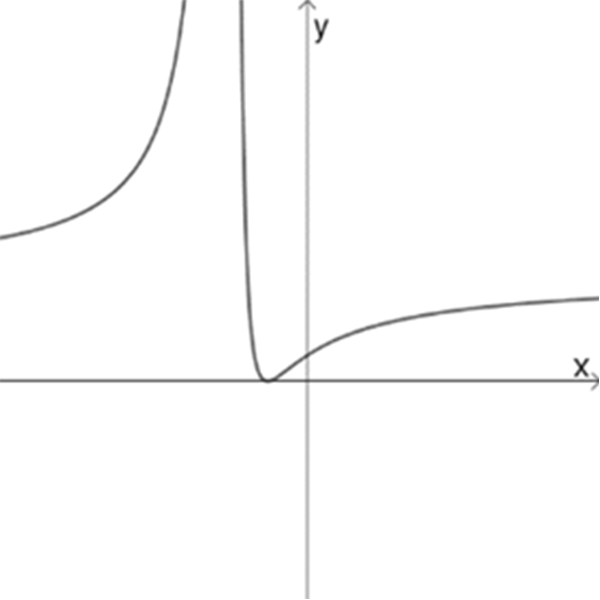
ב
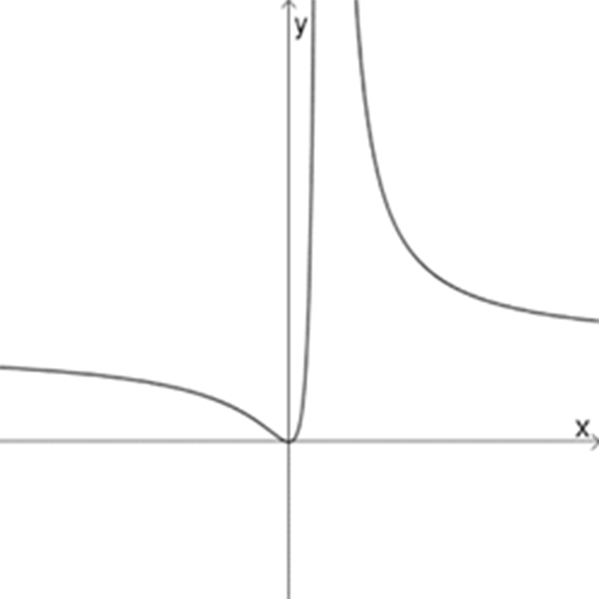
\(f_{1}(x)=\Large\frac{(x-2)^3}{(x-3)^2}\)
\(f_{2}(x)=\Large\frac{x^4}{(x-1)^4}\)
\(f_{3}(x)=\Large\frac{(x+1)^2}{(x+3)^2}\)
ג
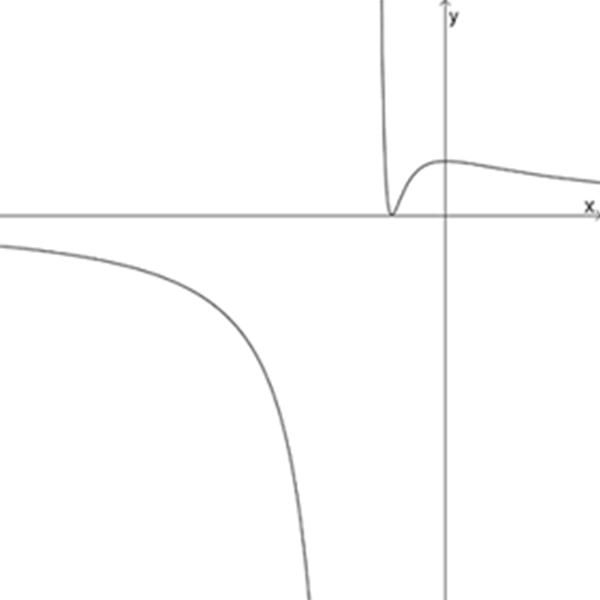
ד

\(f_{4}(x)=\Large\frac{(x+1)^2}{(x+2)^2}\)
\(f_{5}(x)=\Large\frac{(x+3)^2}{(x+2)^4}\)
\(f_{6}(x)=\Large\frac{(x+1)^2}{(x+2)^3}\)
ה
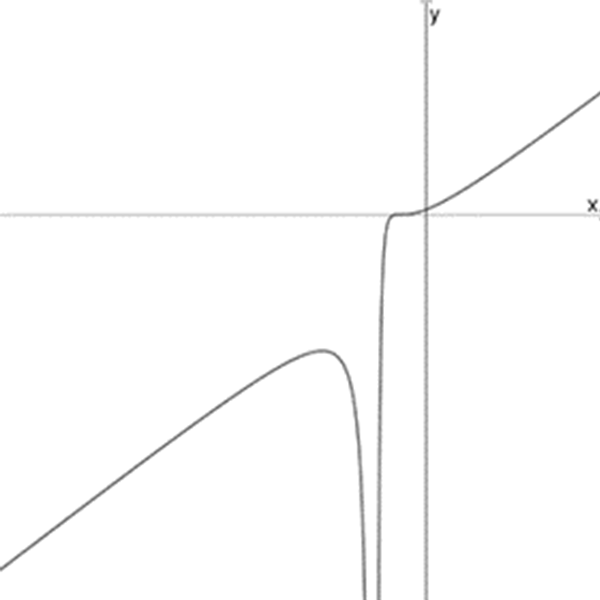
ו
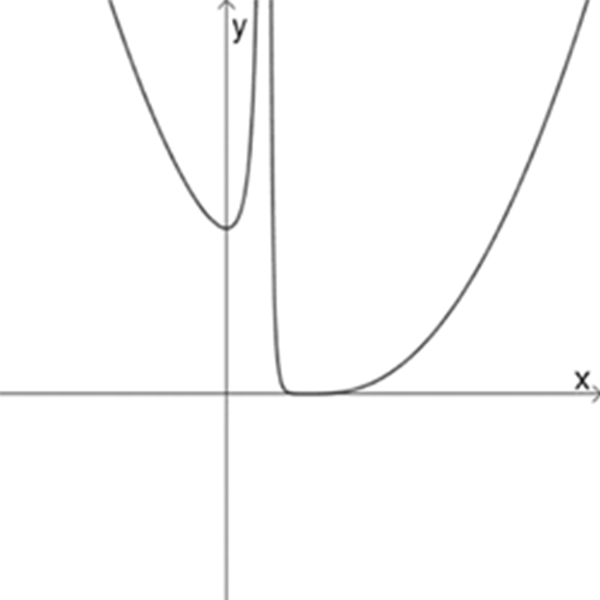
\(f_{7}(x)=\Large\frac{(x+1)^3}{(x+2)^2}\)
\(f_{8}(x)=\Large\frac{x^2}{(x-1)^2}\)
\(f_{9}(x)=\Large\frac{(x-2)^4}{(x-1)^2}\)
ז
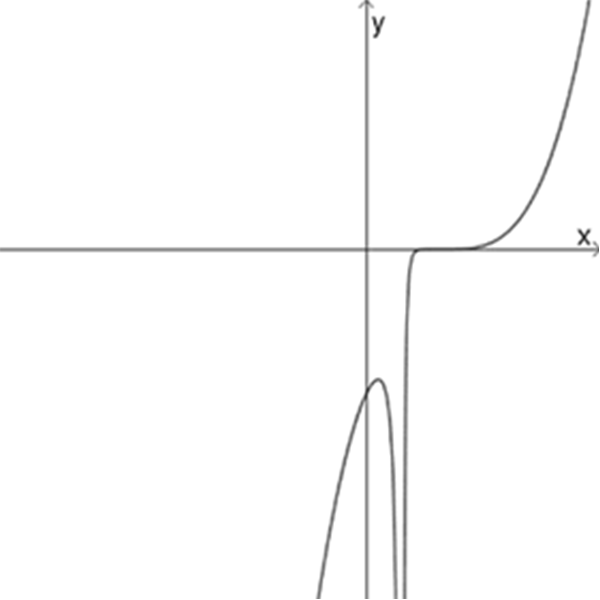
ח
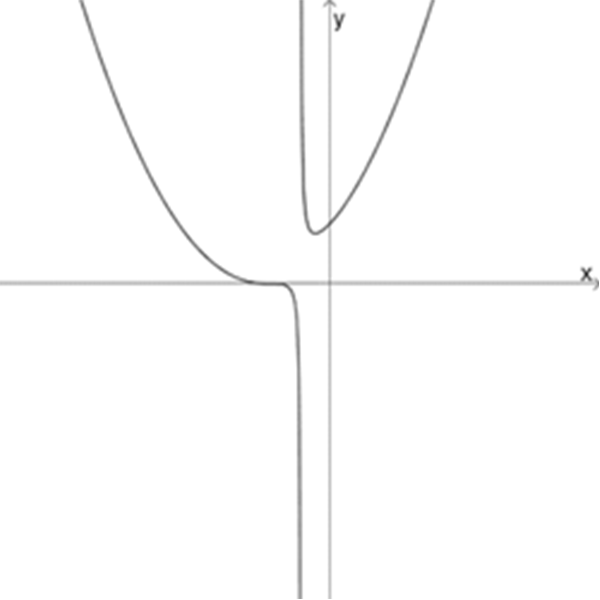
\(f_{10}(x)=\Large\frac{(x+2)^3}{x+1}\)
\(f_{11}(x)=\Large\frac{(x-3)^5}{(x-1)^2}\)
\(f_{12}(x)=\Large\frac{(x+2)^3}{(x+1)^2}\)
- במידת הצורך פתרו את הבעיות במדרגה 1.





















