פונקציה לוגריתמית מורכבת \(ln(f{(x)})\) - חלק ב'

בעיית אתגר

בסרטוט נתון גרף הפונקציה \(f(x)\).

  1. סרטטו באותה מערכת צירים בצבעים שונים את:
    \(ln(f{(x)})\) , \(ln(f^2{(x)})\) , \(ln(f^3{(x)})\) , \(ln(f^4{(x)})\).
    נמקו תשובותיכם.
    תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף.
  2. האם נכון לטעון כי עבור \(f(x)\) הנתונה מתקיים ש: \(ln(f^n{(x)})=n\cdot {ln(f(x))}\) לכל \(n\) טבעי?
    נמקו תשובתכם.

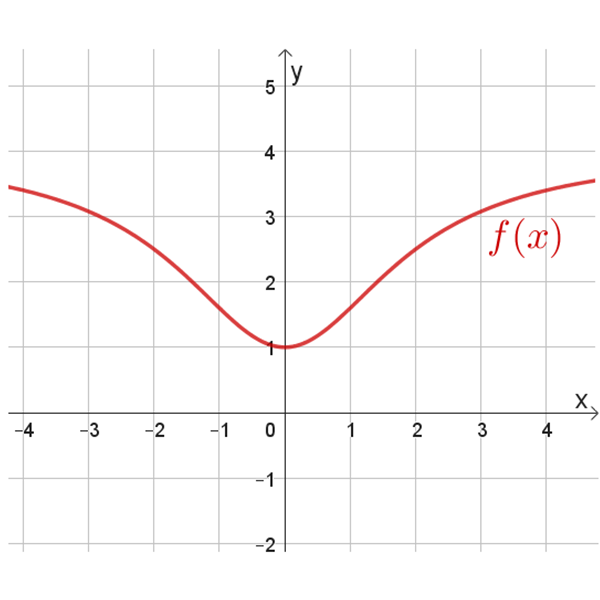
תחום הגדרה: כל \(x\)

נקודות החיתוך עם הצירים: \((0,1)\)

נקודת מינימום: \((0,1)\)

אסימפטוטה אופקית: \(y=4\)

  1. נתון כי: \(h(x)=f(x)-k\)

בכל אחד מהסרטוטים למטה נתונים הגרפים של: \(ln(h{(x)})\) , \(ln(h^2{(x)})\) , \(ln(h^3{(x)})\) , \(ln(h^4{(x)})\) עבור \(k\) מסוים.

מצאו מה יכולים להיות ערכי הפרמטר \(k\) בכל אחד מהסרטוטים.

נמקו תשובותיכם.

תוכלו לבדוק תשובתכם בעזרת היישומון המצורף.

א

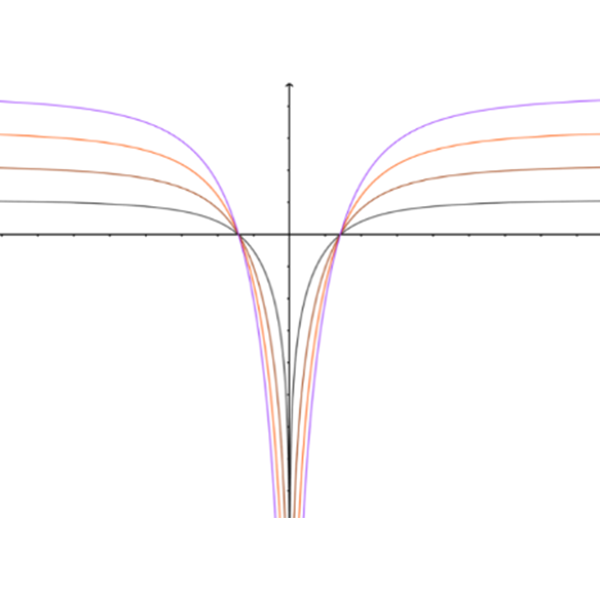
ב

יישומון

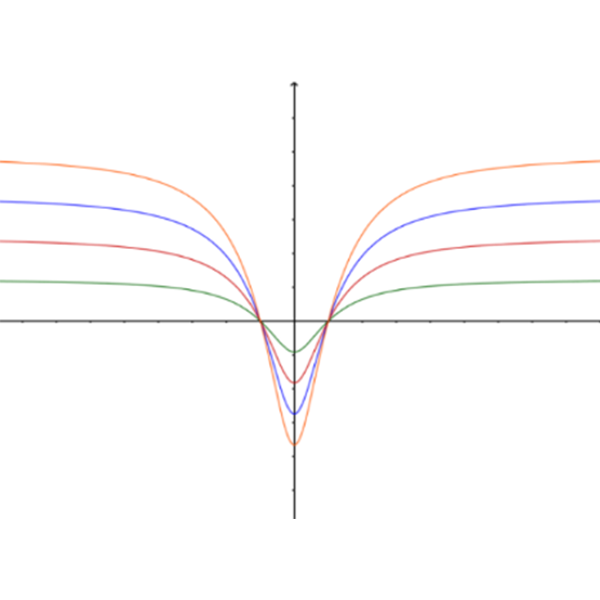
סעיף א

  • לשינוי המעריך (החזקה) של הפונקציה הלוגריתמית, ניתן לשנות את הערך של \(n\) בסרגל הגרירה.
  • בלחיצת מקש ימני בעכבר, כשהעכבר ממוקם על הגרף של \(ln(f{(x)})\) שמופיע ביישומון, יפתח תפריט:
  • לחיצה בתפריט על Trace on ואח"כ שינוי הערכים של \(n\) יגרמו לכך שניתן יהיה לראות את אוסף הפונקציות המתקבלות: \(ln(f{(x)})\) , \(ln(f^2{(x)})\) , \(ln(f^3{(x)})\) , \(ln(f^4{(x)})\).

סעיף ב

  • לצורך ניקוי המסך יש להיעזר בחיצי האתחול או בחץ undo שבפינה הימנית העליונה שבתפריט.
  • יש לקבוע תחילה את \(k\) בסרגל הגרירה, ואח"כ לשנות את \(n\) בסרגל הגרירה ולבדוק אם התמונה המתקבלת היא זו המבוקשת.