אינטגרלים ושטחים בשילוב הזזות והרכבה על פונקציה ליניארית - למורה
המשימה פותחה בהשראת משימה מאתר undergroundmathematics.
חומר לימוד:
הקשר בין שטחים לאינטגרלים בדגש על הרכבה של פונקציה על פונקציה ליניארית.
המשימה מתאימה לתרגול והעמקת ההבנה בהשפעה של הזזות והרכבה של פונקציה ליניארית על ערך האינטגרל.
כיתה:
כיתה י"א / כיתה י"ב
מבנה המשימה:
בעיית מטרה ושלוש מדרגות.
ידע קודם:
- הקשר בין אינטגרל לחישוב שטחים, חוקי אינטגרציה
מטרות לימודיות:
העמקת ההבנה בצורך שחלוקה בנגזרת הפנימית כאשר ההרכבה היא על פונקציה ליניארית.
משימת המטרה:
בבעייה סרטוט מורכב, שבו, מתוך נתונים ויזואליים ואנליטיים, צריך לחשב אינטגרל. בבעיה מופיעים 3 גרפים. בחישובי השטחים יש התייחסות לשיקופים, הזזות, מתיחות וכיווצים.
מדרגה 1:
בעיה דומה לבעיית המטרה: שלושה גרפים, המתקבלים זה מזה בהזזות, שיקופים ומתיחות. ברמת מורכבות מעט פשוטה יותר.
מדרגה 2:
שתי בעיות, באחת יש התייחסות להשפעה של הזזה אנכית בשילוב שיקוף ביחס לציר \(x\) ומתיחה אנכית, בשניה יש התייחסות להשפעה של הזזה אנכית בשילוב שיקוף ביחס לציר \(x\) ומתיחות אופקית ואנכית.
מדרגה 3:
שתי בעיות, באחת יש התייחסות להשפעה של הזזה אופקית ואנכית על שטחים ובשניה השפעה של שיקוף ביחס לציר \(y\) ומתיחה ביחס לציר \(y\).
אם עונים על כל הבעיות הפשוטות, המופיעות במדרגות 2 ו-3 נוגעים בכל הסוגיות שמובילות לפתרון בעיית המטרה.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות. המורה יציג את בעיית המטרה. התלמיד יכול לבחור לפי איזו רמה ברצונו לעבוד.
שימוש ביישומונים:
אין
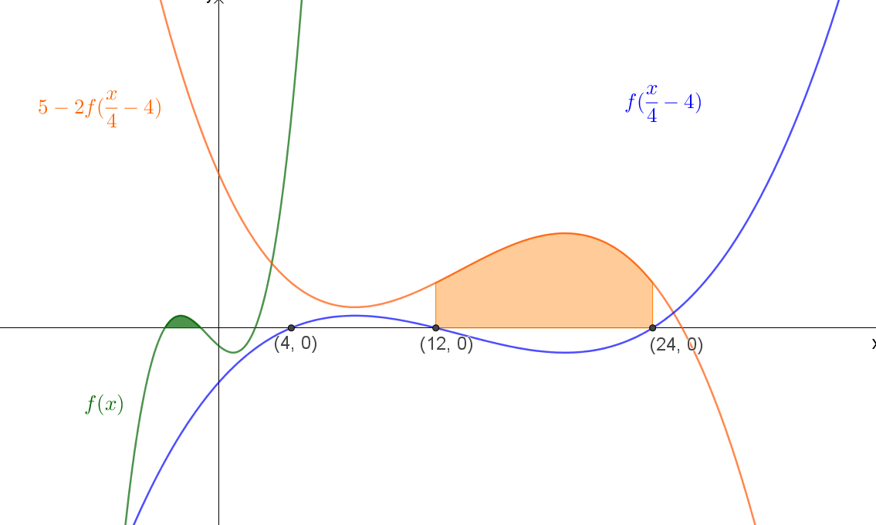
חשבו:
\(\int\limits_{4}^{24}{f(\Large\frac{x}{4}\normalsize-4)}dx=?\)
- במידת הצורך פתרו את הבעיות במדרגה 1.
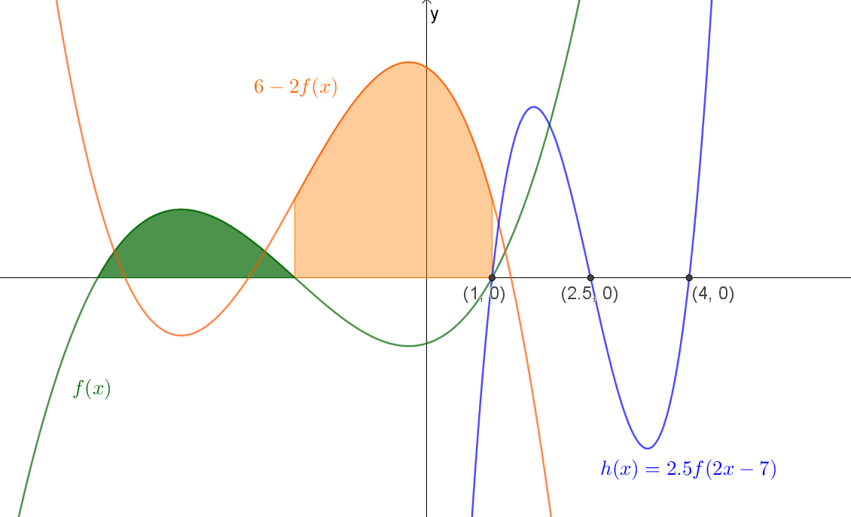
חשבו את:
\(\int\limits_{1}^{4}{h(x)}dx\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
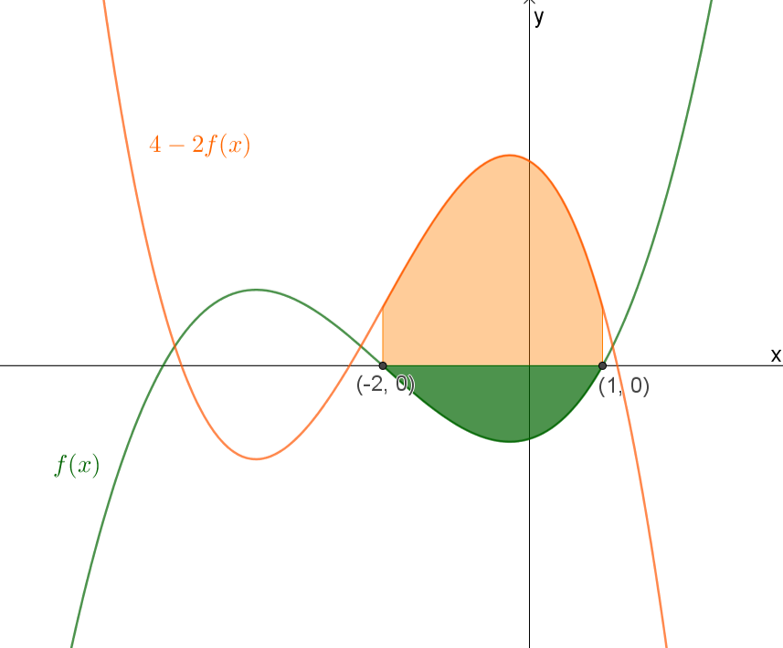
- הביטו בסרטוט הבא, זהו את הנתונים וחשבו את הנדרש:
נתון:
\(\int\limits_{-2}^{1}{f(x)}dx=-2\)
חשבו את גודל השטח הכתום.
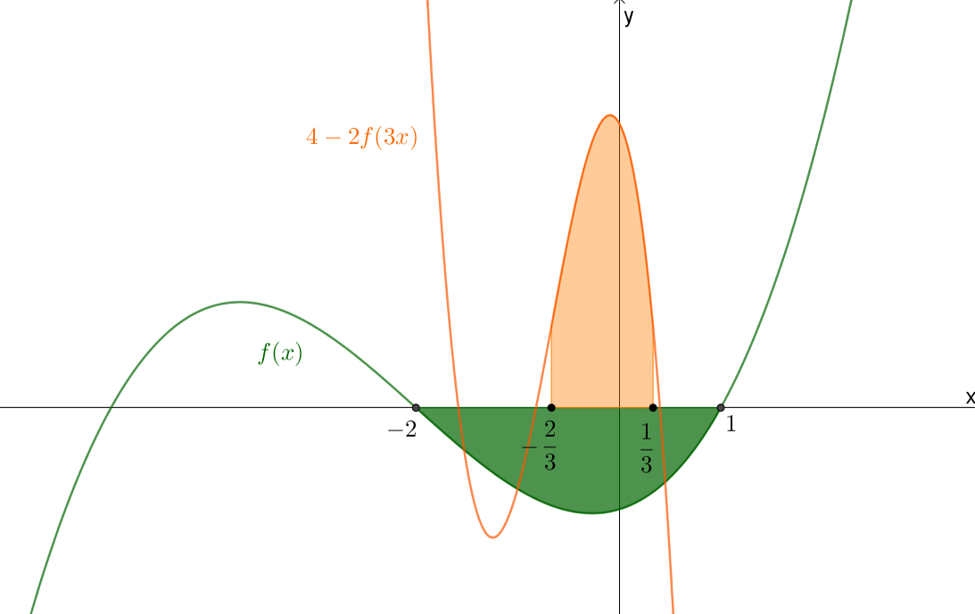
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
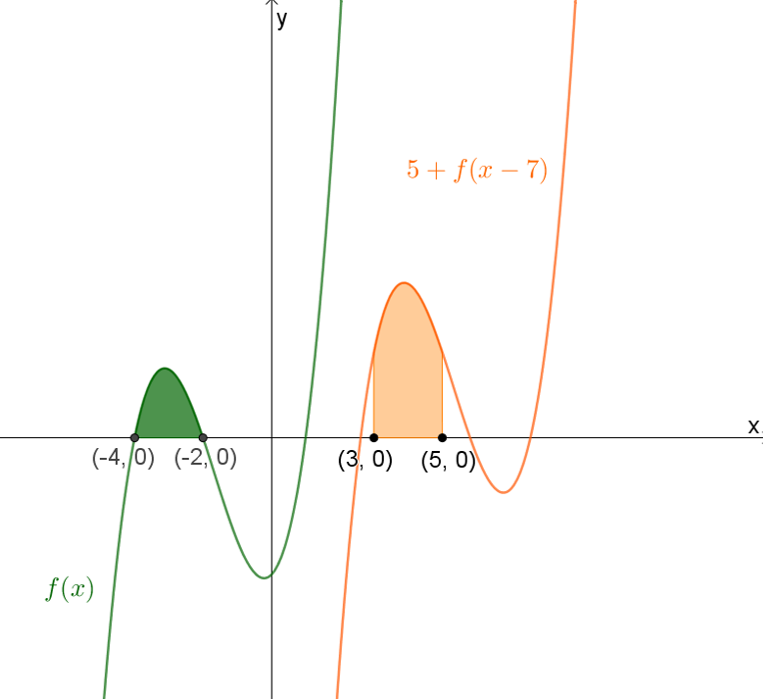
- הביטו בסרטוט הבא, זהו את הנתונים וחשבו את הנדרש:
נתון:
\(\int\limits_{-4}^{-2}{f(x)}dx=2\)
חשבו את גודל השטח הכתום.
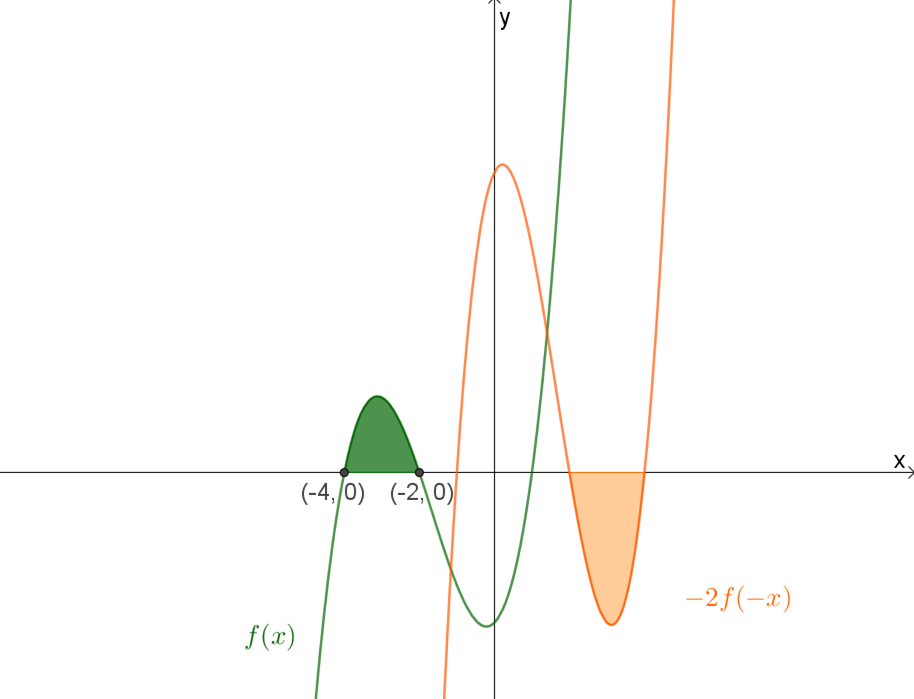
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















