אסימפטוטות או "חורים" בפונקציות מנה - חלק א' - למורה
חומר לימוד:
חקירה של משפחות של פונקציות רציונאליות שמאפשרות נקודות אי-רציפות סליקה ("חור").
החקירות במשימה מזמנות פיתוח מיומנות של הבחנה בין נקודות אי-רציפות בהן יש אסימפטוטה אנכית לבין נקודות בהן יש "חורים", לפי בחינת הקשר בין איפוס מכנה לאיפוס מונה.
כיתה:
כיתה י"א
מבנה המשימה:
בעיית מטרה ושתי מדרגות. לבעיית המטרה יש יישומון בו ניתן להיעזר לצורך החקירה.
ידע קודם:
- מיומנויות חקירה של פונקציה
- זיהוי אפסים של מונה ומכנה
- חקירת ביטוי ריבועי לפי פרמטר
- זיהוי אסימפטוטות אנכיות ואופקיות, זיהוי "חורים" – נקודות אי-רציפות סליקות
מטרות לימודיות:
- הבחנה בין אסימפטוטה אנכית לבין נקודת אי-רציפות סליקה – "חור".
- חקירה עם פרמטר בדגש על מספר אפסים של ביטוי ריבועי והשפעתו על פונקציה רציונאלית (איפוס מונה, איפוס מכנה).
הערה:
לנושא זה עוד שתי משימות, אסימפטוטות או "חורים" בפונקציית מנה, חלק ב' וחלק ג'.
משימת המטרה:
נתונה פונקציה רציונאלית, המונה והמכנה ממעלה שניה. במונה פרמטר אחד. יש למצוא ערכים של הפרמטר עבורם יש לפונקציה שתי אסימפטוטות אנכיות, אסימפטוטה אנכית אחת, אסימפטוטה אנכית ונקודת אי רציפות, אין אסימפטוטות אנכיות.
מדרגה 1:
נתונות ארבע פונקציות רציונליות, המונה והמכנה ממעלה שניה, וארבעה גרפים. יש להתאים בין הפונקציה לגרף המתאר אותה.
מדרגה 2:
נתונות שלוש פונקציות מנה, המונה והמכנה ממעלה שניה. יש לקבוע למי מהן שתי אסימפטוטות אנכיות ולמי אסימפטוטה אחת ונקודת אי הגדרה נוספת.
שיטת הוראה:
בכיתה:
עבודה בזוגות או בקבוצות. הכוונה למדרגות השונות ע"י המורה או לפי רצונו של התלמיד.
שימוש ביישומונים:
קיים יישומון לבעיית המטרה.
שיעורי בית:
ניתן לתת את חלקים ב' וג' כשיעורי בית. או להתחיל באחד מהחלקים האחרים ולתת את חלק א' כשיעורי בית.
משימות מומלצות:
בעיית מטרה
נתונה משפחת הפונקציות: \(g(x)=\Large\frac{x^2-2x+c}{x^2-4x}\) , \(c\) פרמטר.
מצאו במשפחה הנתונה, במידת האפשר, בהתאם לערכים שונים של הפרמטר, פונקציות:
- בעלות שתי אסימפטוטות מאונכות לציר x וללא נקודות חיתוך עם ציר ה-x.
- בעלות שתי אסימפטוטות מאונכות לציר x ושתי נקודות חיתוך עם ציר ה-x.
- בעלות שתי אסמפטוטות מאונכות לציר x ונקודת חיתוך אחת עם ציר ה-x.
- בעלות אסימפטוטה אנכית אחת בלבד וללא נקודת אי-הגדרה נוספת.
- בעלות אסימפטוטה אנכית אחת בלבד ונקודת אי הגדרה נוספת.
- ללא אסימפטוטה אנכית כלל.
בחקירתכם: תוכלו לבדוק תשובותיכם באמצעות היישומון המצורף. - השלימו חקירה עד לקבלת סקיצה לגרף עבור: \(g(x)=\Large\frac{x^2-2x+c}{x^2-4x}\)
במקרים הבאים: \(c=-8\) , \(c=0\).
- במידת הצורך פתרו את הבעיות במדרגה 1.
\(f_{3}(x)=\Large\frac{x^2-4x-12}{x^2-2x}\)
\(f_{4}(x)=\Large\frac{x^2-4x+10}{x^2-2x}\)
\(f_{1}(x)=\Large\frac{x^2-4x+4}{x^2-2x}\)
\(f_{2}(x)=\Large\frac{x^2-4x}{x^2-2x}\)
א

ב
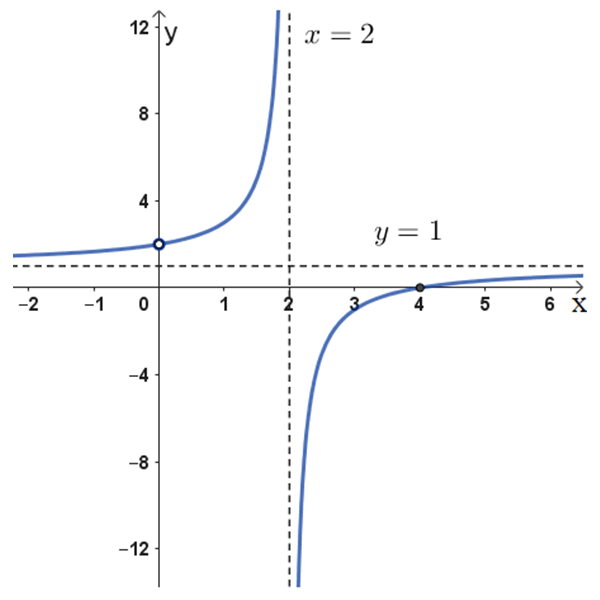
ג
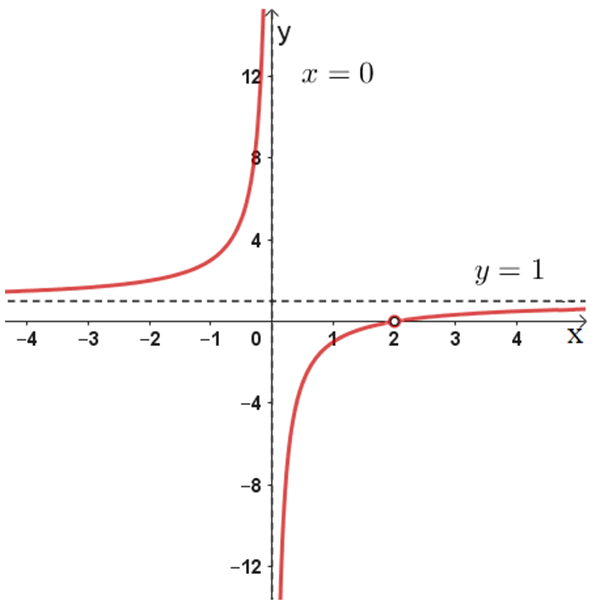
ד
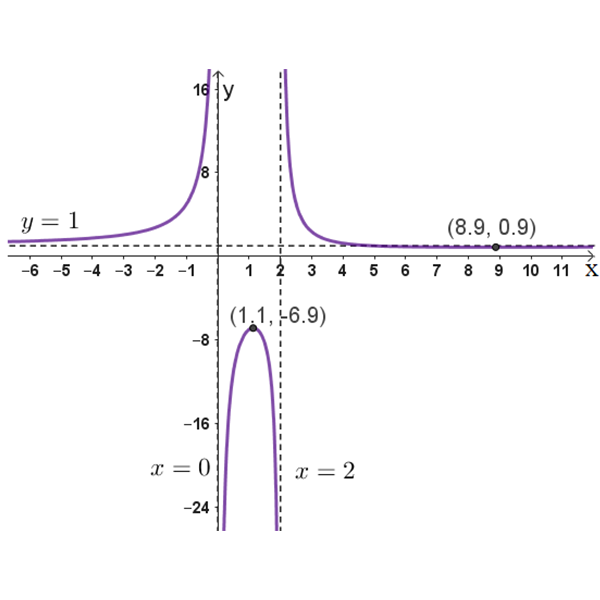
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
\(h(x)=\Large\frac{x^2-2x-8}{x^2-4x}\)
\(g(x)=\Large\frac{x^2-2x-3}{x^2-4x}\)
\(f(x)=\Large\frac{x^2-2x+1}{x^2-4x}\)
- לאילו מהפונקציות יש שתי אסימפטוטות אנכיות?
- איזו מהפונקציות בעלת אסימפטוטה אנכית אחת בלבד ונקודת אי הגדרה נוספת?
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.





















