הקשר בין גרף פונקציה לגרף הנגזרת שלה – המקרה של פולינום - למורה
חומר לימוד:
סרטוט איכותני של גרף נגזרת לגרף נתון של פונקציה, ללא ביטויים אלגבריים נתונים. במשימה נבנים הקשרים בין הגרף של פולינום לגרף של פונקציית הנגזרת הראשונה שלו. הדגש הוא על המימד הויזואלי/גרפי.
כיתה:
כיתה י'
מבנה המשימה:
בעיית מטרה ובהמשכה שלוש מדרגות. מצורפים יישומונים.
ידע קודם:
- הכרות עם פולינומים
- מיומנות חקירה בסיסית – שימוש בנגזרת ראשונה לקביעת תחומי עליה וירידה ונקודות קיצון
- הבנת המושג שיפוע משיק לגרף
מטרות לימודיות:
- הסקת תכונות של גרף הנגזרת הראשונה מגרף הפונקציה ולהיפך
- זיהוי גרף פונקציה וגרף נגזרת בין זוגות גרפים
סוג הדירוג:
משימת המטרה:
גרף של פונקציה בעלת 3 נקודות קיצון ושתי נקודות איפוס נגזרת שאינן נקודות קיצון.
מדרגה 1:
גרפים של שתי פונקציות מעט פשוטות יותר ביחס לאלו המופיעות במשימת המטרה.
מדרגה 2:
גרפים של 3 פונקציות בצירוף שאלות מנחות לחיפוש הקשרים בין גרף הפונקציה לגרף הנגזרת שלה.
מדרגה 3:
שני גרפים בצירוף טבלה לאיסוף ורישום נתונים לצורך איתור הקשרים בין גרף פונקציה לגרף של הנגזרת שלה.
במדרגה 1 הפונקציות מורכבות יותר מאשר במדרגה 2 ובמדרגה 2 מורכבות יותר מאשר במדרגה 3.
אם עונים על הבעיות במדרגות, נוגעים בכל הסוגיות המובילות לפתרון בעיית המטרה.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות, על בעיות מותאמות ליכולת. לצד כל משימה גם רמזים/שאלות מנחות לפתרונה.
כל התלמידים יתמודדו עם פונקציות ברמה הנדרשת לפי תכנית הלימודים.
תלמידים שלא מסיימים את העבודה בכיתה, יסיימו אותה בעבודה עצמאית בבית. בשיעור העוקב יש לקיים דיון מסכם לפעילות.
שימוש ביישומונים:
יש יישומונים לבעיית המטרה ולכל אחת מהמדרגות.
שיעורי בית:
תלמידים שלא מסיימים את העבודה בכיתה, יסיימו אותה בעבודה עצמאית בבית.
בשיעור העוקב יש לקיים דיון מסכם לפעילות.
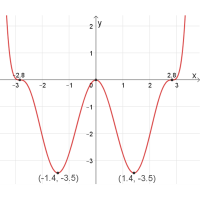
נקודות חיתוך של \(f(x)\) עם הצירים:
\((2.8 ,0)\) , \((0 ,0)\) , \((-2.8 ,0)\)
נקודות קיצון: מקסימום: \((0 ,0)\) מינימום: \((1.4 ,-3.5)\) , \((-1.4 ,-3.5)\)
נקודות פיתול: \((2.8 ,0)\) , \((-2.8 ,0)\)
מטרתכם: לסרטט סקיצה לגרף הנגזרת \(f'{(x)}\), עבור הפונקציה הנתונה באיור.
תנו דעתכם לתחומי החיוביות והשליליות של הנגזרת ולנקודות הקיצון שלה.
תוכלו להיעזר ביישומון.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- כאשר גוררים את הנקודה האדומה, המסומנת על הגרף, ניתן לראות כיצד נע איתה המשיק לגרף הפונקציה, וכך לחזות בשיפועיו המשתנים.
- מתוך מחסן הנקודות יש לגרור נקודות למקומות המתאימים להן לתאור הפונקציה המבוקשת.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה המבוקשת. - ניתן לבצע בדיקה לקבלת משוב.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
א
ב
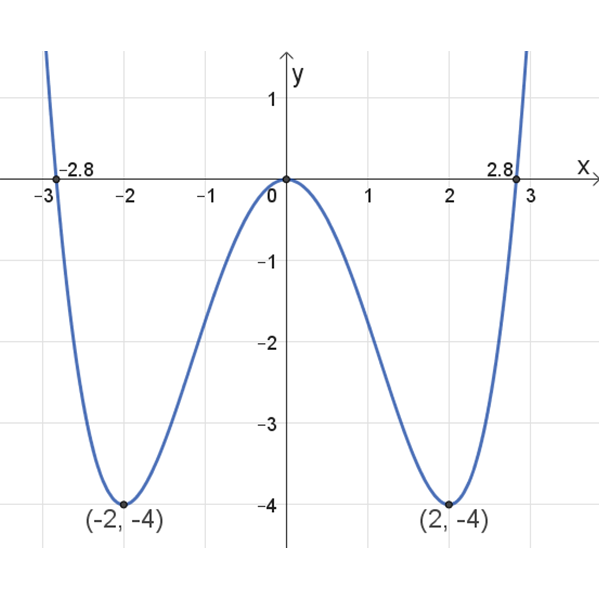
נקודות חיתוך עם הצירים:
\((2.8 ,0)\) , \((0 ,0)\) , \((-2.8 ,0)\)
נקודות קיצון: מקסימום: \((0 ,0)\) , מינימום: \((2 ,-4)\) , \((-2 ,-4)\)
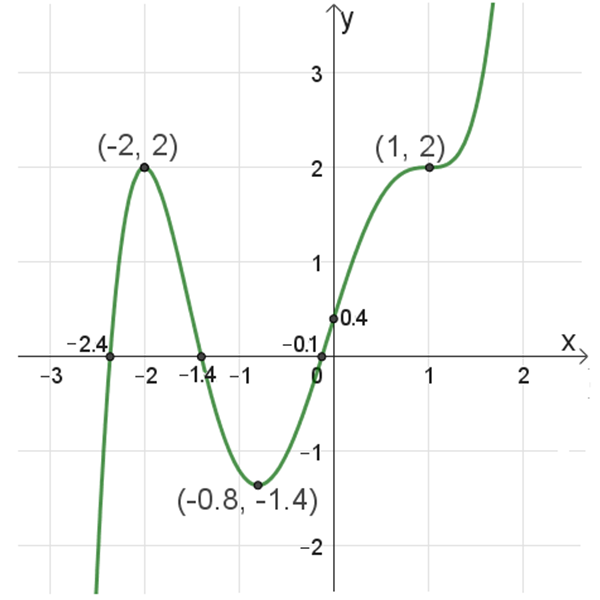
נקודות חיתוך עם הצירים:
\((0 ,0.4)\) , \((-0.1 ,0)\) , \((-1.4 ,0)\) , \((-2.4 ,0)\)
נקודות קיצון: מקסימום: \((-2 ,2)\) , מינימום: \((-0.8 ,-1.4)\)
נקודת פיתול: \((1 ,2)\)
תוכלו להיעזר ביישומון.
בסיום, הסיקו מסקנות:
- איפה (על גרף הפונקציה) לנגזרת יש נקודת קיצון?
- במה מתאפיין גרף הפונקציה בתחום עליה של הנגזרת?
- במה מתאפיין גרף הפונקציה בתחום ירידה של הנגזרת?
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- כאשר גוררים את הנקודה האדומה, המסומנת על הגרף, ניתן לראות כיצד נע איתה המשיק לגרף הפונקציה, וכך לחזות בשיפועיו המשתנים.
- מתוך מחסן הנקודות יש לגרור נקודות למקומות המתאימים להן לתאור הפונקציה המבוקשת.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה המבוקשת.
- ניתן לבצע בדיקה לקבלת משוב.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
פונקציה א
פונקציה ב
פונקציה ג
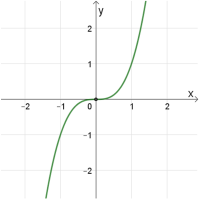
נקודת חיתוך עם הצירים: \((0 ,0)\)
נקודת פיתול: \((0 ,0)\)
נקודות חיתוך עם הצירים:
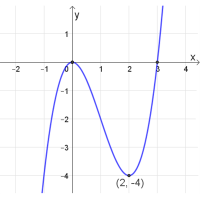
\((3 ,0)\) , \((0 ,0)\)
נקודות קיצון: מקסימום: \((0 ,0)\), מינימום: \((2 ,-4)\)
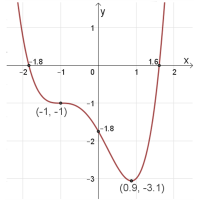
נקודות חיתוך עם הצירים:
\((1.6 ,0)\) , \((0 ,-1.8)\) , \((-1.8 ,0)\)
נקודת קיצון: מינימום: \((0.9 ,-3.1)\)
נקודת פיתול: \((-1 ,-1)\)
סרטטו סקיצה לגרף הנגזרת , עבור פונקציה א', עבור פונקציה ב' ועבור פונקציה ג'.
תנו דעתכם לתחומי החיוביות והשליליות של הנגזרת ולנקודות הקיצון שלה.
תוכלו להיעזר ביישומונים (לכל פונקציה יישומון משלה).
בכל יישומון, תוכלו להיעזר בכלי העפרון שבסרגל העליון, או בסימון נקודות מיוחדות בגרף הנגזרת.
גררו את הנקודה המסומנת על פני גרף הפונקציה ובחנו את שיפועי המשיקים.
עבור כל אחד מהגרפים, נסו לבנות גרף נגזרת, תוך התייחסות לתכונות של הגרף:
סעיף א
- שיפועי המשיקים,
- תחומי החיוביות והשליליות שלו,
- תחומי העלייה והירידה שלו (ככל שתוכלו לדייק).
סעיף ב
ענו על השאלות הבאות:
- מה מתרחש בגרף הנגזרת כאשר לפונקציה יש נקודת קיצון?
- כיצד אפשר להבחין בין נקודת מינימום לנקודת מקסימום של הפונקציה לפי גרף הנגזרת?
- מה קורה בפונקציה כאשר לנגזרת יש נקודת חיתוך עם ציר x?
- מה קורה בנגזרת כאשר לפונקציה יש נקודה שבה שיפוע המשיק אפס, אך היא אינה משנה מגמה, כלומר, ממשיכה לעלות או ממשיכה לרדת?
- איפה (על גרף הפונקציה) לנגזרת יש נקודת השקה לציר ה-x, שהיא נקודת מקסימום? מינימום?
- נסו להסביר גם איפה לנגזרת יש נקודת קיצון מסוג מינימום? מסוג מקסימום?
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- כאשר גוררים את הנקודה האדומה, המסומנת על הגרף, ניתן לראות כיצד נע איתה המשיק לגרף הפונקציה, וכך לחזות בשיפועיו המשתנים.
- מתוך מחסן הנקודות יש לגרור נקודות למקומות המתאימים להן לתאור הפונקציה המבוקשת.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה המבוקשת.
- ניתן לבצע בדיקה לקבלת משוב.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
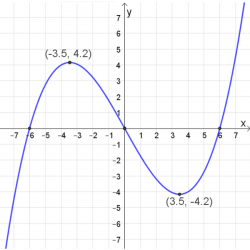
נקודות חיתוך עם הצירים:
\((6 ,0)\) , \((0 ,0)\) , \((-6 ,0)\)
נקודות קיצון: מקסימום: \((-3.5 ,4.2)\) מינימום: \((3.5 ,-4.2)\)
סעיף א
מטרתכם: לסרטט סקיצה לגרף הנגזרת.
תוכלו להיעזר ביישומון. גררו את הנקודה המסומנת על פני גרף הפונקציה ובחנו את שיפועי המשיקים.
נסו לבנות גרף נגזרת, תוך התייחסות לתכונות של הגרף:
- שיפועי המשיקים,
- תחומי החיוביות והשליליות שלו,
- תחומי העלייה והירידה שלו (ככל שתוכלו לדייק).
תוכלו להיעזר בטבלה הבאה לאיסוף נתונים:
הפונקציה \(f_{1}{(x)}\)
\(x\)
\(f{(x)}\)
שיפוע המשיק
הנקודה \((x , f'{(x)})\)
באמצעות אוסף הנקודות שרשמתם, בנו במחברתכם גרף שמתאר את "פונקציית שיפועי המשיקים" – גרף הנגזרת הראשונה.
סעיף ב
בדקו את עצמכם: סרטטו את גרף הנגזרת באמצעות היישומון ובדקו את ההתאמה לתשובתכם.
סעיף ג
תארו את גרף הנגזרת שקיבלתם מבחינת:
- תחומי החיוביות והשליליות שלו.
- תחומי העליה והירידה שלו (ככל שתוכלו לדייק).
סעיף ד
הסיקו מסקנות ככל שתוכלו:
- מה מתרחש בגרף הנגזרת כאשר לפונקציה יש נקודת קיצון?
- כיצד אפשר להבחין בין נקודת מינימום לנקודת מקסימום של הפונקציה לפי גרף הנגזרת?
- מה קורה בפונקציה כאשר לנגזרת יש נקודת חיתוך עם ציר x?
- כאשר גוררים את הנקודה האדומה, המסומנת על הגרף, ניתן לראות כיצד נע איתה המשיק לגרף הפונקציה, וכך לחזות בשיפועיו המשתנים.
- מתוך מחסן הנקודות יש לגרור נקודות למקומות המתאימים להן לתאור הפונקציה המבוקשת.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה המבוקשת.
- ניתן לבצע בדיקה לקבלת משוב.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
פונקציה 2
חזרו שוב על המשימה הקודמת עבור פונקציה \(f_{2}{(x)}\) המתוארת בגרף הבא:
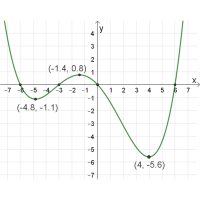
נקודות חיתוך עם הצירים:
\((6 ,0)\) , \((0 ,0)\) , \((-3 ,0)\) , \((-6 ,0)\)
נקודות קיצון: מקסימום:\((-1.4 ,0.8)\) מינימום: \((4 ,-5.6)\) , \((-4.8 ,-1.1)\)
שערו כיצד נראה גרף הנגזרת לפני השימוש ביישומון.
לאחר שתסרטטו את גרף הנגזרת, השתמשו ביישומון ובדקו השערתכם.
תוכלו, גם כאן, כמובן, להשתמש בטבלה שמופיעה בשאלה 1.
הקפידו לענות שוב על כל השאלות שמופיעות בשאלה 1.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.