סינוסים או קוסינוסים – איך לבחור פתרון – למורה

סינוסים או קוסינוסים – איך לבחור פתרון - למורה

יישומונים

יישומון – בעיית מטרה
- יישומון – מדרגה 1
- – – – – –
- – – – – –

חומר לימוד:

פתרון בעיות טריגונומטריות במישור באמצעות משפט הסינוסים או משפט הקוסינוסים בבעיות בהן נדרש שימוש במשפטים הנ"ל במשולשים שונים. התהליך מזמן מכשלות בדמות הצורך לבחור פתרון נכון בין שניים שונים.

במיוחד נבחן היתרון של השימוש במשפט הקוסינוסים במקרים בהם ידועים נתונים מסוג צ.צ.ז. ונבחן הצורך לבחור בין אפשרויות במקרה שידועים יותר משלושה נתונים במשולש. תרגול מתקדם.

כיתה:

כיתה י"א

מבנה המשימה:

בעיית מטרה ושלוש מדרגות, בצירוף יישומונים לבעיית המטרה ולמדרגה 1.

ידע קודם:

משפט הסינוסים
משפט הקוסינוסים
משוואות טריגונומטריות אלמנטריות
ידע גיאומטרי בנושא מרובעים ומעגל

מטרות לימודיות:

התמודדות עם שאלות שיובילו למסקנה הבאה: השימוש במשפט הסינוסים במצב נתונים: צ.צ.ז. מול הקטנה בין השתיים יכול להוביל למסקנות שגויות. כשאפשר – עדיף להשתמש במשפט הקוסינוסים. יותר מכך – במצב בו ידועים במשולש יותר משלושה נתונים, יש לבחור בקפידה את הפתרון המתאים, שכן לעיתים תשובה שמתקבלת לא מתאימה לנתון הרביעי, בו לא השתמשנו בעת ההפעלה של משפט הסינוסים, או הקוסינוסים.

משימת המטרה:

בעיה עם פרמטרים. שימוש במשפט הסינוסים ובמשפט הקוסינוסים.

מדרגה 1:

בעיה מספרית, שימוש במשפטים: הסינוסים והקוסינוסים (אפשר גם בלי משפט הסינוסים).

מדרגה 2:

בעיה המכוונת לשימוש במשפט הקוסינוסים ובזהות: $sin⁡(x)=sin⁡(180^\circ-x)$ .

מדרגה 3:

בעיות בהן נתונות שתי צלעות והזווית שמול הקטנה מבין שתיהן.

שיטת הוראה:

בכיתה:

כדאי להנחות תלמידים לעבוד בזוגות או קבוצות הטרוגניות.

שימוש ביישומונים:

יישומונים לבעיית המטרה ולמדרגה 1.

בעיית מטרה

במעוין

A B C D

$ABCD$ הנקודה

E

$E$ היא אמצע הצלע

B C

$BC$ .

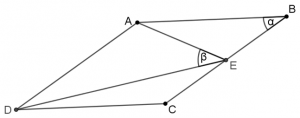
נתון כי: $\measuredangle ABC = \alpha$ , $\measuredangle AED = \beta$

הוכיחו כי: $cos \beta = \Large\frac{3}{\sqrt{25-16\cos^2 \alpha}}$
$\space$
נתון כי $\alpha=35^{\circ}$ . חשבו את $\measuredangle DAE$ .
$\space$
רז ועומר פתרו את סעיף ב והגיעו לתוצאות שונות.
רז מצאה: $\measuredangle DAE=119.09^{\circ}$
ועומר מצא: $\measuredangle DAE=60.91^{\circ}$
הכיצד??? ואיזה פתרון הוא הנכון? נמקו.

לפתרון סעיפים ב ו-ג תוכלו להיעזר ביישומון.

במידת הצורך פתרו את הבעיות במדרגה 1.

יישומון לסעיפים ב, ג

גרירת אחת הנקודות הכחולות ( $A$ או $B$ ) תשנה את גודל המעוין.
לחיצה על הנקודה האדומה, תציג פתרון נוסף, שיאפשר לקבוע איזה פתרון הוא הנכון.

מדרגה 1

הקודקודים $B$ ו- $C$ במשולש $ABC$ נמצאים על מעגל.

מרכז המעגל $O$ נמצא על הצלע $AB$ (ראו איור).

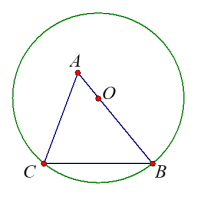
נתון: $AC=24 cm$ , $AO=8 cm$ , $\measuredangle BAC=60^{\circ}$

פתרו את הבעיות הבאות בשתי דרכים:

חשבו את רדיוס המעגל.
חשבו את אורך הצלע $BC$ .

תוכלו להיעזר ביישומון.

אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
או, במידת הצורך, פתרו את הבעיות במדרגה 2.

יישומון

בחירת הסעיף הנדרש מציגה רמזים לפתרון.
בחירת סעיף "המשך הפתרון" מציגה שתי אפשרויות לבחירה: שימוש במשפט הסינוסים או שימוש במשפט הקוסינוסים.

מדרגה 2

נתון מעוין $ABCD$ .

הנקודה $F$ נמצאת על הצלע $AB$ , כך ש $BF=2 AF$ .

נתון כי: $sin(\measuredangle DCB)=\Large\frac{\sqrt{3}}{2}$ .

מצאו את גודל הזווית $\measuredangle FCB$
כמה פתרונות לשאלה? (סרטטו סרטוט מתאים / סרטוטים מתאימים).

אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
או, במידת הצורך, פתרו את הבעיות במדרגה 3.

מדרגה 3

במשולש $ABC$ ידוע כי $BC$ היא הצלע הארוכה ביותר
וכן:
$BC = 13 cm$ , $AC = 9 cm$ , $\measuredangle ABC=35^{\circ}$ .
מהי מידת הזווית: $\measuredangle CAB$ ? כמה אפשרויות לפתרון?
הסבירו כיצד בחרתם את הפתרון הנכון / הפתרונות הנכונים.
$\space$
במשולש $ABC$ ידוע כי $BC$ היא הצלע הארוכה ביותר
וכן:
$BC=12 cm$ , $AC=11 cm$ , $\measuredangle ABC=60^{\circ}$ .
מהי מידת הזווית: $\measuredangle CAB$ ? כמה אפשרויות לפתרון?
הסבירו כיצד בחרתם את הפתרון הנכון / הפתרונות הנכונים.

מהו ההבדל בין הבעיות? איזו דרך מבטיחה פתרון מדויק ושלם?

אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.

משימות מדורגות
Stepped Tasks

משימות מדורגות
Stepped Tasks

משימות מדורגות

משימות מדורגות

משימות מדורגות

תוכנית מאור

מתמטיקה אוריינית בחטיבת הביניים

برنامج مأور – مهام تنور رياضي

משימות מדורגות
Stepped Tasks