סינוסים או קוסינוסים – איך לבחור פתרון
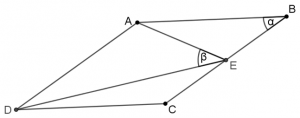
נתון כי: \(\measuredangle ABC = \alpha\) , \(\measuredangle AED = \beta\)
- הוכיחו כי: \(cos \beta = \Large\frac{3}{\sqrt{25-16\cos^2 \alpha}}\)
\(\space\) - נתון כי \(\alpha=35^{\circ}\). חשבו את \(\measuredangle DAE\).
\(\space\) - רז ועומר פתרו את סעיף ב והגיעו לתוצאות שונות.
רז מצאה: \(\measuredangle DAE=119.09^{\circ}\)
ועומר מצא: \(\measuredangle DAE=60.91^{\circ}\)
הכיצד??? ואיזה פתרון הוא הנכון? נמקו.
לפתרון סעיפים ב ו-ג תוכלו להיעזר ביישומון.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- גרירת אחת הנקודות הכחולות (\(A\) או \(B\)) תשנה את גודל המעוין.
- לחיצה על הנקודה האדומה, תציג פתרון נוסף, שיאפשר לקבוע איזה פתרון הוא הנכון.





















