פונקציות עם שורשים ריבועיים – מה ההבדל בינינו? חלק א'
א
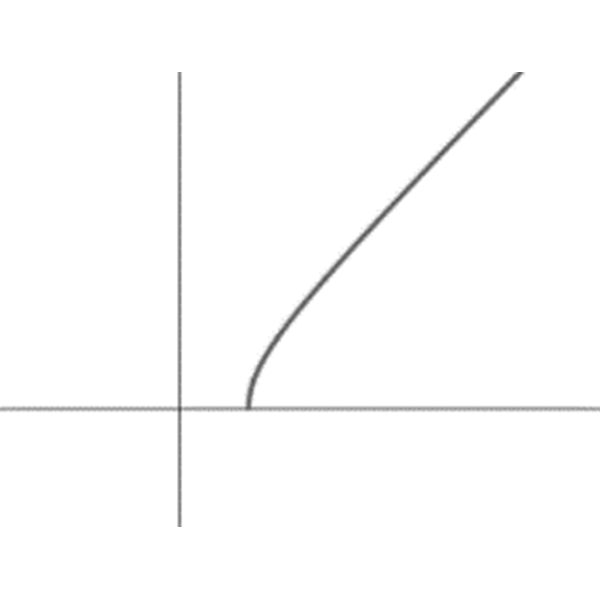
ב
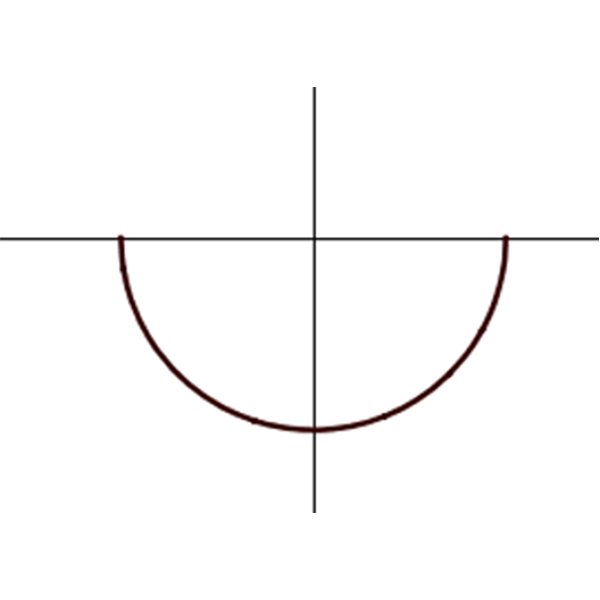
\(f_{1}(x)=-\sqrt{1-x^2}\)
\(f_{2}(x)=\sqrt{(x-1)}\cdot\sqrt{(x+1)}\)
\(f_{3}(x)=\sqrt{x^2-1}\)
ג
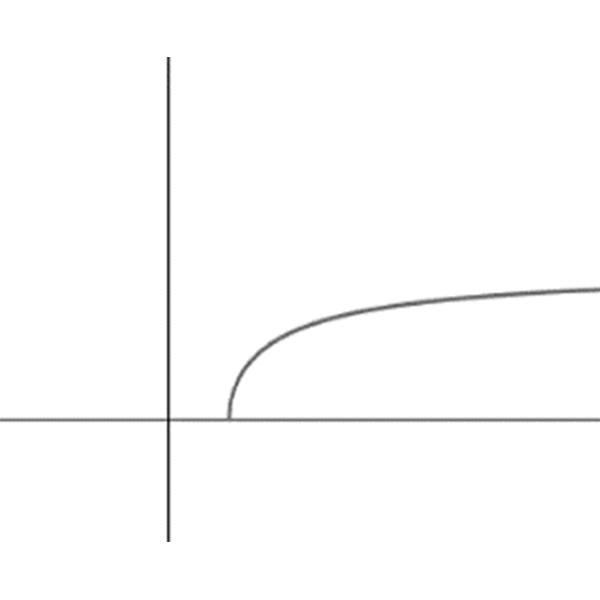
ד
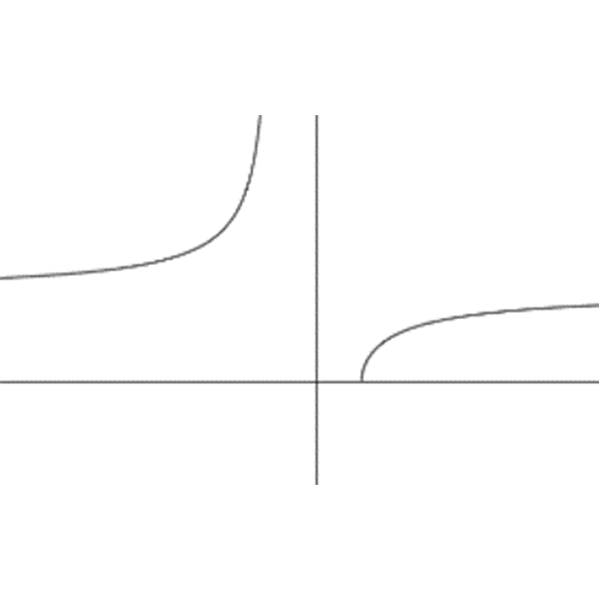
\(f_{4}(x)=\Large\frac{\sqrt{x-1}}{\sqrt{x+1}}\)
\(f_{5}(x)=\sqrt{\Large\frac{x-1}{x+1}}\)
\(f_{6}(x)=\Large\frac{\sqrt{1-x}}{\sqrt{x+1}}\)
ה
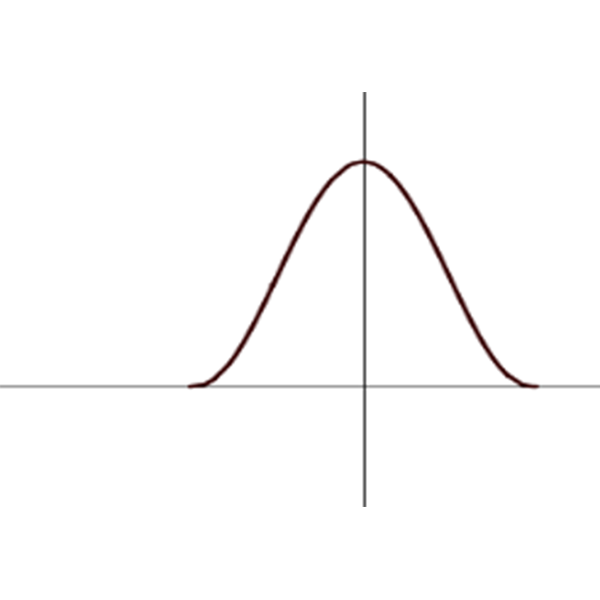
ו

\(f_{7}(x)=\sqrt{(1-x^2)^2}\)
\(f_{8}(x)=\sqrt{(1-x^2)^5}\)
\(f_{9}(x)=\sqrt{(1-x^2)^4}\)
- לכל אחד מהגרפים התאימו ביטוי מתוך שלושת הביטויים, אשר בשורה שלו, והוסיפו בעצמכם גרף עבור הביטוי הנותר בכל שורה.
- נסו להציע סקיצות ללא חקירה וללא שימוש במחולל גרפים.
- בידקו עצמכם באמצעות מחולל גרפים (כמו: geogebra או desmos). (לבעיה לא קיים יישומון).
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















