פונקציות עם שורשים ריבועיים – מה ההבדל בינינו? חלק ב'
א
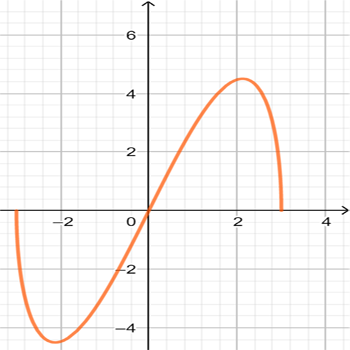
\(f_{2}(x)=\sqrt{x^2(9-x^2)}\)
\(f_{1}(x)=x\sqrt{9-x^2}\)
ב
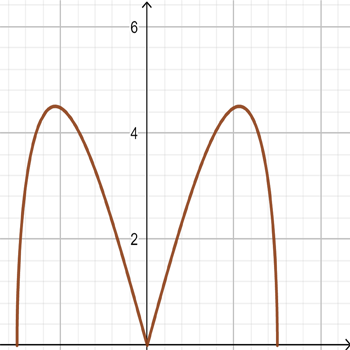
\(f_{4}(x)=\sqrt{x^2(9-x^2)}\)
\(f_{3}(x)=|x|\sqrt{9-x^2}\)
ג
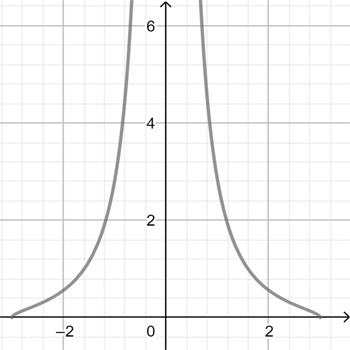
\(f_{6}(x)=\sqrt{\Large\frac{9-x^2}{x^4}}\)
\(f_{5}(x)=\Large\frac{\sqrt{9-x^2}}{x^2}\)
ד
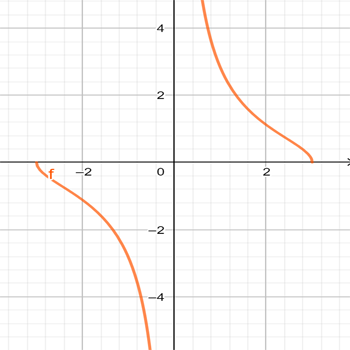
\(f_{8}(x)=\sqrt{\Large\frac{9-x^2}{x^2}}\)
\(f_{7}(x)=\Large\frac{\sqrt{9-x^2}}{x}\)
התאימו לכל גרף פונקציה. אם נחוץ, הוסיפו בעצמכם גרף לפונקציה השנייה.
נסו להציע סקיצות ללא חקירה וללא שימוש במחולל גרפים.
- בחנו את תחום ההגדרה של הפונקציות השונות.
- אפיינו את ההשפעה של השורש הריבועי על תחום ההגדרה ועל המראה של הגרף בקצוות התחום.
- השתמשו במחולל גרפים (כמו: geogebra או desmos) לצורך בדיקה. (לבעיה לא קיים יישומון).
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.





















