קשרים בין פונקציה \(f{(x)}\) לפונקציה ההופכית לה \(\frac {1}{f{(x)}}\) - חלק ג'
ביטויים עבור הפונקציה \(h_{n}{(x)}\)
\(h_{1}(x)=x^2(x-5)\)
\(h_{2}(x)=\Large\frac{(x+2)(3x-3)}{x-1}\)
\(h_{3}(x)=(x^2+1)(x^2+4)\)
\(h_{4}(x)=-x^3(x^2+1)\)
גרפים של הפונקציות \(h_{n}{(x)}\)
I
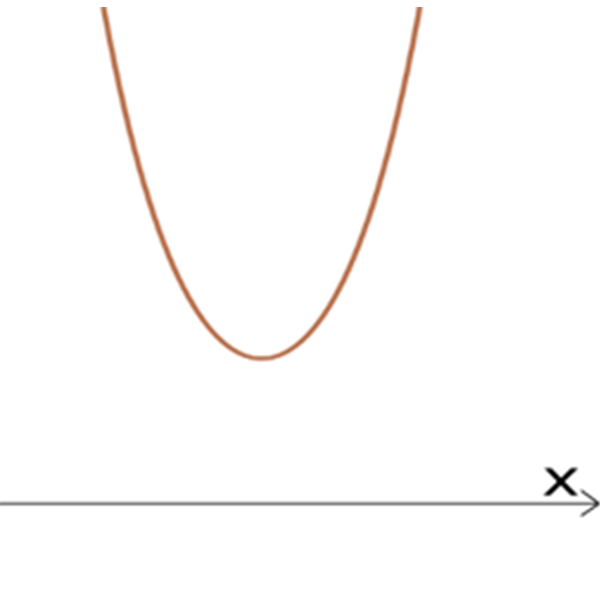
II
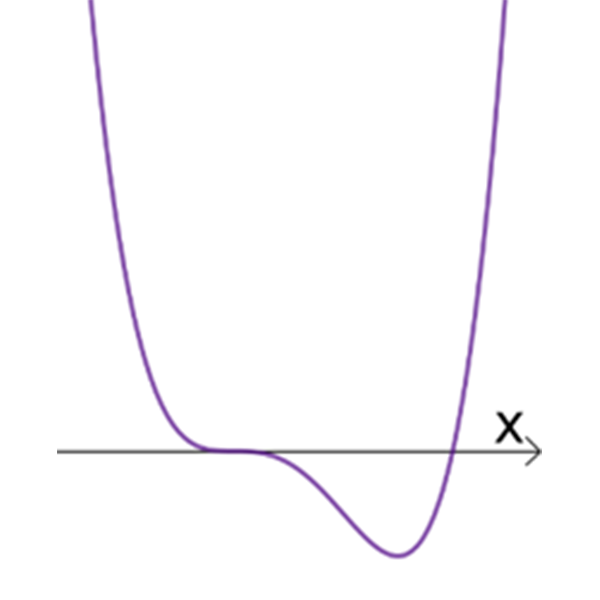
III
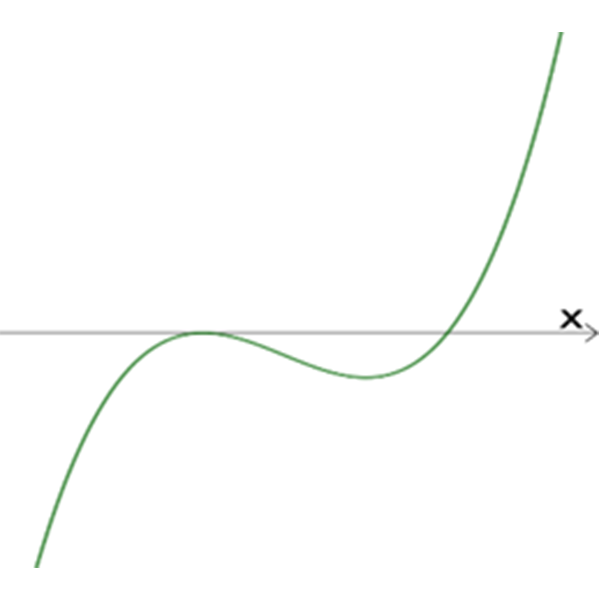
IV
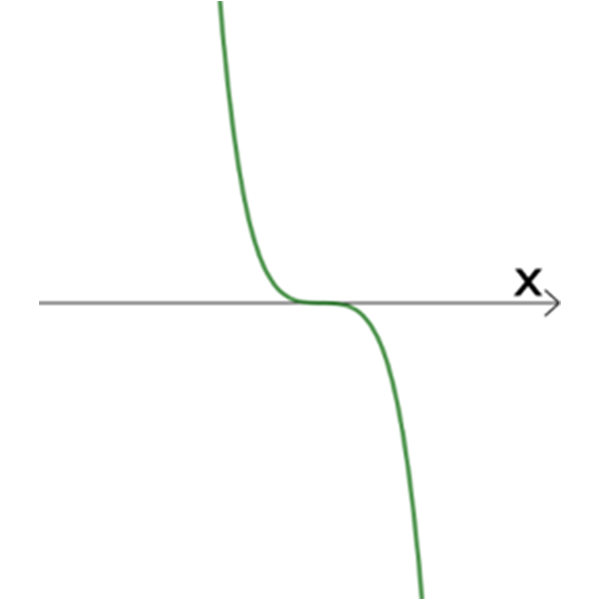
V
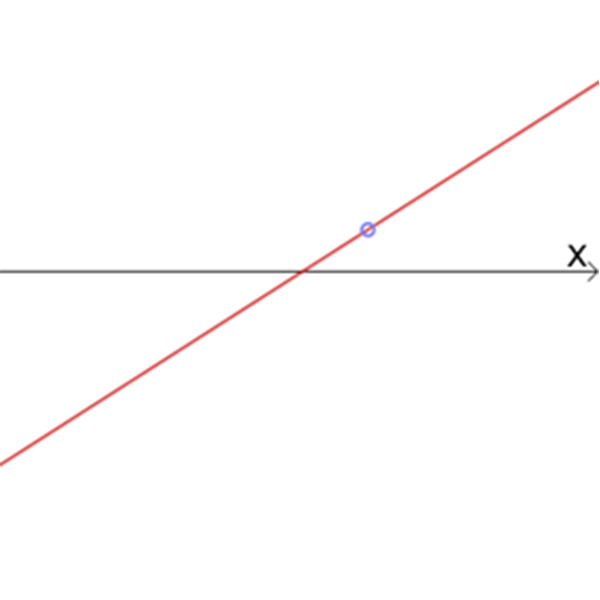
VI
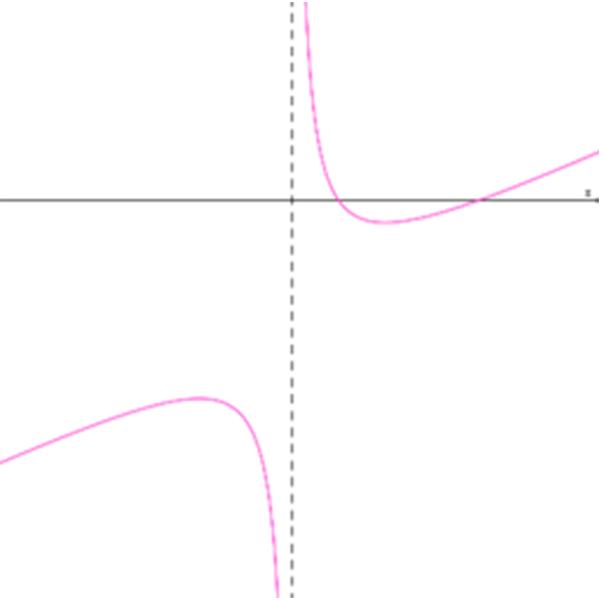
- לפניכם, בטבלה למטה, רשומים מאפיינים של הפונקציה ההופכית \(\Large\frac {1}{h_{n}{(x)}}\).
התאימו בין המאפיינים של הפונקציה ההופכית לבין הביטויים של הפונקציות \(h_{n}{(x)}\).
שימו לב: למאפיין של פונקציה הופכית יכולים להתאים כמה ביטויים של פונקציות, וכן יכולים להיות ביטויים של פונקציות שאין להם התאמה מבין המאפיינים הנתונים.
מאפיינים של הפונקציה ההופכית
א. לפונקציה ההופכית אין אסימפטוטות אנכיות.
ב. לפונקציה ההופכית יש יותר מאסימפטוטה אנכית אחת.
ג. מספר נקודות הקיצון של הפונקציה \(h_{n}{(x)}\) שווה למספר נקודות הקיצון של הפונקציה ההופכית שלה \(\Large\frac {1}{h_{n}{(x)}}\).
ד. הפונקציה ההופכית חיובית בכל תחום הגדרתה.
ה. לפונקציה ההופכית אין נקודות קיצון.
ו. ייתכן שהפונקציה \(h_{n}{(x)}\) והפונקציה ההופכית שלה \(\Large\frac {1}{h_{n}{(x)}}\) לא נחתכות ביניהן.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















