הקשר בין גרף פונקציה לגרף הנגזרת שלה – המקרה של פולינום
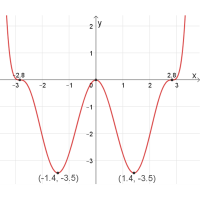
נקודות חיתוך של \(f(x)\) עם הצירים:
\((2.8 ,0)\) , \((0 ,0)\) , \((-2.8 ,0)\)
נקודות קיצון: מקסימום: \((0 ,0)\) מינימום: \((1.4 ,-3.5)\) , \((-1.4 ,-3.5)\)
נקודות פיתול: \((2.8 ,0)\) , \((-2.8 ,0)\)
מטרתכם: לסרטט סקיצה לגרף הנגזרת \(f'{(x)}\), עבור הפונקציה הנתונה באיור.
תנו דעתכם לתחומי החיוביות והשליליות של הנגזרת ולנקודות הקיצון שלה.
תוכלו להיעזר ביישומון.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- כאשר גוררים את הנקודה האדומה, המסומנת על הגרף, ניתן לראות כיצד נע איתה המשיק לגרף הפונקציה, וכך לחזות בשיפועיו המשתנים.
- מתוך מחסן הנקודות יש לגרור נקודות למקומות המתאימים להן לתאור הפונקציה המבוקשת.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה המבוקשת. - ניתן לבצע בדיקה לקבלת משוב.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.