חזקה טבעית של פונקציה - חלק א' - חזקה שניה \(f^2{(x)}\)
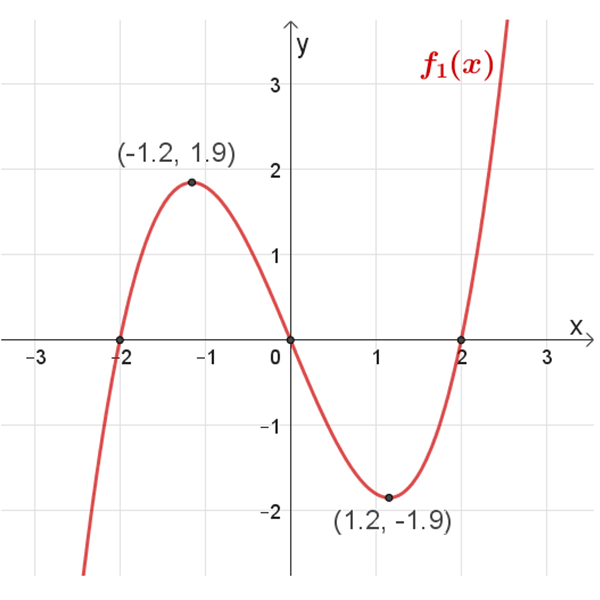
\(f_1(x)\)
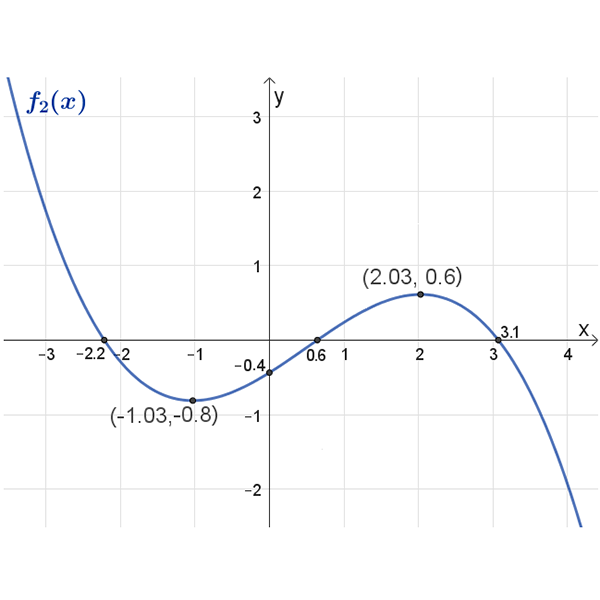
\(f_2(x)\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((2,0)\) , \((0 , 0)\) , \((-2,0)\)
נקודות קיצון: מקסימום \((-1.2,1.9)\) , מינימום \((1.2, -1.9)\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((0,3.1)\) , \((0.6,0)\) , \((0,-0.4)\) , \((-2.2,0)\)
נקודות קיצון: מקסימום: \((2.03,0.6)\) , מינימום \((-1.03,-0.8)\)
שימו לב גם לנקודות החיתוך בין \(f_n(x)\) ל-\(f_n\space^2(x)\) ולמצב ההדדי ביניהן.
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
סעיף ב
\(f(x)\)היא פונקציית פולינום כלשהו.
אילו קשרים מצאתם שקיימים בין גרף הפונקציה \(f(x)\) לבין גרף הפונקציה \(f^2(x)\)? נמקו תשובתכם.
תוכלו לבדוק קשרים בין \(f_n(x)\) ל-\(f_n\space^2(x)\) עבור פונקציות נוספות בעזרת היישומון הדינאמי המצורף.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- כדי לעבור לפונקציה האחרת יש ללחוץ על שנה פונקציה, הכפתור הצהוב, בתפריט שבתחתית היישומון.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
- ניתן להזיז את הפולינום הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים)