שיקופים וערך מוחלט של פונקציה - חלק ב'
\(f_1{(x)}\)
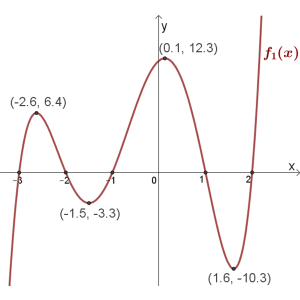
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((2,0)\) , \((1,0)\) , \((0,12)\) , \((-1,0)\) , \((-2,0)\) , \((-3,0)\)
נקודות קיצון: מקסימום \((0.1,12.3)\) , \((-2.6,6.4)\) ,מינימום \((1.6,-10.3)\) , \((-1.5,-3.3)\)
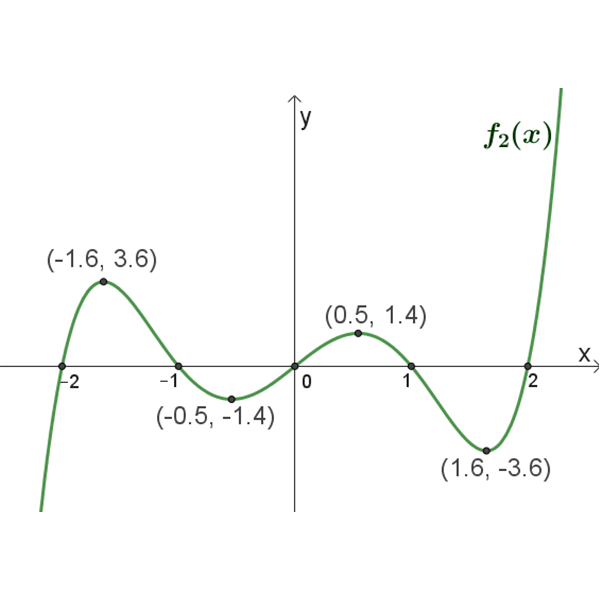
\(f_2{(x)}\)
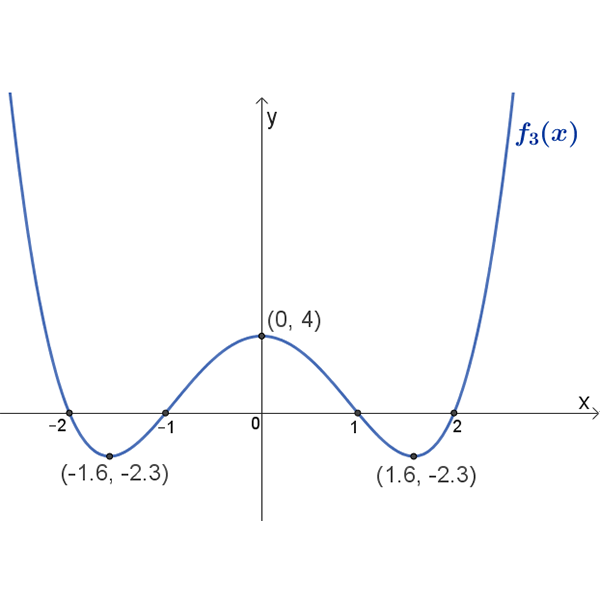
\(f_3{(x)}\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((2,0)\) , \((1,0)\) , \((0,0)\) , \((-1,0)\) , \((-2,0)\)
נקודות קיצון: מקסימום \((0.5,1.4)\) , \((-1.6,3.6)\) מינימום \((1.6,-3.6)\) , \((-0.5,-1.4)\)
תחום הגדרה: כל \(x\)
נקודות החיתוך עם הצירים: \((2,0)\) , \((1,0)\) , \((0,4)\) , \((-1,0)\) , \((-2,0)\)
נקודות קיצון: מקסימום \((0,4)\) מינימום \((1.6,2.3)\) , \((-1.6,-2.3)\)
- סרטטו, עבור כל אחת מהפונקציות (במערכת הצירים שלה), את גרף הפונקציה \(f_n(-x)\)
תוכלו לסרטט את הגרפים ולבדוק תשובותיכם בעזרת היישומון המצורף.
- \(h(x)\) היא פונקציית פולינום כלשהו.
מצאו ותארו את הקשרים בין גרף הפונקציה \(h(x)\) לבין גרף הפונקציה \(h(-x)\).
נמקו מדוע מתקיים כל אחד מהקשרים שמצאתם.
בתשובתכם, תוכלו להיעזר במושגים הבאים (לא בהכרח בכולם):
נקודות אפס, נקודות קיצון וסוגן, תחומי עליה וירידה, תחומי חיוביות ושליליות, שיקוף בציר x, שיקוף בציר y, פונקציה זוגית, פונקציה אי-זוגית, פונקציה חיובית, פונקציה שלילית, פונקציה אי-חיובית, פונקציה אי-שלילית, מספרים נגדיים.
תוכלו להיעזר ביישומון דינאמי כדי לבדוק את הקשרים בין הפונקציות: \(h(x)\) , \(h(-x)\) עבור פונקציות רבות.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- כדי לעבור לפונקציה האחרת יש ללחוץ על שנה פונקציה, בכפתור הצהוב בתפריט שבתחתית היישומון.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- כדי לעבור לפונקציה האחרת יש ללחוץ על שנה פונקציה, בכפתור הצהוב בתפריט שבתחתית היישומון.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
- ניתן להזיז את הפולינום הזזה אופקית ואנכית בעזרת גרירת הנקודה האדומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים)