משפט תלמי
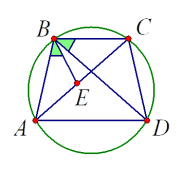
ונתון כי: \(\measuredangle CBD=\measuredangle ABE\).
- הוכיחו כי: \(\measuredangle BEC=\measuredangle DAB\).
- הוכיחו כי: \(AB \cdot DC + AD \cdot BC= DB \cdot AC\)
תוכלו להיעזר ביישומון.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.





















