נקודת מפגש התיכונים וחותכים אחרים - הוכחות באמצעות שטחים
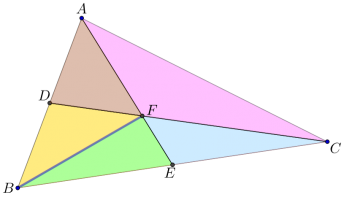
סעיף א
הסבירו מדוע המשולשים בכל זוג מהבאים שווים בשטחם:
\(ABE\) ו- \(AEC\)
\(ADF\) ו- \(DBF\)
\(BFE\) ו- \(CFE\)
\(BDC\) ו- \(ADC\)
סעיף ב
סמנו: \(S_{BDF}=S_1\) , \(S_{BFE}=S_2\)
- בטאו את \(S_{AFC}\) באמצעות \(S_1\)
- בטאו את \(S_{AFC}\) באמצעות \(S_2\)
סעיף ג
הוכיחו: \(AF:FE=2:1\).
סעיף ד
הסיקו את המשפט השלם בדבר מפגש התיכונים:
- נקודת המפגש של כל שני תיכונים מחלקת כל אחד מהם ביחס 2:1, כך שהחלק הארוך קרוב לקודקוד.
- בכל משולש שלושת התיכונים נפגשים בנקודה אחת.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















