נקודת מפגש התיכונים וחותכים אחרים - הוכחות באמצעות שטחים
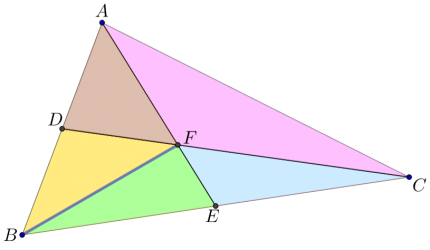
- בטאו באמצעות \(n\) את היחס בו מחלקת הנקודה \(F\) את הקטעים \(AE\) ו- \(CD\).
- הוכיחו כי הנקודה \(F\) נמצאת על התיכון מהנקודה \(B\).
- הסיקו מהנ"ל כי: שלושת התיכונים במשולש נפגשים בנקודה אחת, ונקודה זו מחלקת כל תיכון ביחס 2:1, כך שהחלק הארוך קרוב לקודקוד.
- תוכלו לעבור לבעיית האתגר.
- מידת הצורך פתרו את הבעיות במדרגה 1.





















