גבהים במשולש וחוצי זוויות - למורה
החומר הנלמד:
תרגול השימוש במושגים ובמשפטים הקשורים למעגלים חוסמים מרובעים, זוויות היקפיות שוות, זוויות היקפיות ישרות ודמיון משולשים ישרי זווית.
כיתה:
כיתה י' / כיתה י"א
אבחון המשימה:
במשימה מוכיחים תכונה מעניינת של גבהים במשולש: נקודת המפגש של הגבהים במשולש חד-זווית מתלכדת עם נקודת המפגש של חוצי הזוויות של המשולש שקודקודיו הם עקבי הגבהים.
במשולש קהה זווית מפגש חוצי הזוויות של המשולש שקודקודיו הם עקבי הגבהים מתלכדת עם קודקוד הזווית הקהה. אמנם אין תכונה זו נכללת ברשימת המשפטים להוכחה, אך העיסוק בה נוגע במספר משפטים חשובים ומתרגל התייחסות למעגלים חוסמים מרובעים, לזוויות היקפיות ישרות, לזוויות היקפיות אחרות הנשענות על אותה קשת ולדמיון משולשים.
מבנה המשימה:
בעיית מטרה אחת, ושלוש מדרגות בשילוב יישומונים בגיאוגברה.
ידע קודם:
המשפטים הקשורים למושגים: מרובעים ברי חסימה במעגל, זוויות היקפיות, דמיון משולשים.
מטרות לימודיות:
- זיהוי מרובעים ברי חסימה לפי:
- לפי סכום זוויות נגדיות 180 מעלות,
- לפי קטע עליו נשענות שתי זוויות ישרות.
- תרגול זיהוי של זוויות היקפיות שוות שנשענות על קשת אחת בממעגלים שחוסמים מרובעים.
- תרגול זיהוי משולשים דומים
משימת המטרה:
הוכחת התכונה: נקודת המפגש של הגבהים במשולש חד-זווית מתלכדת עם נקודת המפגש של חוצי הזוויות של המשולש שקודקודיו הם עקבי הגבהים.
מדרגה 1:
יש למצוא מרובעים ברי חסימה במשולש חד זוויות בו מסומנים הגבהים וחוצי הזוויות.
מדרגה 2:
בסרטוט דומה לזה שמופיע במדרגה 1 בצירוף סימונים בצבעים של זוויות וסרטוט מעגלים יש למצוא מרובעים ברי חסימה ומשולשים דומים.
מדרגה 3:
באותו סרטוט כמו במדרגה 2 נתונים מרובעים ברי חסימה, יש לאתר זוויות השוות לזווית נתונה ומרובעים נוספים ברי חסימה.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות, ברמה המתאימה. מומלץ להיעזר ביישומונים בגיאוגברה, שמאפשרים חיפוש של מרובעים ברי חסימה ומדידת זוויות.
המשימה מתאימה להפעלה בשלבי תרגול מתקדמים של הגיאומטריה האוקלידית, במיוחד לקראת בחינת הבגרות.
בסיום המשימה יש לערוך דיון בבעיית המטרה.
שימוש ביישומונים:
בכל השלבים ישנם יישומונים.
שיעורי בית:
סיום המשימה.
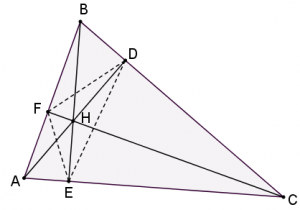
- הוכיחו כי הגבהים במשולש \(\triangle ABC\) חוצים את זוויות המשולש \(\triangle DEF\).
- גלו: היכן נמצאת נקודת המפגש של חוצי הזוויות של המשולש שקודקודיו בעקבי הגבהים כאשר המשולש אינו חד-זווית?
- במידת הצורך פתרו את הבעיות במדרגה 1.
- בגרירת כל אחת מהנקודות הכחולות (\(A\) , \(B\) , \(C\)), ניתן לשנות את צורת המשולש.

מצאו את המרובעים ברי החסימה במעגל. כמה מצאתם?
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
בגרירת כל אחת מהנקודות הכחולות (\(A\) , \(B\) , \(C\)), ניתן לשנות את צורת המשולש.
בגרירת כל אחת מהנקודות הכחולות (\(A\) , \(B\) , \(C\)), ניתן לשנות את צורת המשולש.
- מצאו את הזוגות / השלשות / הרביעיות של משולשים דומים באיור.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
בגרירת כל אחת מהנקודות הכחולות (\(A\) , \(B\) , \(C\)), ניתן לשנות את צורת המשולש.
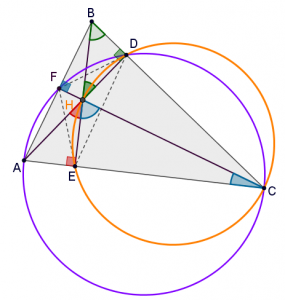
- מצאו את כל הזוויות השוות ל- \(\measuredangle{FCE}\)
- מצאו מרובעים נוספים ברי חסימה במעגל.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
בגרירת כל אחת מהנקודות הכחולות (\(A\) , \(B\) , \(C\)), ניתן לשנות את צורת המשולש.





















