הגדרת מקומות גיאומטריים באמצעות מספרים מרוכבים - למורה
חומר לימוד:
הגדרת מקומות גיאומטריים באמצעות מספרים מרוכבים.
המשימה מתאימה לתרגול מתפתח ומתקדם של הגדרת חלקי מישור באמצעות אי-שוויונות במספרים מרוכבים.
כיתה:
כיתה י"ב
מבנה המשימה:
בעיית מטרה ושלוש מדרגות.
ידע קודם:
שימוש במושגים: \(|z|\) , \(Arg(z)\) , \(Im(z)\) , \(Re(z)\) , \(|z-a|\) (\(a\) מספר מרוכב) לצורך הגדרת פנים וחוץ של מעגלים, גזרות, חצאי מישור וכד'.
מטרות לימודיות:
תרגול התייחסות למישור כמקום גיאומטרי של מספרים מרוכבים ותרגול הקשרים בין המושגים שהוזכרו לעיל.
משימת המטרה:
בבעיה סרטוט מורכב (לא מרוכב!)
מדרגה 1:
בבעיה סרטוט פרח מארבעה מעגלים.
מדרגה 2:
בבעיה סרטוט מעגל, גזרות וחצאי מישור.
מדרגה 3:
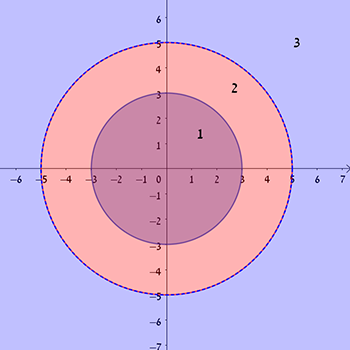
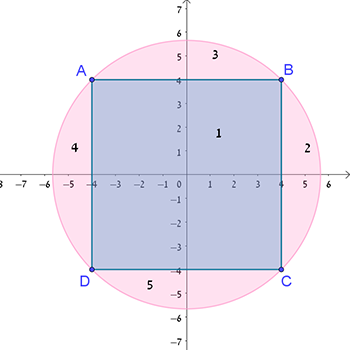
שתי בעיות. האחת עוסקת בטבעת והשניה בריבוע בתוך עיגול.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות. המורה יציג את בעיית המטרה. התלמיד יכול לבחור לפי איזו רמה ברצונו לעבוד.
שימוש ביישומונים:
אין
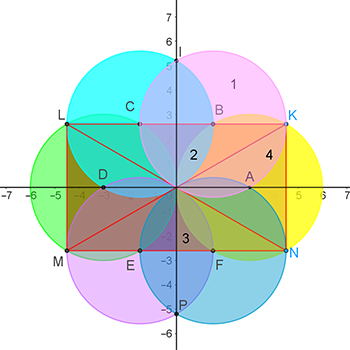
1 – השטח הצבוע בוורוד, שמחוץ לעיגול הצהוב והעיגול התכלת,
2 – השטח המשותף לעיגול התכלת ולעיגול הצהוב,
3 – השטח במלבן \(KLMN\), מימין לציר ה-\(y\), ומחוץ לעיגול הצהוב,
4 – השטח המשותף למשולש \(KON\), ולעיגול הורוד ומחוץ לעיגול הכחול, (\(O\) ראשית הצירים)
תוכלו להגדיר שטחים נוספים כרצונכם.
שימו לב: כל המעגלים עוברים בראשית הצירים, מרכזי המעגלים: \(A\) , \(B\) , \(C\) , \(D\) , \(E\) , \(F\) מתאימים לשישה שורשים שונים של מספר מרוכב. רדיוס כל מעגל הוא: 3 יחידות אורך. הנקודות \(K\) , \(L\) , \(M\) , \(N\) הן נקודות חיתוך בין מעגלים, כמתואר בסרטוט.
- במידת הצורך פתרו את הבעיות במדרגה 1.
סעיף ב
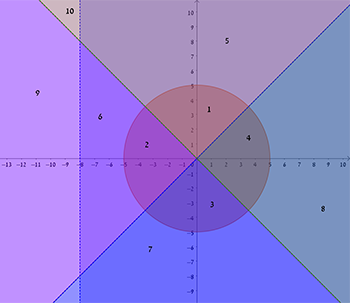
השתמשו בתכונות של מספרים מרוכבים ובמושגים: \(z|\) , \(Arg(z)\) , \(Im(z)\) , \(Re(z)\), והגדירו באמצעותם את השטחים השונים (5 במספר) אשר בסרטוט שלפניכם (כל שטח צבוע בצבע שונה – הצירים לא מפרידים בין השטחים). המרובע \(ABCD\) הוא ריבוע.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.