קשרים בין פונקציה \(f{(x)}\) לפונקציה ההופכית לה \(\frac {1}{f{(x)}}\) - חלק א' - למורה
חומר לימוד:
סרטוט הגרף של הפונקציה \(\Large\frac{1}{f{(x)}}\) כאשר נתון הגרף של הפונקציה \(f{(x)}\). התחלת הוראת הנושא, זאת לאחר הכרת הפרבולה.
כיתה:
כיתה י' או כיתה י"א, כשלומדים על פונקציות מנה של פולינומים.
מבנה המשימה:
בעיית מטרה ושלוש בעיות מדרגה. לכל הבעיות ישנם יישומונים.
ידע קודם:
- הכרת הפונקציה: \(y=1/x\) והזזות ומתיחות שלה
- הכרת פולינומים מסוגים שונים
- תכונות של פונקציה כמו: תחום הגדרה, נקודות חיתוך עם הצירים, נקודות קיצון וסוגן, תחומי עליה וירידה, אסימפטוטות מקבילות לצירים, תחומי חיוביות ושליליות, נקודות חיתוך בין פונקציות
מטרות לימודיות:
- הכרת קשרים בין תכונות הפונקציה \(f{(x)}\) לבין הפונקציה ההופכית לה \(\Large\frac{1}{f{(x)}}\) , ניתן להגיע לקשרים אלו ללא הנגזרת הכללית של \(\Large\frac{1}{f{(x)}}\) אלא על סמך תכונות של מספרים
- אפיון נקודות חיתוך בין \(f{(x)}\) ל- \(\Large\frac{1}{f{(x)}}\)
- הבנת המצב ההדדי בין הגרפים של הפונקציות \(f{(x)}\) ו- \(\Large\frac{1}{f{(x)}}\)
סוג הדירוג:
משימת המטרה:
בבעיית המטרה לפונקציה יש שלוש נקודות קיצון, אחת מהן משיקה לציר ה- \(x\), ושתי נקודות חיתוך נוספות עם ציר ה-\(x\).
מדרגה 1:
שתי פונקציות: לאחת שתי נקודות קיצון, אסימפטוטה אופקית, והיא חיובית לכל \(x\). לשנייה נקודת קיצון אחת, שתי נקודות חיתוך עם ציר \(x\) ואסימפטוטה אופקית אחת.
מדרגה 2:
שתי פרבולות: אחת חיובית לכל \(x\) ואחת בעלת מקסימום ושתי נקודות חיתוך עם ציר ה-\(x\).
מדרגה 3:
שלוש פרבולות – על התלמיד לבחור את הגרפים המתאימים לפונקציות ההופכיות להן מתוך גרפים נתונים.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. תלמידים המסיימים לפתור את בעיית המטרה בהקדם וללא עזרת בעיות המדרגה, ניתן להפנות אותם לפתור את בעיות המדרגה.
שימוש ביישומונים:
לבעיית המטרה ולכל בעיות המדרגות יש יישומונים מתאימים.
שיעורי בית:
תלמידים שלא הספיקו לסיים את בעיית המטרה בכיתה, ימשיכו בבית.
משימות מומלצות:
למשימה זו שתי משימות המשך – פונקציה הופכית חלק ב' וחלק ג' – אותן ניתן לשלב בכל שלב בהוראה, לאחר הפעלת חלק א', כשיעורי בית, הפעלה בכיתה, או כהכנה לקראת בחינה.
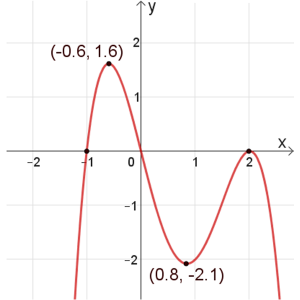
תחום ההגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((2,0)\) , \((0,0)\) , \((-1,0)\)
נקודות קיצון: מקסימום: \((2,0)\) , \((-0.6,1.6)\) , מינימום: \((0.8,-2.1)\)
- סרטטו באותה מערכת צירים את גרף הפונקציה ההופכית \(\Large\frac{1}{f{(x)}}\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף. - מצאו קשרים בין גרף הפונקציה \(f{(x)}\) לבין גרף הפונקציה \(\Large\frac{1}{f{(x)}}\).
- נמקו מדוע מתקיים כל אחד מהקשרים שמצאתם.
תוכלו לבדוק תשובותיכם בעזרת היישומונים המצורפים.
אם טעיתם חישבו ממה נבעה הטעות.
- במידת הצורך, פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה האדומה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.
- ניתן להזיז את הפולינום הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים)
א – \(f_{1}(x)\)
ב – \(f_{2}(x)\)
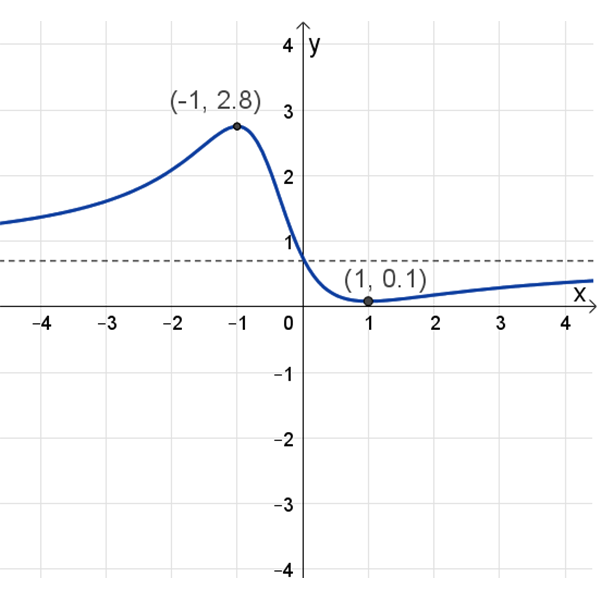
תחום ההגדרה: כל \(x\)
נקודת חיתוך עם הצירים: \((0,0.75)\)
נקודות קיצון: מקסימום: \((-1,2.8)\) , מינימום: \((1,0.1)\)
אסימפטוטה אופקית: \(y=0.75\)
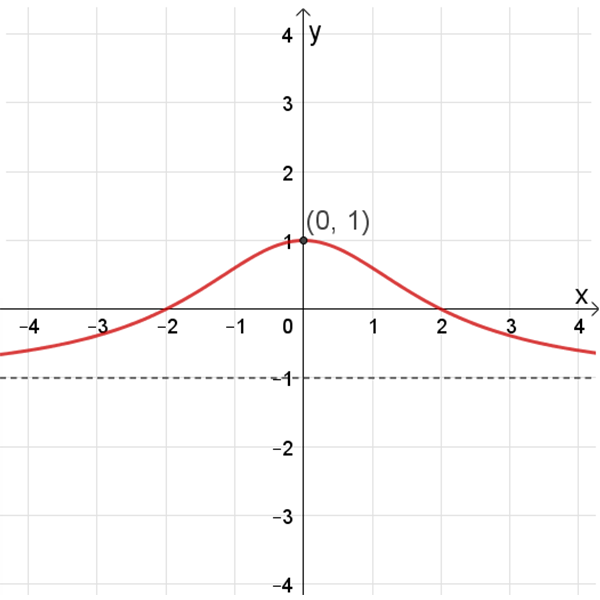
תחום ההגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((2,0)\) , \((0,1)\) , \((-2,0)\)
נקודת קיצון: מקסימום: \((0,1)\)
אסימפטוטה אופקית: \(y=-1\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
א – \(f_{1}(x)\)
ב – \(f_{2}(x)\)
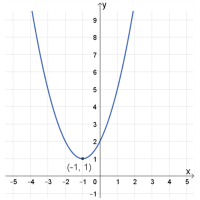
תחום ההגדרה: כל \(x\)
נקודת חיתוך עם הצירים: \((0,2)\)
נקודת קיצון: מינימום: \((-1,1)\)
תחום ההגדרה: כל \(x\)
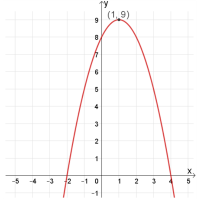
נקודות חיתוך עם הצירים: \((4,0)\) , \((0,8)\) , \((-2,0)\)
נקודת קיצון: מקסימום: \((1,9)\)
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
גרפים של פונקציות נתונות:
פונקציה א
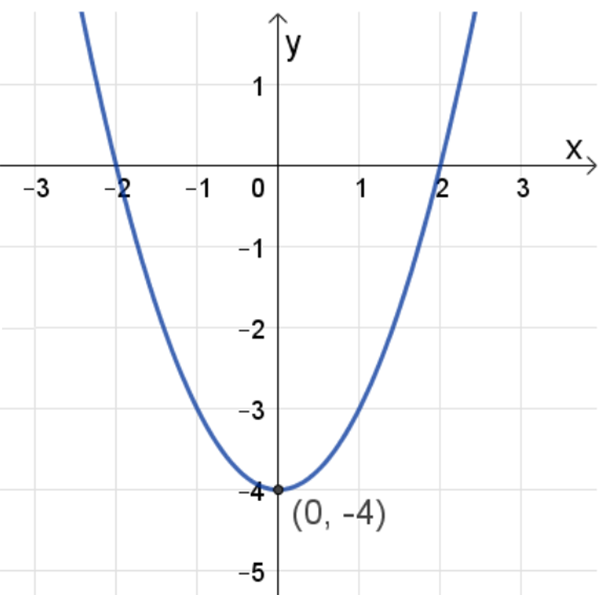
פונקציה ב
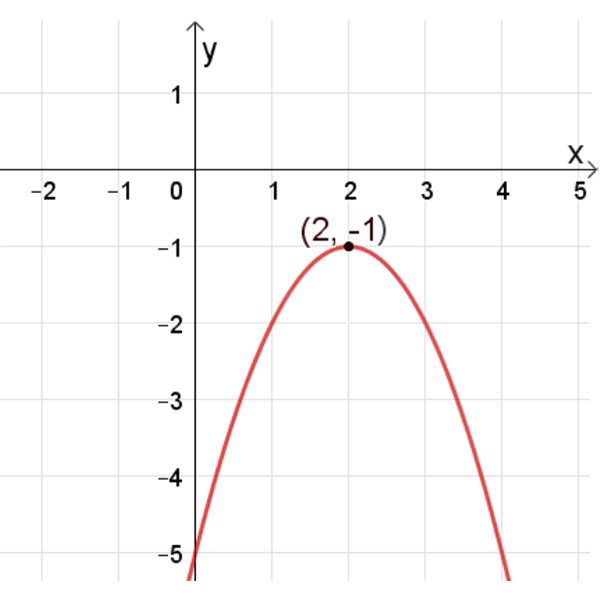
פונקציה ג
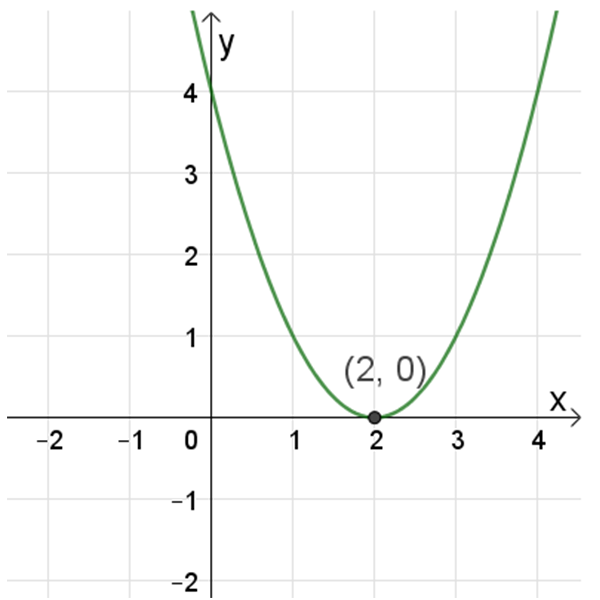
גרפים של פונקציות הופכיות:
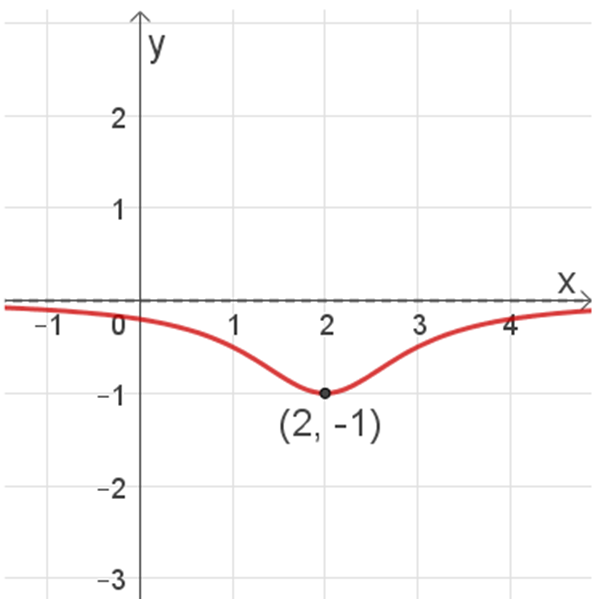
פונקציה I
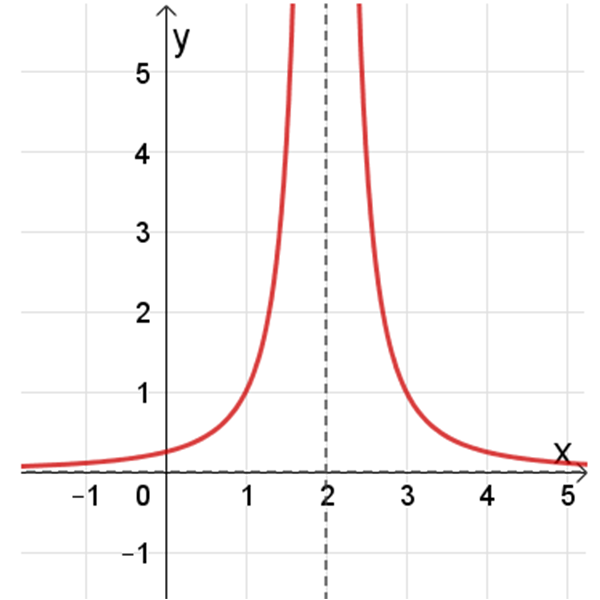
פונקציה II
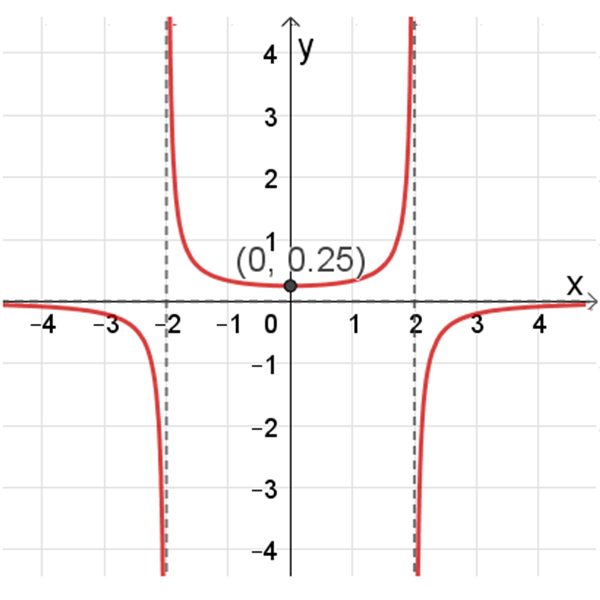
פונקציה III
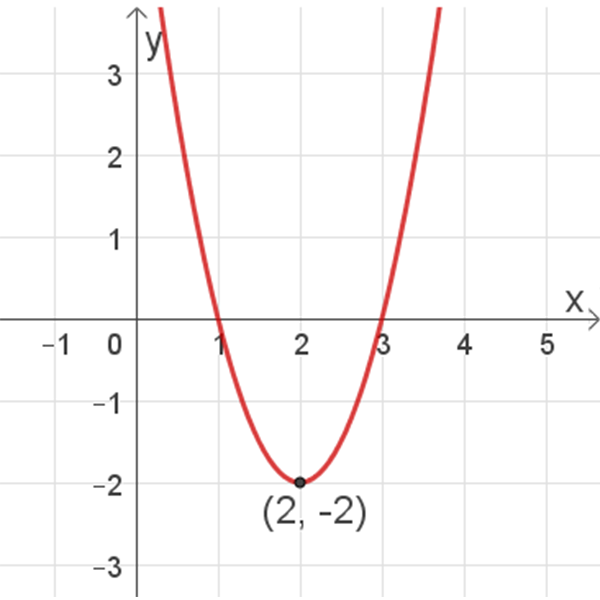
פונקציה IV
פונקציה V
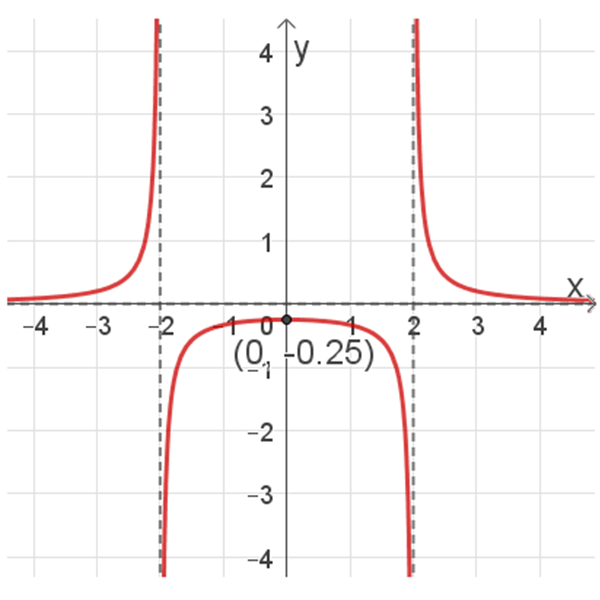
פונקציה VI
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה האדומה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.