קשרים בין פונקציה \(f{(x)}\) לפונקציה ההופכית לה \(\frac {1}{f{(x)}}\) - חלק ב' - למורה
חומר לימוד:
סרטוט הגרף של הפונקציה \(\Large\frac{1}{f{(x)}}\) כאשר נתון הגרף של הפונקציה \(f{(x)}\) בשילוב שיקופים והזזות של הפונקציה ההופכית.
כדאי להפעיל את המשימה לאחר הפעלת המשימה קשרים בין פונקציה \(f{(x)}\) לבין הפונקציה ההופכית לה \(\Large\frac{1}{f{(x)}}\) חלק א'.
כיתה:
כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות. מצורפים יישומונים.
ידע קודם:
- סרטוט הגרף של הפונקציה \(\Large\frac{1}{f{(x)}}\) כאשר נתון הגרף של הפונקציה \(f{(x)}\)
- תכונות של פונקציה כמו: תחום הגדרה, נקודות חיתוך עם הצירים, נקודות קיצון וסוגן, תחומי עליה וירידה, אסימפטוטות מקבילות לצירים, תחומי חיוביות ושליליות.
- הזזות ושיקופים של פונקציות
מטרות לימודיות:
- הכרת קשרים בין תכונות פונקציה \(f{(x)}\) לבין תכונות הפונקציה ההופכית לה \(\Large\frac{1}{f{(x)}}\).
- מענה לשאלה: אילו תכונות של הפונקציה \(\Large\frac{1}{f{(x)}}\) משתנות ואילו לא משתנות כתוצאה מפעולות עליה כמו: הזזות ושיקופים.
סוג הדירוג:
משימת המטרה:
בבעיית המטרה לפונקציה הנתונה יש שתי נקודות קיצון, שלוש נקודות חיתוך עם ציר ה-\(x\), ושאלה משולבים שני פרמטרים.
מדרגה 1:
לפונקציה הנתונה שתי נקודות קיצון אחת מהן על ציר ה-\(x\), שתי נקודות חיתוך עם ציר \(x\), בשאלה משולב פרמטר אחד.
מדרגה 2:
נתונה אותה פונקציה כמו במדרגה 1, בשאלה לא משולבים פרמטרים.
מדרגה 3:
נתונה פרבולה, בשאלה לא משולבים פרמטרים.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. רצוי להיעזר ביישומונים המצורפים.
שימוש ביישומונים:
בכל בעייה ובכל שלב השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה והגיע למסקנות הנדרשות. אם תלמיד טעה / לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
שיעורי בית:
סיום המשימה
הערה:
ניתן לשלב משימה זו בכל שלב בהוראה, לאחר הפעלת חלק א', כשיעורי בית, הפעלה בכיתה, או כהכנה לקראת בחינה. בכל מקרה רצוי לקיים דיון כיתתי על השאלות שמופיעות במשימה.
למשימה זו קיימת משימת המשך: פונקציה הופכית – חלק ג'.
משימות מומלצות:
- למשימה זו קיימת משימת קדם – פונקציה הופכית – חלק א'.
- למשימה זו קיימת משימת המשך – פונקציה הופכית – חלק ג'.
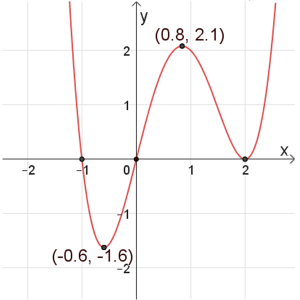
נקודות חיתוך עם הצירים: \((2 ,0)\) , \((0 ,0)\) , \((-1 ,0)\)
נקודות קיצון: מקסימום: \((0.8 ,2.1)\) , מינימום: \((2,0)\) , \((-0.6,-1.6)\)
סעיף א
- סרטטו סקיצה כללית של גרף הפונקציה \(\Large\frac{1}{f{(x+c)}
}\normalsize+k\).
\(1<k<4\) , \(0<c<1.5\)
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף. - בטאו בעזרת \(k\) ו-\(c\) (במידת הצורך) את שיעורי נקודות הקיצון ואת האסימפטוטות המקבילות לצירים של הפונקציה: \(\Large\frac{1}{f{(x+c)}}\normalsize+k\).
סעיף ב
- סרטטו סקיצה כללית של גרף הפונקציה: \(\Large\frac{1}{f{(-x)}}\normalsize-k\) עבור \(k>2\)
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף. - בטאו בעזרת \(k\) (במידת הצורך) את שיעורי נקודות הקיצון ואת האסימפטוטות המקבילות לצירים של הפונקציה: \(\Large\frac{1}{f{(-x)}}\normalsize-k\)
- במידת הצורך, פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם נקודות במקומות המתאימים להן.
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה הכתומה שעל הקווים האנכיים/אופקיים המקווקווים, אל המיקום המתאים.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לשנות את הפונקציה על-ידי שינוי הערכים \(a\) , \(b\) , \(c\) , \(d\) , \(k\), וכן לבחור בהצגת פונקציות נוספות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
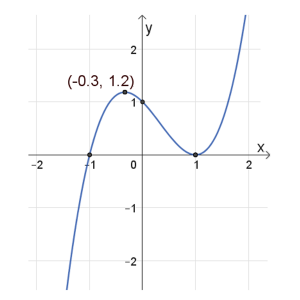
נקודות חיתוך עם הצירים: \((1 ,0)\) , \((0 ,1)\) , \((-1 ,0)\)
נקודות קיצון: מקסימום \((-0.3 ,1.2)\) , מינימום \((1 ,0)\).
סעיף א
- סרטטו סקיצה כללית של גרף הפונקציה \(\Large\frac{1}{g{(x+c)}
}\normalsize-2\) עבור \(0<c<1\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף. - בטאו בעזרת \(c\) (במידת הצורך) את שיעורי נקודות הקיצון ואת האסימפטוטות המקבילות לצירים של הפונקציה: \(\Large\frac{1}{g{(x+c)}}\normalsize-2\).
סעיף ב
- סרטטו את גרף הפונקציה: \(\Large\frac{1}{g{(-x)}}\normalsize+2\).
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף. - מצאו מה הם שיעורי נקודות הקיצון ומה הן האסימפטוטות המקבילות לצירים של הפונקציה: \(\Large\frac{1}{g{(-x)}}\normalsize+2\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- מתוך מחסן הנקודות יש לגרור ולמקם נקודות במקומות המתאימים להן.
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה הכתומה שעל הקווים האנכיים/אופקיים המקווקווים, אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לשנות את הפונקציה על-ידי שינוי הערכים \(a\) , \(b\) , \(c\) , \(d\) , \(k\), וכן לבחור בהצגת פונקציות נוספות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
נקודות חיתוך עם הצירים: \((1 ,0)\) , \((0 ,1)\) , \((-1 ,0)\)
נקודות קיצון: מקסימום \((-0.3 ,1.2)\) , מינימום \((1 ,0)\).
סעיף א
- סרטטו סקיצה כללית של גרף הפונקציה: \(\Large\frac{1}{g{(x-1)}}\normalsize-2\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף. - מצאו מה הם שיעורי נקודות הקיצון ומה הן האסימפטוטות המקבילות לצירים של הפונקציה: \(\Large\frac{1}{g{(x-1)}}\normalsize-2\).
סעיף ב
- סרטטו את גרף הפונקציה: \(\Large\frac{1}{g{(-x)}}\).
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף. - מצאו מה הם שיעורי נקודות הקיצון ומה הן האסימפטוטות המקבילות לצירים של הפונקציה: \(\Large\frac{1}{g{(-x)}}\)
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- מתוך מחסן הנקודות יש לגרור ולמקם נקודות במקומות המתאימים להן.
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה הכתומה שעל הקווים האנכיים/אופקיים המקווקווים, אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לשנות את הפונקציה על-ידי שינוי הערכים \(a\) , \(b\) , \(c\) , \(d\) , \(k\), וכן לבחור בהצגת פונקציות נוספות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
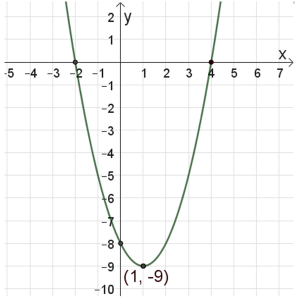
נקודות החיתוך של הפונקציה עם הצירים הן: \((4 ,0)\) , \((0 ,-8)\) , \((-2 ,0)\).
נקודת קיצון: מינימום \((1,-9)\).
- סרטטו את גרף הפונקציה: \(\Large\frac{1}{h{(x+1)}}\).
- סרטטו את גרף הפונקציה: \(\Large\frac{1}{h{(x+1)}}\normalsize+3\).
- סרטטו את גרף הפונקציה: \(\Large\frac{1}{h{(-x)}}\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- מתוך מחסן הנקודות יש לגרור ולמקם נקודות במקומות המתאימים להן.
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה הכתומה שעל הקווים האנכיים/אופקיים המקווקווים, אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לשנות את הפונקציה על-ידי שינוי הערכים \(a\) , \(b\) , \(c\) , \(d\) , \(k\), וכן לבחור בהצגת פונקציות נוספות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.