קשרים בין פונקציה \(f{(x)}\) לפונקציה ההופכית לה \(\frac {1}{f{(x)}}\) - חלק ג' - למורה
חומר לימוד:
הקשר בין מאפייני הפונקציה \(\large\frac {1}{f{(x)}}\) לבין הביטוי האלגברי של הפונקציה \(f{(x)}\) לבין גרף הפונקציה \(f{(x)}\). המשימה מתאימה להפעלה לאחר הוראת הנושא של הקשר בין גרף הפונקציה לבין גרף הפונקציה ההופכית \(\large\frac {1}{f{(x)}}\).
כיתה:
כיתה י"א
מבנה המשימה:
בעיית מטרה אחת ושלוש מדרגות. מצורפים יישומונים.
ידע קודם:
- הכרת פולינומים מסוגים שונים
- הכרת פונקציות מנה
- הכרת תכונות של פונקציה כמו: תחום הגדרה, נקודות חיתוך עם הצירים, נקודות קיצון וסוגן, תחומי עליה וירידה, אסימפטוטות מקבילות לצירים, אי-רציפות סליקה, תחומי חיוביות ושליליות, נקודות חיתוך בין פונקציות.
מטרות לימודיות:
זיהוי והבנה של קשרים בין תכונות ביטוי אלגברי של פונקציה \(f{(x)}\) לבין הגרף שלה, וכן זיהוי והבנה של הקשרים הקיימים בין תכונות הפונקציה \(f{(x)}\) לבין תכונות הפונקציה ההופכית.
משימת המטרה:
במשימת המטרה יש להתאים בין מאפיינים של גרפים לבין ביטויים של פונקציות מכפלה ומנה. לפתרון המשימה אין צורך בחקירה מלאה של כל אחת מחמש מהפונקציות.
ניתן לסרטט סקיצה של הפונקציות, שהביטוי שלהן נתון, על פי נקודות האפס של כל אחת מהן, ותחומי חיוביות ושליליות שלהן, על פי סקיצות אלה ניתן לדעת את מספר נקודות הקיצון, אך לא את שיעוריהן המדויקים (מלבד במקרים מיוחדים בהן נקודת הקיצון נמצאת על ציר ה- \(x\)).
מדרגה 1:
נתונים ביטויים של שלוש פונקציות בסיסיות.
מדרגה 2:
נתונים ביטויים של חמש פונקציות שהגרף שלהן מוכר לתלמידים.
מדרגה 3:
נתונים ארבעה ביטויים של פונקציות מכפלה ומנה, ועל התלמיד להתאים לכל ביטוי את הגרף המתאים מתוך שישה גרפים נתונים.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. רצוי להיעזר ביישומונים המצורפים.
שימוש ביישומונים:
בכל בעיה ובכל שלב, השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה והגיע למסקנות הנידרשות. אם תלמיד טעה / או לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
שיעורי בית:
סיום המשימה.
הערה:
משימה זו ניתן לשלב בכל שלב של ההוראה, לאחר הפעלת המשימה "הקשר בין גרף הפונקציה \(f{(x)}\) לבין גרף הפונקציה ההופכית \(\frac {1}{f{(x)}}\) חלק א'", כשיעורי בית, הפעלה בכתה, או כהכנה לקראת בחינה. ובכל מקרה רצוי לקיים דיון כיתתי על השאלות שמופיעות במשימה. למשימה קיימת פעילות נוספת: חלק ב'.
משימות מומלצות:
- משימת קדם – פונקציה הופכית – חלק א'
- משימת קדם – פונקציה הופכית – חלק ב'
בעיית מטרה
לפניכם שתי טבלאות:
בטבלה העליונה רשומים מאפיינים של הפונקציה ההופכית \(\Large\frac {1}{f_{n}{(x)}}\).
בטבלה התחתונה רשומים ביטויים של חמש פונקציות \(f_{n}{(x)}\).
- התאימו בין המאפיינים של הפונקציה ההופכית לבין הביטויים של הפונקציות.
שימו לב: למאפיין של פונקציה הופכית יכולים להתאים כמה ביטויים של פונקציות, וכן יכולים להיות ביטויים של פונקציות שאין להם התאמה מבין המאפיינים הנתונים.
\(\space\) - לכל מאפיין של \(\Large\frac {1}{f_{n}{(x)}}\) בטבלה העליונה מצאו עוד ביטוי משלכם המתאים לפונקציה \(\Large\frac {1}{f_{n}{(x)}}\).
לאחר שסיימתם, בדקו תשובותיכם בעזרת היישומון המצורף – בחלק של כתיבה חופשית.
מאפיינים של הפונקציה ההופכית
א. לפונקציה ההופכית אין אסימפטוטות אנכיות.
ב. לפונקציה ההופכית יש יותר מאסימפטוטה אנכית אחת.
ג. מספר נקודות הקיצון של הפונקציה \(f_{n}{(x)}\) שווה למספר נקודות הקיצון של הפונקציה ההופכית שלה \(\Large\frac {1}{f_{n}{(x)}}\).
ד. הפונקציה ההופכית חיובית בכל תחום הגדרתה.
ה. לפונקציה ההופכית אין נקודות קיצון.
ו. הפונקציה \(f_{n}{(x)}\) והפונקציה ההופכית שלה \(\Large\frac {1}{f_{n}{(x)}}\) לא נחתכות ביניהן.
ביטויים עבור הפונקציה \(f_{n}{(x)}\)
\(f_{1}(x)=x^3(x^2-4)\)
\(f_{2}(x)=(x-2)^2(x^2-1)\)
\(f_{3}(x)=x^3(x^2+4)\)
\(f_{4}(x)=\Large\frac{16-x^4}{x^2-4}\)
\(f_{5}(x)=x^4+3x^2+2\)
- במידת הצורך, פתרו את הבעיות במדרגה 1.
- כיתבו בתא המיועד ביטוי אלגברי לפונקציה המבוקשת
מדרגה 1
לפניכם שתי טבלאות:
בטבלה העליונה רשומים מאפיינים של הפונקציה ההופכית \(\Large\frac {1}{t_{n}{(x)}}\).
בטבלה התחתונה רשומים ביטויים של פונקציות \(t_{n}{(x)}\).
התאימו בין המאפיינים של הפונקציה ההופכית לבין הביטויים של הפונקציות.
שימו לב: למאפיין של פונקציה הופכית יכולים להתאים כמה ביטויים של פונקציות, יכולים להיות ביטויים של פונקציות שאין להם התאמה מבין המאפיינים הנתונים ויכול להיות מאפיין שאין פונקציה שמתאימה לו.
תוכלו להיעזר ביישומון המצורף.
מאפיינים של הפונקציה ההופכית
א. לפונקציה ההופכית אין אסימפטוטות אנכיות.
ב. לפונקציה ההופכית יש יותר מאסימפטוטה אנכית אחת.
ג. מספר נקודות הקיצון של הפונקציה \(t_{n}{(x)}\) שווה למספר נקודות הקיצון של הפונקציה ההופכית שלה \(\Large\frac {1}{t_{n}{(x)}}\).
ד. הפונקציה ההופכית חיובית בכל תחום הגדרתה.
ה. לפונקציה ההופכית אין נקודות קיצון.
ו. הפונקציה \(t_{n}{(x)}\) והפונקציה ההופכית שלה \(\Large\frac {1}{t_{n}{(x)}}\) לא נחתכות ביניהן.
ביטויים עבור הפונקציה \(t_{n}{(x)}\)
\(t_{1}(x)=\Large\frac{(x+1)^3}{4x+4}\)
\(t_{2}(x)=(x-2)^6\)
\(t_{3}(x)=x^4-3x^2+2\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
מדרגה 2
לפניכם שתי טבלאות:
בטבלה העליונה רשומים מאפיינים של הפונקציה ההופכית \(\Large\frac {1}{g_{n}{(x)}}\).
בטבלה התחתונה רשומים ביטויים של פונקציות \(g_{n}{(x)}\).
התאימו בין המאפיינים של הפונקציה ההופכית לבין הביטויים של הפונקציות.
שימו לב: למאפיין של פונקציה הופכית יכולים להתאים כמה ביטויים של פונקציות, יכולים להיות ביטויים של פונקציות שאין להם התאמה מבין המאפיינים הנתונים ויכול להיות מאפיין שאין פונקציה שמתאימה לו.
תוכלו להיעזר ביישומון המצורף.
מאפיינים של הפונקציה ההופכית
א. לפונקציה ההופכית אין אסימפטוטות אנכיות.
ב. לפונקציה ההופכית יש יותר מאסימפטוטה אנכית אחת.
ג. מספר נקודות הקיצון של הפונקציה \(g_{n}{(x)}\) שווה למספר נקודות הקיצון של הפונקציה ההופכית שלה \(\Large\frac {1}{g_{n}{(x)}}\).
ד. הפונקציה ההופכית חיובית בכל תחום הגדרתה.
ה. לפונקציה ההופכית אין נקודות קיצון.
ו. הפונקציה \(g_{n}{(x)}\) והפונקציה ההופכית שלה \(\Large\frac {1}{g_{n}{(x)}}\) לא נחתכות ביניהן.
ביטויים עבור הפונקציה \(g_{n}{(x)}\)
\(g_{2}(x)=-(x+5)^2\)
\(g_{3}(x)=(x-2)(x+5)\)
\(g_{4}(x)=(x-2)^3\)
\(g_{5}(x)=\Large\frac{(x-2)^2}{2x-4}\)
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
ביטויים עבור הפונקציה \(h_{n}{(x)}\)
\(h_{2}(x)=\Large\frac{(x+2)(3x-3)}{x-1}\)
\(h_{3}(x)=(x^2+1)(x^2+4)\)
\(h_{4}(x)=-x^3(x^2+1)\)
גרפים של הפונקציות \(h_{n}{(x)}\)
I
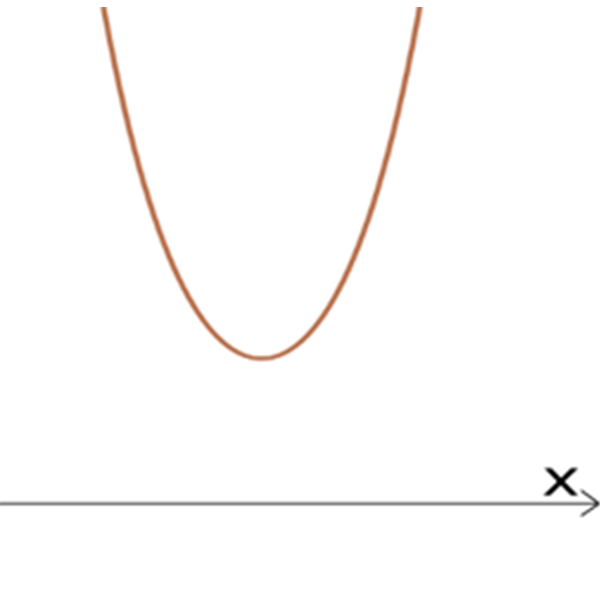
II
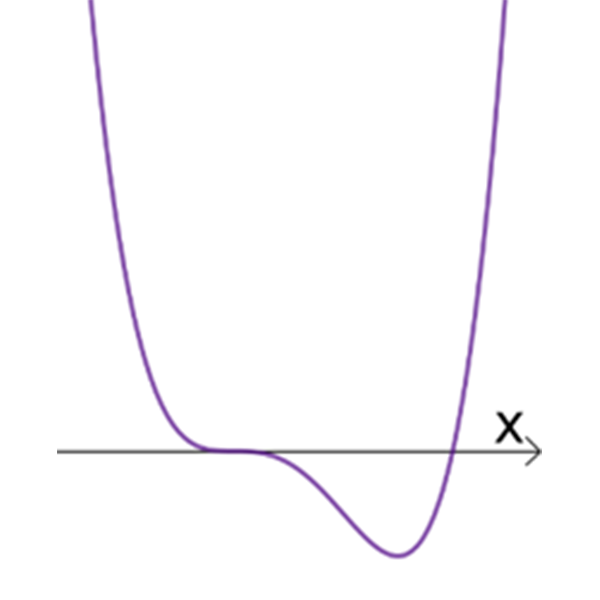
III
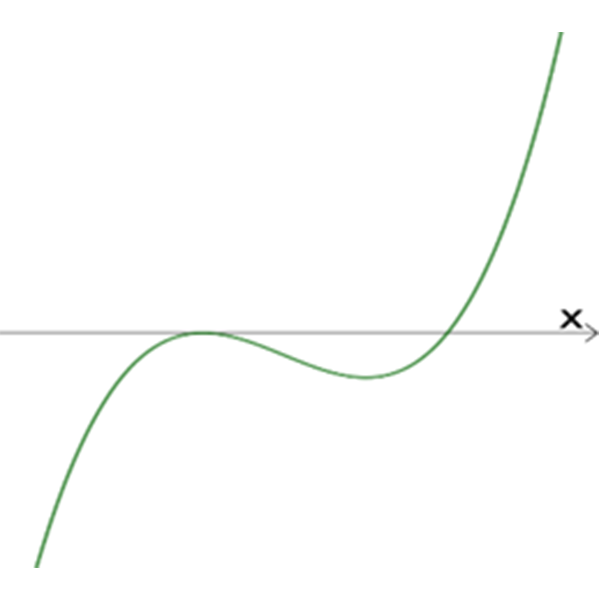
IV
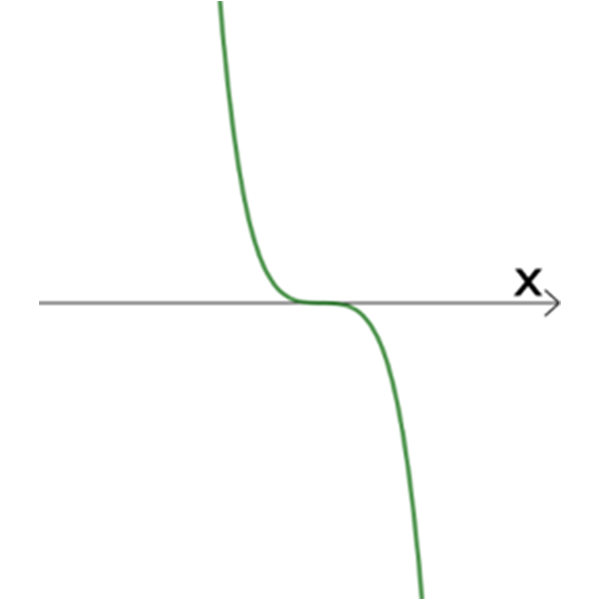
V
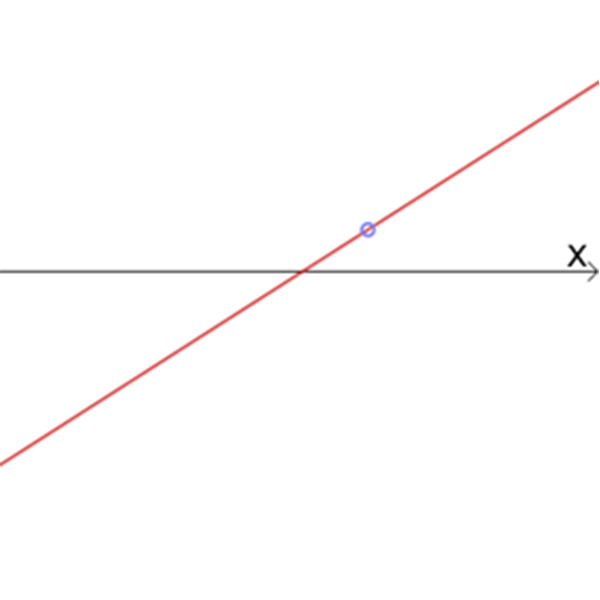
VI
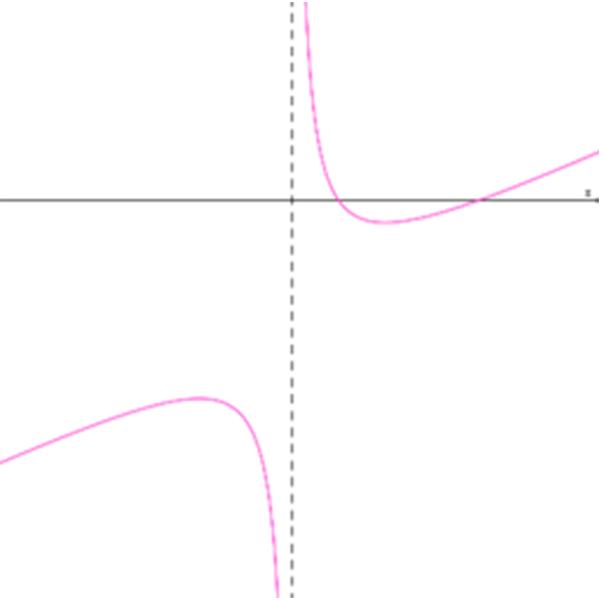
- לפניכם, בטבלה למטה, רשומים מאפיינים של הפונקציה ההופכית \(\Large\frac {1}{h_{n}{(x)}}\).
התאימו בין המאפיינים של הפונקציה ההופכית לבין הביטויים של הפונקציות \(h_{n}{(x)}\).
שימו לב: למאפיין של פונקציה הופכית יכולים להתאים כמה ביטויים של פונקציות, וכן יכולים להיות ביטויים של פונקציות שאין להם התאמה מבין המאפיינים הנתונים.
מאפיינים של הפונקציה ההופכית
א. לפונקציה ההופכית אין אסימפטוטות אנכיות.
ב. לפונקציה ההופכית יש יותר מאסימפטוטה אנכית אחת.
ג. מספר נקודות הקיצון של הפונקציה \(h_{n}{(x)}\) שווה למספר נקודות הקיצון של הפונקציה ההופכית שלה \(\Large\frac {1}{h_{n}{(x)}}\).
ד. הפונקציה ההופכית חיובית בכל תחום הגדרתה.
ה. לפונקציה ההופכית אין נקודות קיצון.
ו. ייתכן שהפונקציה \(h_{n}{(x)}\) והפונקציה ההופכית שלה \(\Large\frac {1}{h_{n}{(x)}}\) לא נחתכות ביניהן.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















