קשרים בין הפונקציה \(f(x)\) לבין פונקציית השורש הריבועי \(\sqrt{f(x)}\) - חלק א' - למורה
חומר לימוד:
סרטוט הגרף של הפונקציה \(\sqrt{f(x)}\) כאשר נתון הגרף של הפונקציה \(f(x)\), עבור \(f(x)\) פולינום.
כיתה:
כיתה י' / כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש בעיות מדרגה. לכל מדרגה מותאמים יישומונים.
ידע קודם:
- הכרת פונקציות פולינום מסוגים שונים.
- הכרת פונקציית השורש \(\sqrt{x}\).
- תכונות של פונקציה: תחום הגדרה, נקודות חיתוך עם הצירים, נקודות קיצון וסוגן, תחומי עליה וירידה, תחומי חיוביות ושליליות, נקודות חיתוך בין פונקציות, מצב הדדי בין פונקציות.
המשימה מתאימה להפעלה בהתחלה של הוראת הנושא, לאחר שתלמידים הכירו את פונקציית השורש הריבועי \(\sqrt{x}\).
מטרות לימודיות:
- זיהוי והבנה של קשרים בין תכונות פונקציית פולינום \(f(x)\) לבין תכונות הפונקציה \(\sqrt{f(x)}\) בלי להיעזר בנגזרת של פונקציית השורש. בשלב למידה מאוחר יותר ניתן לקשר בין משימה זו לנגזרת של פונקציית השורש הריבועי.
- נקודות חיתוך בין \(f(x)\) ל-\(\sqrt{f(x)}\).
- המצב ההדדי בין הגרפים של הפונקציות \(f(x)\) ו-\(\sqrt{f(x)}\).
- פונקציית שורש של פרבולה שקודקודה על ציר ה- \(x\).
משימת המטרה:
נתונים שני גרפים של שתי פונקציות מורכבות. יש לסרטט את הגרפים של \(\sqrt{f(x)}\), ולמצוא את הקשרים בין \(f(x)\) ל-\(\sqrt{f(x)}\).
מדרגה 1:
נתונות שתי בעיות דומות לבעיית המטרה עבור פונקציות פשוטות: גרפים של פרבולה משיקה לציר \(x\) ופולינום ממעלה שלישית עם 3 נקודות אפס ושאלות המכונות למציאת הקשרים בין \(f(x)\) ל-\(\sqrt{f(x)}\).
מדרגה 2:
נתונות שתי בעיות, פרבולה בעלת מינימום ושתי נקודות חיתוך עם ציר \(x\) ופולינום ממעלה שלישית שמתאפס פעם אחת ושאלות ממוקדות למציאת הקשרים בין \(f(x)\) ל-\(\sqrt{f(x)}\).
מדרגה 3:
ארבע בעיות: גרפים של שתי פרבולות, גרף לינארי וגרף דומה לפרבולה ושאלות ממוקדות.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. רצוי להיעזר ביישומונים המצורפים.
שימוש ביישומונים:
בכל בעיה ובכל שלב, השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה והגיע למסקנות הנידרשות. אם תלמיד טעה / או לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
שיעורי בית:
סיום המשימה.
משימות מומלצות:
משימת המשך והעמקה למשימה זו – קשרים בין פונקציה לבין פונקציית השורש הריבועי – חלק ב.
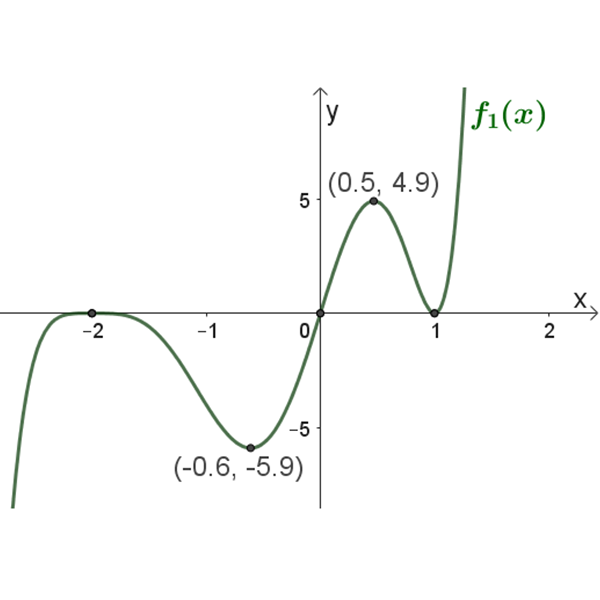
\(f_1{(x)}\)
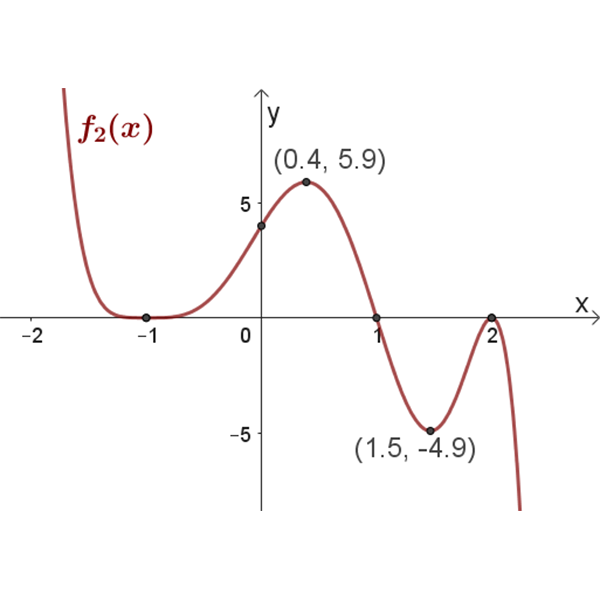
\(f_2{(x)}\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-2,0)\)
נקודות קיצון: מקסימום \((0.5,4.9)\) , \((-2,0)\) מינימום \((0.5,4.9)\) , \((-0.6,-5.9)\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((0,4)\) , \((2,0)\) , \((1,0)\) , \((-1,0)\)
נקודות קיצון: מקסימום \((2,0)\) , \((0.4,5.9)\) מינימום \((1.5,-4.9)\) , \((-1,0)\)
- לכל אחד מהגרפים של \(f_n{(x)}\), סרטטו באותה מערכת צירים, את גרף הפונקציה \(\sqrt{f_n{(x)}}\)
שימו לב גם למצב ההדדי בין הפונקציות.
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- פתרתם, מצאו וסכמו מהם הקשרים בין פונקציית פולינום כלשהי \(f(x)\) לבין \(\sqrt{f(x)}\).
תוכלו להיעזר ביישומונים הדינאמיים המצורפים לבדיקת תשובתכם.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- כדי לעבור לפונקציה האחרת יש ללחוץ על שנה פונקציה, בכפתור הצהוב בתפריט שבתחתית היישומון.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים).
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הורודה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.
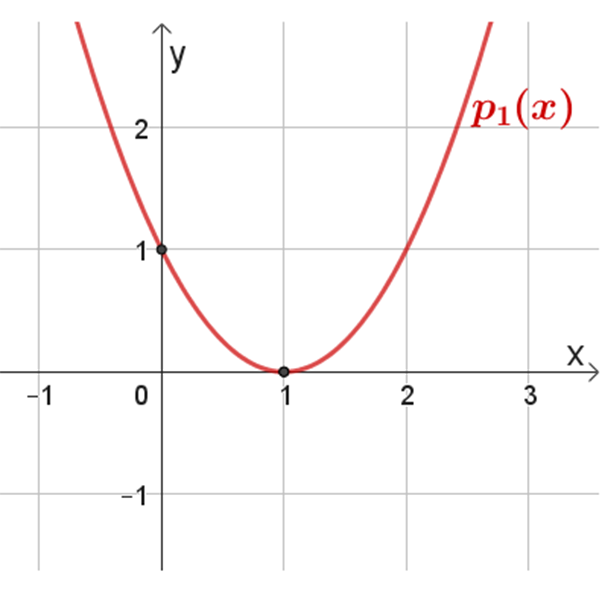
\(p_1{(x)}\)
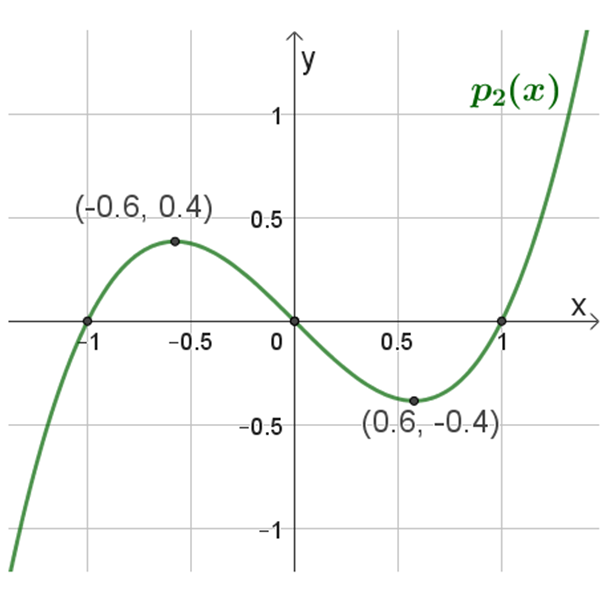
\(p_2{(x)}\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,1)\)
נקודת מינימום: \((1,0)\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-1,0)\)
נקודות קיצון: מקסימום: \((-0.6,0.4)\) , מינימום: \((0.6,-0.4)\)
סעיף א
לכל אחד מהגרפים של \(p_n{(x)}\), סרטטו באותה מערכת צירים, את גרף הפונקציה \(\sqrt{p_n{(x)}}\).
שימו לב גם למצב ההדדי בין הפונקציות \(p_n{(x)}\) ו- \(\sqrt{p_n{(x)}}\)
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
סעיף ב
נתונה פונקציה \(f{(x)}\) כלשהי.
ענו על השאלות הבאות, בכל סעיף נמקו תשובתכם:
- מה הקשר ביו תחום ההגדרה של \(\sqrt{f(x)}\) לתכונות הפונקציה \(f(x)\)?
- מה הקשר בין נקודות הקיצון וסוגן של \(\sqrt{f(x)}\) לתכונות הפונקציה \(f(x)\)?
- באילו מקרים הפונקציות \(f(x)\) ו- \(\sqrt{f(x)}\) נחתכות, ומה ניתן להסיק ביחס לשיעורי נקודות החיתוך בין הפונקציות?
- באילו מקרים גרף הפונקציה \(\sqrt{f(x)}\) יהיה כולו מתחת לגרף פונקציה \(f(x)\)?
- נתון כי בתחום \(a<x<b\) מתקיים: \(0<f(x)<1\). מה המצב ההדדי בין \(f(x)\) ל- \(\sqrt{f(x)}\) בתחום זה?
- האם הפונקציה \(h(x)=\sqrt{x^2}\) מתלכדת עם הפונקציה \(k(x)=x\)?
תוכלו להיעזר ביישומונים הדינאמיים המצורפים לבדיקת תשובותיכם.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- כדי לעבור לפונקציה האחרת יש ללחוץ על שנה פונקציה, בכפתור הצהוב בתפריט שבתחתית היישומון.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים).
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הורודה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.
\(h_1{(x)}\)
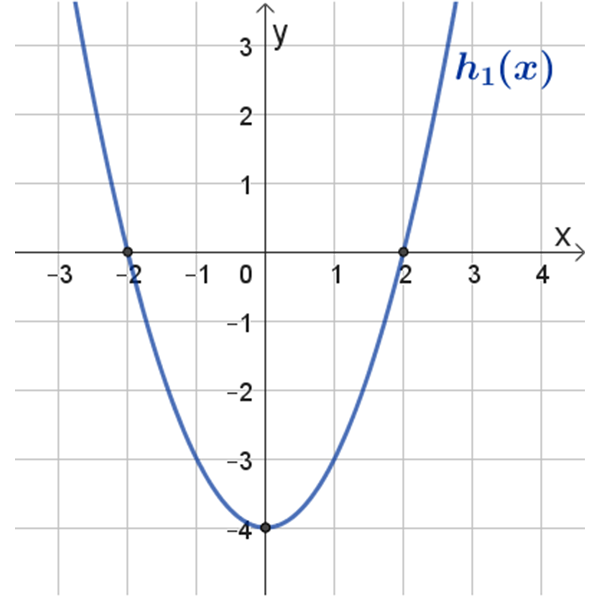
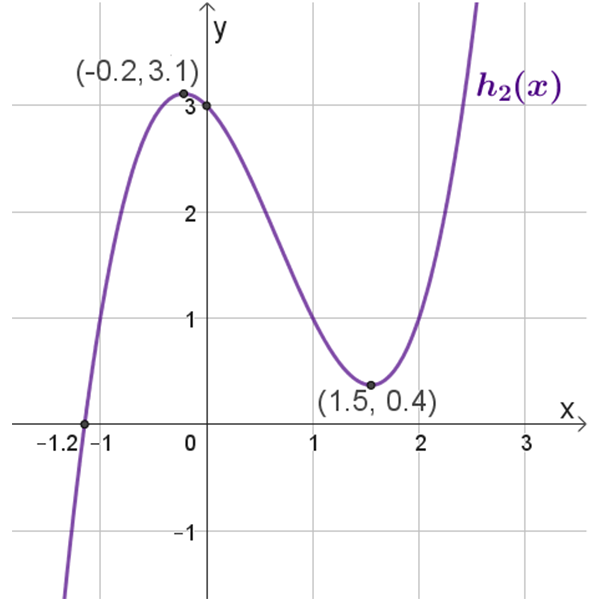
\(h_2{(x)}\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((0,-4)\) , \((2,0)\) , \((-2,0)\)
נקודת מינימום: \((0,-4)\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((0,3)\) , \((-1.2,0)\)
נקודות קיצון: מקסימום \((-0.2,3.1)\) מינימום \((1.5,0.4)\)
סעיף א
לכל אחד מהגרפים של \(h_n{(x)}\), סרטטו באותה מערכת צירים, את גרף הפונקציה \(\sqrt{h_n{(x)}}\).
שימו לב גם למצב ההדדי בין הפונקציות \(h_n{(x)}\) ו- \(\sqrt{h_n{(x)}}\)
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
סעיף ב
נתונה פונקציה \(f{(x)}\) כלשהי.
ענו על השאלות הבאות, בכל סעיף נמקו תשובתכם:
- באילו מקרים יש לפונקציה \(\sqrt{f(x)}\) נקודות קצה?
מה ניתן לומר עליהן? - מה צריכים להיות שיעורי \(f(x)\) כדי שלמשוואה \(f(x)=\sqrt{f(x)}\) יהיו פתרונות?
שימו לב למקרים שונים והתייחסו לכל האפשרויות. - מהו סדר הגודל (מי קטן, מי גדול) בין מספר חיובי קטן מ-1 לשורש של אותו מספר?
- מהו סדר הגודל בין מספר גדול מ-1 לבין השורש של אותו מספר?
תוכלו להיעזר ביישומונים הדינאמיים המצורפים לבדיקת תשובותיכם.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- כדי לעבור לפונקציה האחרת יש ללחוץ על שנה פונקציה, בכפתור הצהוב בתפריט שבתחתית היישומון.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים).
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הורודה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.
\(g_1{(x)}\)
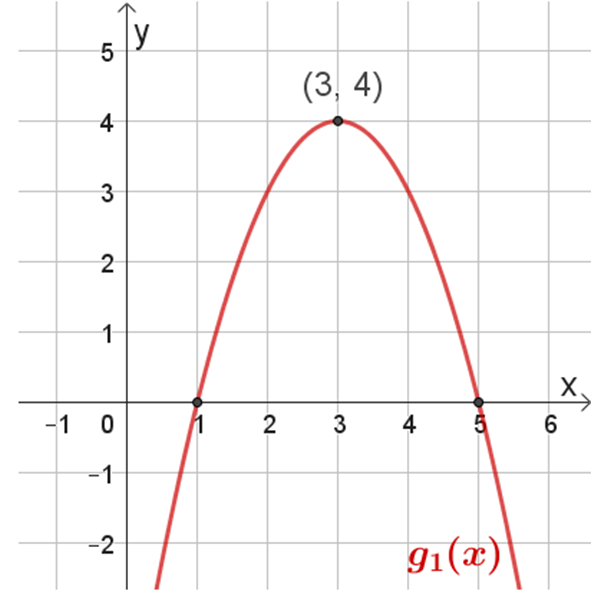
\(g_2{(x)}\)
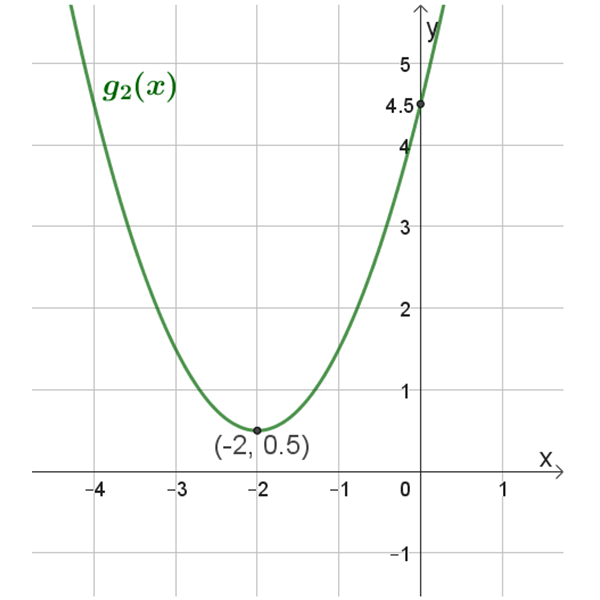
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((0,-5)\) , \((5,0)\) , \((1,0)\)
נקודת מקסימום: \((3,4)\)
תחום הגדרה: כל \(x\)
נקודת חיתוך עם ציר \(y\): \((0,4.5)\)
נקודת מינימום: \((-2,0.5)\)
\(g_3{(x)}\)
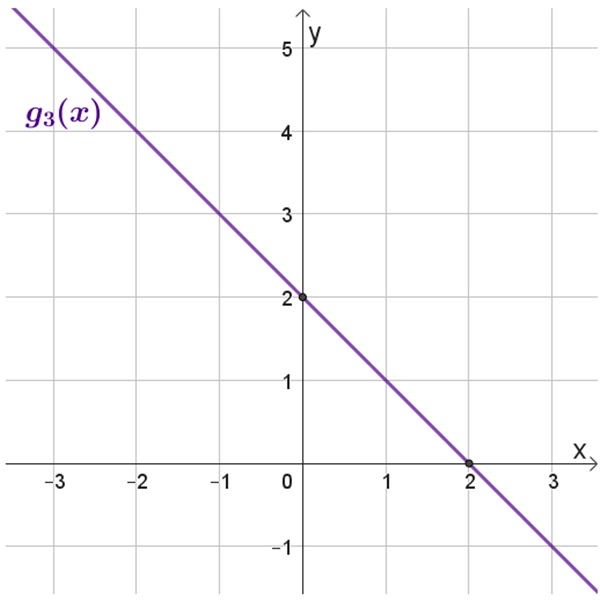
\(g_4{(x)}\)
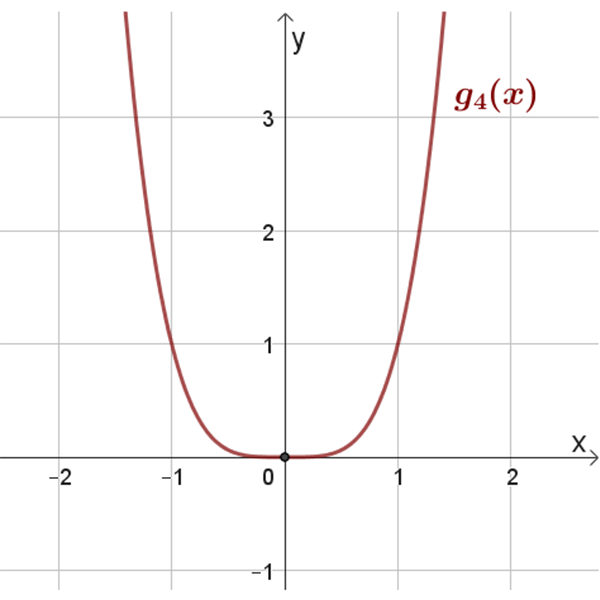
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((2,0)\) , \((0,2)\)
תחום הגדרה: כל \(x\)
נקודת חיתוך עם הצירים: \((0,0)\)
נקודת מינימום \((0,0)\)
סעיף א
לכל אחד מהגרפים של \(g_n{(x)}\), סרטטו באותה מערכת צירים, את גרף הפונקציה \(\sqrt{g_n{(x)}}\).
שימו לב גם למצב ההדדי בין הפונקציות \(g_n{(x)}\) ו- \(\sqrt{g_n{(x)}}\)
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
סעיף ב
נתונה פונקציה \(f{(x)}\) כלשהי.
ענו על השאלות הבאות, בכל סעיף נמקו תשובתכם:
- אם \(0<f(x_1)<f(x_2)\), אז
מהו סדר הגודל בין \(\sqrt{f({x_1})}\) לבין \(\sqrt{f({x_2})}\)?
מה ניתן להסיק מכך? - אם \(f(x)=4\) אז \(\sqrt{f(x)}=?\)
אם \(f(x)=0\) אז \(\sqrt{f(x)}=?\)
אם \(f(x)=1\) אז \(\sqrt{f(x)}=?\)
אם \(f(x)=-1\) אז \(\sqrt{f(x)}=?\)
לכן, אילו נקודות יכולות להיות נקודות חיתוך בין \(f(x)\) לבין \(\sqrt{f(x)}\)? - אם \(f(x)>1\) אז האם
\(\sqrt{f(x)}>f(x)\) או \(\sqrt{f(x)}<f(x)\)?
נמקו תשובתכם. (תוכלו להיעזר בדוגמה מספרית)אם \(0<f(x)<1\) אז האם
\(\sqrt{f(x)}>f(x)\) או \(\sqrt{f(x)}<f(x)\)?
נמקו תשובתכם. (תוכלו להיעזר בדוגמה מספרית)
תוכלו להיעזר ביישומונים הדינאמיים המצורפים לבדיקת תשובותיכם.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- כדי לעבור לפונקציה האחרת יש ללחוץ על שנה פונקציה, בכפתור הצהוב בתפריט שבתחתית היישומון.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים).
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הורודה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.