הוכחות באמצעות שטחים – מפגש תיכונים - למורה

משימה לתלמיד

דף למורה

מבנה המשימה

יישומונים

  • – – – – –
חומר לימוד:

הוכחת המשפט בדבר נקודת מפגש התיכונים במשולש באמצעות השוואת שטחי משולשים.

כיתה:

כיתה י'

מבנה המשימה:

המשימה מנחה להוכיח את המשפט באמצעות שיקולים של השוואת שטחים, שיטה יעילה ונדרשת בפתרון בעיות הוכחה ותרגילי חישוב בגיאומטריה.

משימה זו היא אחת משלוש משימות שמכוונות לשימוש בשיטה זו – המשפט בדבר נקודת מפגש התיכונים, משפט תאלס, המשפט ההפוך לו ותכונת חוצה הזווית במשולש.

מבנה:

בעיית מטרה ושלוש מדרגות.

ידע קודם:

חישוב שטח משולש באמצעות מחצית מכפלת האורכים של צלע בגובה לצלע.

מטרות לימודיות:
  • הוכחת משפט מרכזי בתכנית הלימודים.
  • תרגול השימוש בשיקולים של חישובי שטחים – שיקולים שנדרשים בשאלות אחרות.
משימת המטרה:

הוכחת המשפט על מפגש תיכונים במשולש באמצעות שטחים

מדרגה 1:

יש למצוא משולשים שווי שטח במשולש בו הועברו תיכונים.

מדרגה 2:

מציאת יחס בין שטחי משולשים בטרפז וכתוצאה מכך – יחס קטעים.

מדרגה 3:

משולש מחולק לשני משולשים, בו יש למצוא את יחס השטחים.

שיטת הוראה: בכיתה:

עבודה עצמאית או בזוגות. התלמידים יתחילו בבעיית המטרה ויעברו למדרגות השונות באופן עצמאי או בהנחיית המורה.

כל התלמידים יתמודדו עם הוכחת המשפט המופיע בתכנית הלימודים.

משימות מומלצות: משימות נוספות הקשורות להוכחות באמצעות שטחים:

בעיית מטרה

הוכיחו את המשפט בדבר מפגש התיכונים במשולש:
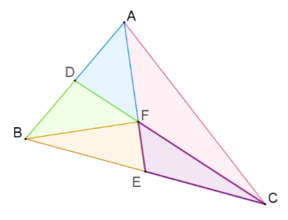
  1. נקודת המפגש של כל שני תיכונים מחלקת כל אחד מהם ביחס 1:2, כך שהחלק הארוך קרוב לקודקוד.
  2. בכל משולש שלושת התיכונים נפגשים בנקודה אחת.
  • במידת הצורך פתרו את הבעיות במדרגה 1.

מדרגה 1

  1. נתון: \(AE\) ו- \(CD\) תיכונים במשולש \(\triangle ABC\) הנפגשים בנקודה \(F\).
    מה ניתן לומר על שטחי המשולשים: \(\triangle ABE\) ו- \(\triangle ACE\)?

   2. רשמו את כל המשולשים בסרטוט השווים בשטחם.

  • אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
  • או, במידת הצורך, פתרו את הבעיות במדרגה 2.

מדרגה 2

בטרפז \(ABCD\) אלכסוני הטרפז נחתכים בנקודה \(E\).
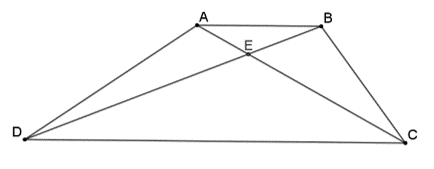
  1. הוכיחו:  \(S_{\triangle BEC}=S_{\triangle AED} \)
    \(\space\)
  2. נתון כי: \(S_{\triangle ABC}=ר"מס\space4\) , \(S_{\triangle BCD}=ר"מס\space12\)
    מצאו את היחס: \(\Large\frac{AB}{CD}\)
  • אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
  • או, במידת הצורך, פתרו את הבעיות במדרגה 3.

מדרגה 3

סעיף א

בסרטוט נתון משולש  \(S_{\triangle ABC}\).

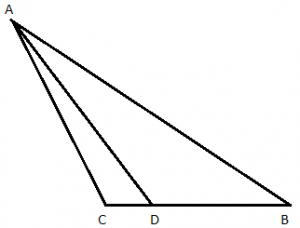
הנקודה \(D\) נמצאת על הקטע \(BC\) כך ש \(BD=3CD\).
מצאו את היחס \(\Large\frac{S_{\triangle ADC}}{S_{\triangle ABD}}\)

סעיף ב

בסרטוט נתון \(AE\)  ו- \(CD\) תיכונים.

סמנו: \(S_{\triangle BDF}=S_1\) , \(S_{\triangle BFE}=S_2\)
ובטאו את   \(S_{\triangle AEC}\) באמצעות \(S_1\) ובאמצעות \(S_2\).