שטחים, תאלס ועוד במשולש וטרפז - למורה
חומר לימוד:
פתרון בעיות הוכחה בגיאומטריה
כיתה:
כיתה י' / כיתה י"א
מבנה המשימה:
בעיית מטרה אחת ושלוש מדרגות
ידע קודם:
- משפט תאלס
- דמיון משולשים
- מציאת שטח משולשים
מטרות לימודיות:
- פיתוח חשיבה אסטרטגית
- יכולת לחלק בעיה לתת-בעיות
- תרגול בנושאים: דמיון משולשים, משפט תאלס, תיכון מחלק משולש לשני משולשים שווי שטח
משימת המטרה:
הוכחת שוויון שטחים בין משולשים. לצורך ההוכחה נדרש שימוש בדמיון משולשים, או משפט תאלס.
מדרגה 1:
שימוש במשפט תאלס ודמיון.
מדרגה 2:
הוכחת התכונה: נקודת המפגש של האלכסונים חוצה את המקביל לבסיסים העובר דרכה. לצורך הוכחה נדרש שימוש במשפט תאלס.
מדרגה 3:
שימוש במשפט תאלס במשולש.
שיטת הוראה:
בכיתה:
עבודה בזוגות. התלמידים מתקדמים ממשימה למדרגה ובין המדרגות בהתאם לרצונם או בהדרכת המורה.
לאחר פתרון הבעיות מומלץ לקיים דיון כיתתי.
שימוש ביישומונים:
אין
שיעורי בית:
סיום המשימה.
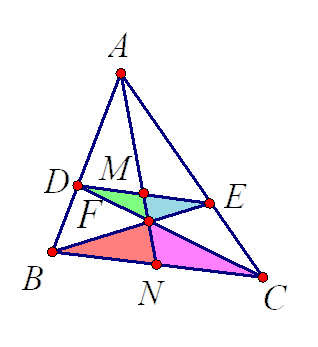
הוכיחו:
\(S_{\triangle{DMF}}=S_{\triangle{EMF}}\) וגם \(S_{\triangle{BFN}}=S_{\triangle{CFN}}\)
- במידת הצורך פתרו את הבעיות במדרגה 1.
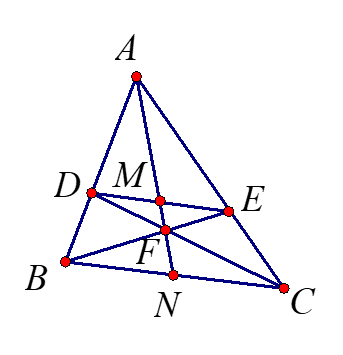
מצאו את כל המשולשים הדומים.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
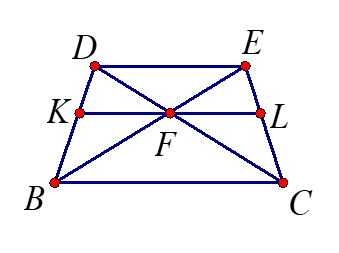
הוכיחו: \(FL=KF\)
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.

הוכיחו:
- \(\Large\frac{DM}{BN}\normalsize=\Large\frac{EM}{CN}\)
\(\space\) - \(\Large\frac{DM}{CN}\normalsize=\Large\frac{EM}{BN}\)
\(\space\) - הקטע \(AN\) הוא תיכון במשולש \(ABC\).
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















