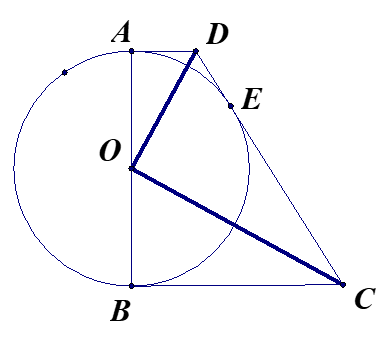
שני משולשים במרובע ומעגל - למורה
חומר לימוד:
פתרון בעיות הוכחה בגיאומטריה
כיתה:
כיתה י' / כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות. לכל שלב מצורף יישומון.
ידע קודם:
- תכונות מעגל
- משיקים למעגל
- תכונות טרפז
- שטח משולש
מטרות לימודיות:
- פיתוח חשיבה אסטרטגית
- יכולת לחלק בעיה לתת-בעיות
סוג הדירוג:
פתרון הבעיות במדרגות תומך בפתרון בעיית המטרה
משימת המטרה:
בעיה כללית. טרפז מעגל ושני משולשים. יש להוכיח את יחס שטחי המשולשים.
מדרגה 1:
טרפז, מעגל ומרובע. יש להוכיח מהו סוג המרובע.
מדרגה 2:
טרפז ומעגל. יש להוכיח שמתקבלת זווית ישרה.
מדרגה 3:
טרפז מעגל ומרובע. יש להוכיח שהמרובע הוא מלבן.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה.
אחרי פתרון הבעיות מומלץ לקיים דיון כיתתי.
שימוש ביישומונים:
לכל שלב יש יישומון מתאים.
שיעורי בית:
סיום המשימה.
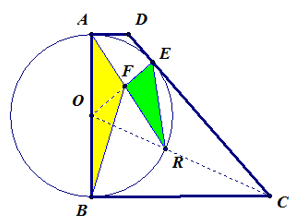
הוכיחו: שטח משולש \(\triangle AFB\) גדול פי 2 משטח משולש \(\triangle EFR\).
היעזרו ביישומון.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- גרירת נקודות \(A\) או \(E\), מציגה מרובע ומשולשים שונים, תוך שמירה על הנתונים.
- כדי ל"נקות" את היישומון ולהתחיל מחדש ניתן להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
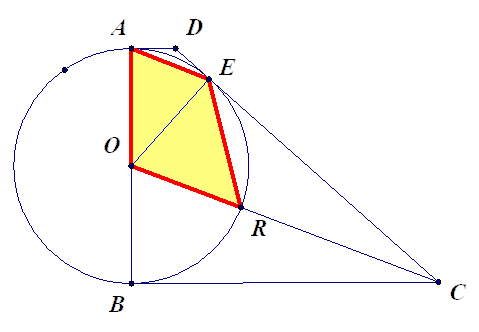
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- גרירת נקודות \(A\) או \(E\), מציגה מרובע ומשולשים שונים, תוך שמירה על הנתונים.
- כדי ל"נקות" את היישומון ולהתחיל מחדש ניתן להיעזר בחיצי האתחול שבפינה הימנית העליונה.
- גרירת נקודות \(A\) או \(E\), מציגה מרובע ומשולשים שונים, תוך שמירה על הנתונים.
- כדי ל"נקות" את היישומון ולהתחיל מחדש ניתן להיעזר בחיצי האתחול שבפינה הימנית העליונה.
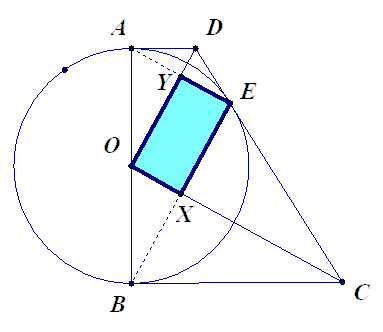
הוכיחו: \(OYEX\) מלבן (מצאו לפחות 3 דרכים שונות).
היעזרו ביישומון.
- נתון: גם: \(R\) – נקודת חיתוך של \(OC\) עם המעגל.
המרובע \(AERO\) הוא טרפז \((AE∥OR)\).
\(F\) – נקודת חיתוך \(OE\) ו- \(AR\).
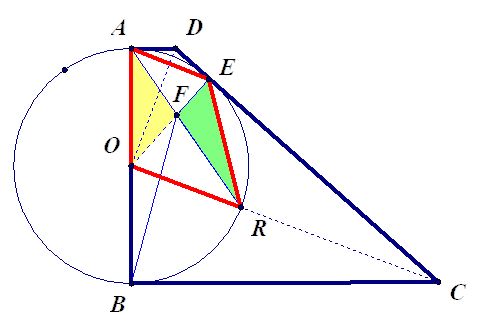
הוכיחו: שטח משולש \(\triangle{AFO}\) שווה לשטח משולש \(\triangle{EFR}\).
תוכלו להיעזר ביישומון.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- גרירת נקודות \(A\) או \(E\), מציגה מרובע ומשולשים שונים, תוך שמירה על הנתונים.
- כדי ל"נקות" את היישומון ולהתחיל מחדש ניתן להיעזר בחיצי האתחול שבפינה הימנית העליונה.
- גרירת נקודות \(A\) או \(E\), מציגה מרובע ומשולשים שונים, תוך שמירה על הנתונים.
- כדי ל"נקות" את היישומון ולהתחיל מחדש ניתן להיעזר בחיצי האתחול שבפינה הימנית העליונה.