קשרים בין הפונקציה \(f(x)\) לבין פונקציית השורש הריבועי \(\sqrt{f(x)}\) - חלק ב' - למורה
חומר לימוד:
העמקת הידע של הקשרים בין תכונות של פונקציית פולינום \(f(x)\) לפונקציות \(\sqrt{f(x)}\) ו- \(f^2(x)\). שילוב בין פעולת השורש הריבועי של פונקציה לבין הזזות.
כיתה:
כיתה י' / כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות. מצורפים יישומונים לבעיית המטרה ולמדרגות.
ידע קודם:
הכרת:
- הפונקציה הריבועית ותכונותיה.
- פונקציות פולינום מסוגים שונים.
- פונקציית השורש \(\sqrt(x)\), והכרת הקשרים בין הפונקציה \(f(x)\) לבין פונקציית השורש הריבועי \(\sqrt{f(x)}\).
- ריבוע של פונקציה \(f(x)\).
- תכונות של פונקציה: תחום הגדרה, נקודות חיתוך עם הצירים, נקודות קיצון וסוגן, תחומי עליה וירידה, תחומי חיוביות ושליליות.
- נקודות חיתוך בין פונקציות, מצב הדדי בין פונקציות.
מטרות לימודיות:
- זיהוי והבנה של קשרים בין תכונות פונקציית פולינום \(f(x)\) לבין הפונקציה \(\sqrt{f(x)}\).
- נקודות חיתוך בין \(f(x)\) ל- \(\sqrt{f(x)}\) והמצב ההדדי בין הגרפים של הפונקציות.
- זיהוי והבנה של קשרים בין \(f(x)\) לבין הפונקציה \(\sqrt{f(x)}\), לבין \(f^2(x)\) בשילוב הזזות.
המשימה מתאימה להפעלה לאחר שתלמידים הכירו את קשרים בין הפונקציה \(f(x)\) לבין פונקציית השורש הריבועי \(\sqrt{f(x)}\) (ראו חלק א' של המשימה) ולאחר הפעלת המשימה "חזקה שניה של פונקציה".
משימת המטרה:
נתון פולינום החותך את ציר ה-\(x\) בארבע נקודות.
מדרגה 1:
נתון פולינום החותך את ציר ה-\(x\) בשלוש נקודות.
מדרגה 2:
נתונה פונקציה קעורה כלפי מטה ולה שתי נקודות חיתוך עם ציר ה-\(x\).
מדרגה 3:
נתונה פונקציה קעורה כלפי מעלה שאין לה חיתוך עם ציר \(x\).
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. רצוי להיעזר ביישומונים המצורפים.
שימוש ביישומונים:
בכל בעיה ובכל שלב, השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה והגיע למסקנות הנידרשות. אם תלמיד טעה / או לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
שיעורי בית:
סיום המשימה.
משימות מומלצות:
משימות קדם למשימה זו:
\(f(x)\)
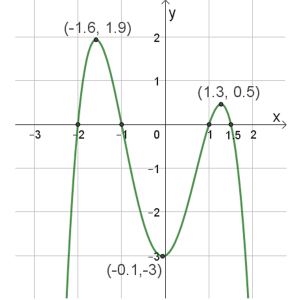
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((0,-3)\) , \((1.5,0)\) , \((1,0)\) , \((-1,0)\) , \((-2,0)\)
נקודות קיצון: מקסימום \((1.3,0.5)\) , \((-1.6,9)\) מינימום \((-0.1,-3)\)
- סרטטו, באותה מערכת צירים, בצבעים שונים, סקיצות של הגרפים של:
א. \(\sqrt{f(x)}\)
ב. \(f^2(x)\) - כמה פתרונות יש למשוואה הבאה: \(f(x+1)=\sqrt{f(x+1)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(f^2(x+1)=\sqrt{f(x+1)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(f(x)-1.5=\sqrt{f(x)-1.5}\)?
נמקו תשובתכם. - באיזה תחום מתקיים: \(\sqrt{f(x+1)}>f^2(x+1)\)? (דייקו ככל האפשר בתשובתכם).
סרטטו ובדקו תשובותיכם לסעיפים השונים בעזרת היישומון המצורף.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות תכלת (לסרטוט \(\sqrt{f(x)}\)) ולפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) במקומות המתאימים להן.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- לצורך התאמת פונקציה אחרת, ניתן לשנות את ערכי הפרמטרים בסרגלי הגרירה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבצד ימין של היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
\(h(x)\)
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-2,0)\)
נקודות קיצון של הפונקציה: מקסימום: \((0.5,0.6)\) , מינימום: \((-1.2,-2.1)\)
- סרטטו, באותה מערכת צירים, בצבעים שונים, סקיצות של הגרפים של:
א. \(\sqrt{h(x)}\)
ב. \(h^2(x)\) - כמה פתרונות יש למשוואה הבאה: \(h(x-2)=\sqrt{h(x-2)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(h^2(x-2)=\sqrt{h(x-2)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(h(x)+1=\sqrt{h(x)+1}\)?
נמקו תשובתכם. - באיזה תחום מתקיים: \(\sqrt{h(x-2)}>h^2(x-2)\)? (דייקו ככל האפשר בתשובתכם).
סרטטו ובדקו תשובותיכם לסעיפים השונים בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות תכלת (לסרטוט \(\sqrt{f(x)}\)) ולפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) במקומות המתאימים להן.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- לצורך התאמת פונקציה אחרת, ניתן לשנות את ערכי הפרמטרים בסרגלי הגרירה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבצד ימין של היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
\(g(x)\)
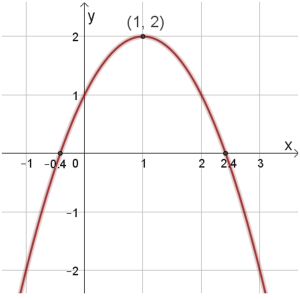
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((0,1)\) , \((2.4,0)\) , \((-0.4,0)\)
נקודת מקסימום: \((1,2)\)
- סרטטו, באותה מערכת צירים, בצבעים שונים, סקיצות של הגרפים של:
א. \(\sqrt{g(x)}\)
ב. \(g^2(x)\) - כמה פתרונות יש למשוואה הבאה: \(g(x+2)=\sqrt{g(x+2)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(g^2(x+2)=\sqrt{g(x+2)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(g(x)-1=\sqrt{g(x)-1}\)?
נמקו תשובתכם. - באיזה תחום מתקיים:
\(g^2(x+2)<\sqrt{g(x+2)}\)?
(דייקו ככל האפשר בתשובתכם).
סרטטו ובדקו תשובותיכם לסעיפים השונים בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות תכלת (לסרטוט \(\sqrt{f(x)}\)) ולפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) במקומות המתאימים להן.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- לצורך התאמת פונקציה אחרת, ניתן לשנות את ערכי הפרמטרים בסרגלי הגרירה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבצד ימין של היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
\(p(x)\)
תחום הגדרה: כל \(x\)
נקודת חיתוך עם הצירים: \((0,0.8)\)
נקודת מינימום: \((0,0.8)\)
- סרטטו, באותה מערכת צירים, בצבעים שונים, סקיצות של הגרפים של:
א. \(\sqrt{p(x)}\)
ב. \(p^2(x)\) - כמה פתרונות יש למשוואה הבאה: \(p(x+1)=\sqrt{p(x+1)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(p^2(x+1)=\sqrt{p(x+1)}\)?
נמקו תשובתכם. - כמה פתרונות יש למשוואה הבאה: \(p(x)-2=\sqrt{p(x)-2}\)?
נמקו תשובתכם. - באיזה תחום מתקיים: \(\sqrt{p(x+1)}>p^2(x+1)\)?
(דייקו ככל האפשר בתשובתכם).
סרטטו ובדקו תשובותיכם לסעיפים השונים בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות תכלת (לסרטוט \(\sqrt{f(x)}\)) ולפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) במקומות המתאימים להן.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- לצורך התאמת פונקציה אחרת, ניתן לשנות את ערכי הפרמטרים בסרגלי הגרירה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבצד ימין של היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.