אינטגרלים: פונקציה ונגזרתה - חלק ב' - למורה
חומר לימוד:
מציאת אינטגרל באמצעות זיהוי פונקציה וכפל בנגזרתה, או מנת נגזרת בפונקציה ובפעולות על פונקציה ללא הביטוי של הפונקציה.
השאלה מתאימה לסיכום וגם לחזרה לקראת בחינות הבגרות.
כיתה:
כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות.
ידע קודם:
- מציאת אינטגרל על פי זיהוי פונקציה וכפל בנגזרתה.
- חישוב אינטגרל מסוים.
- תכונות של פונקציית מנה.
- מציאת פונקציה קדומה על פי נגזרתה ונקודה עליה.
- סרטוט הפונקציות \(f^3(x)\) , \(\Large\frac{1}{f(x)}\) , מתיחות והזזות שלהן, כאשר נתון גרף הפונקציה \(f(x)\).
מטרות לימודיות:
המשימה מדגישה ידע איכותני – הבנת קשרים ותבניות ולא מתמקדת בטכניקה של מציאת פונקציות קדומות ונגזרות. הדגשים הם:
- התייחסות לתבנית שמתקבלת מגזירת פונקציה מורכבת לפי כלל השרשרת וביצוע פעולה הפוכה – אינטגרציה.
- מציאת תכונות הפונקציה על פי הגרף שלה.
- הבנת התנהגות של פונקציה מורכבת ביחס לפונקציה נתונה, כאשר מפעילים עליה פעולות שונות וסרטוט הגרפים המתאימים.
משימת המטרה:
עוסקת במציאת אינטגרל באמצעות זיהוי פונקציה וכפל בנגזרתה ובפעולות על פונקציה, כאשר הדגש הוא על הגרף של פונקציית מנה ללא הביטוי של הפונקציה.
מדרגה 1:
נתון גרף הפונקציה שיש לה שתי אסימפטוטות מאונכות לצירים ושתי נקודות חיתוך עם ציר ה-\(x\).
מדרגה 2:
נתון גרף פונקציה שיש לה אסימפטוטה אחת (ציר ה-\(x\)) ונקודת חיתוך אחת עם ציר ה-\(x\).
מדרגה 3:
נתונה פונקציה ריבועית והגרף שלה. נתונים גרפים של פונקציות, מהם התלמיד צריך לבחור את המתאימים לפונקציה המתקבלת באינטגרציה.
המדרגות בנויות כך שהן ממקדות את תשומת הלב בנקודות מסוימות בבעיית המטרה. המדרגות נבדלות זו מזו בפונקציות שונות ובכלליות השאלות. ככל שהמדרגה יותר נמוכה הפונקציה יותר פשוטה.
שיטת הוראה:
בכיתה:
תלמידים יעבדו בזוגות, כולם ייחשפו לבעיית המטרה. תוך כדי העבודה בכיתה המורה ינחה את התלמידים להשתמש בבעיות המדרגה, בהתאם להתקדמותם ובהתאם לקשיים שיתקלו במהלך עבודתם, ו/או בהתאם לבקשת התלמידים.
רצוי לערוך דיון כיתתי בו יעלו התלמידים את הקשיים שהיו (בפתרון השאלה) ויציגו את פתרונותיהם ואת התובנות והשיקולים שהנחו אותם בפתרון המשימה.
שימוש ביישומונים:
אין.
שיעורי בית:
סיום המשימה.
משימות מומלצות:
\(f(x)\)
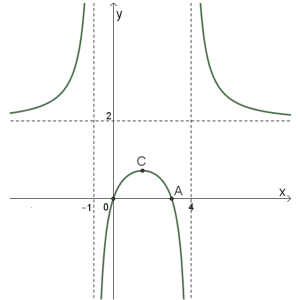
סעיף א
נתון כי: \(h'(x)=f^2(x)\cdot{f'(x)}\)
- חשבו את האינטגרל הבא: \(\int\limits_{1.5}^{a}h'(x)dx\).
- חשבו את האינטגרל הבא: \(\int\limits_{3.5}^{a+2}3\cdot{h'(x-2)}dx\) , נמקו תשובתכם.
- נתון כי הנקודה \((0 ,0)\) נמצאת על גרף הפונקציה \(h(x)\), סרטטו סקיצה של גרף הפונקציה \(h(x)\).
סעיף ב
נסמן נקודה נוספת על גרף הפונקציה \(f(x)\): \(E(e,p)\) כך ש: \(1.5<e<a\).
נתון כי: \(t'(x)=\Large\frac{f'(x)}{f^2{(x)}}\)
- בטאו, באמצעות הנתונים, את האינטגרל הבא: \(\int\limits_{1.5}^{e}t'(x)dx\) .
האם ערך האינטגרל שמצאתם חיובי, שלילי או אפס? נמקו תשובתכם. - נתון כי הנקודה \((1.5 ,-1.389)\) נמצאת על גרף הפונקציה \(t(x)\).
סרטטו סקיצה של גרף הפונקציה \(t(x)\).
- במידת הצורך פתרו את הבעיות במדרגה 1.
\(g(x)\)
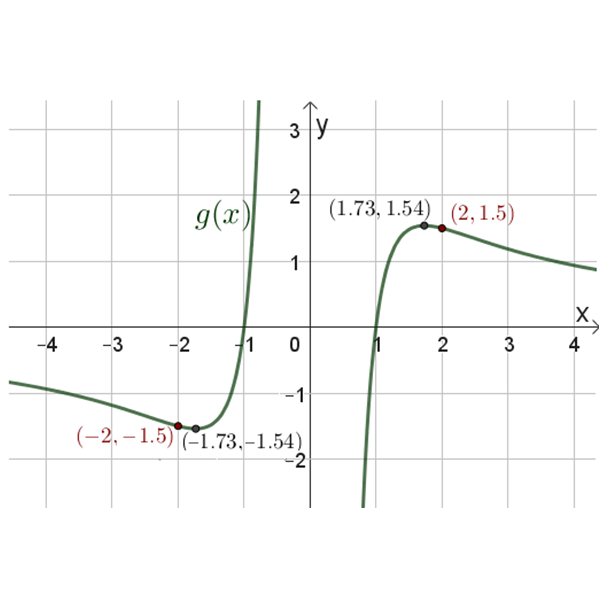
סעיף א
נתון כי: \(p'(x)=g^2(x)\cdot{g'(x)}\)
- חשבו את האינטגרל הבא: \(\int\limits_{-1.73}^{-1}p'(x)dx\).
- נתון כי הפונקציה \(p(x)\) עוברת דרך הנקודה \((1 ,0)\). סרטטו את גרף הפונקציה \(p(x)\).
סעיף ב
נתון: \(m'(x)=\Large\frac{g'(x)}{g^2(x)})\). ונתון כי הנקודה \((1.73 ,-0.65)\) נמצאת על גרף הפונקציה \(m(x)\).
חשבו את \(m(2)\).
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
\(k(x)\)
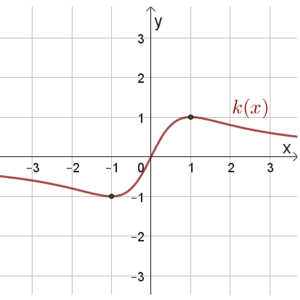
סעיף א
נתון כי: \(n'(x)=k^2(x)\cdot{k'(x})\)
- חשבו את האינטגרל הבא: \(\int\limits_{-1}^{3}n'(x)dx\)
- חשבו את האינטגרל הבא: \(\int\limits_{-2}^{2}n'(x+1)dx\)
סעיף ב
נתון כי: \(m'(x)=\Large\frac{k'(x)}{k^2(x)}\) ונתון כי הנקודה \((1,-1)\) נמצאת על גרף הפונקציה \(m(x)\).
סרטטו את גרף הפונקציה \(m(x)\).
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
\(h(x)\)
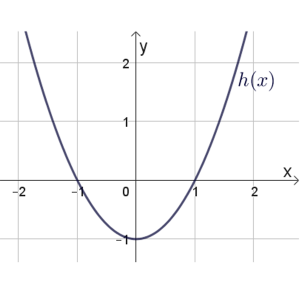
סעיף א
נתון כי: \(p'(x)=h^2(x)\cdot{h'(x)}\)
והנקודה \((0,-\Large\frac{1}{3})\) נמצאת על גרף הפונקציה \(p(x)\).
סרטטו את גרף הפונקציה \(p(x)\).
סעיף ב
נתון כי: \(r'(x)=\Large\frac{h'(x)}{h^2(x)}\). ונתון כי הנקודה \((0,1)\) נמצאת על גרף הפונקציה \(r(x)\).
מצאו איזה גרף מבין הגרפים הנתונים בטבלה מתאים לגרף הפונקציה \(r(x)\). נמקו תשובתכם.
א

ב
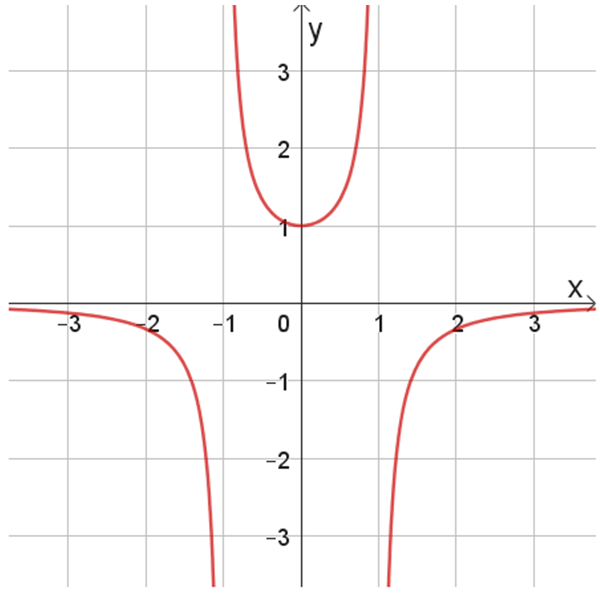
ג
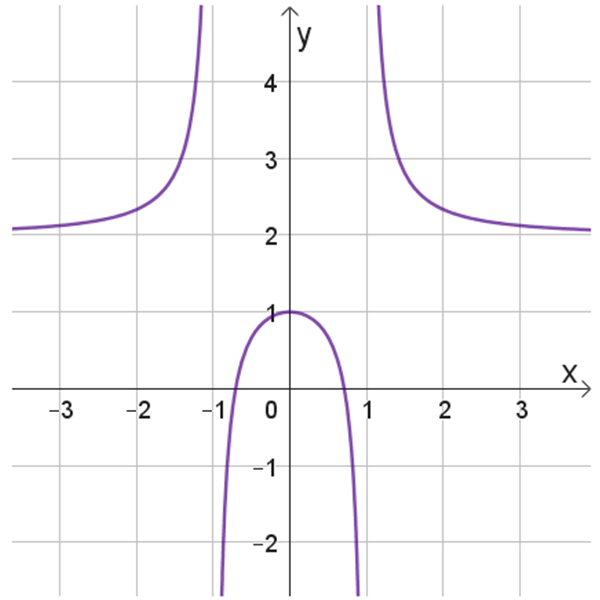
ד

- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















