מקומות גיאומטריים - מי אנחנו? חלק ב' - פרבולה, מעגל, אנך אמצעי - למורה
חומר לימוד:
מציאת משוואות של אנך אמצעי, מעגל ופרבולה לפי תיאור בניה.
כיתה:
כיתה י"ב
מבנה המשימה:
תיאור הבנייה של הפרבולה, כמקום גיאומטרי לא חושף באופן ישיר את סוג העקום. ניתן לפרש את הנתונים ולהסיק שקילות להגדרה המוכרת לפי שוויון מרחקים מנקודה ומישר.
השימוש ביישומונים מציג באופן ברור את המהות של מקום גיאומטרי – אוסף נקודות בעלות תכונה משותפת.
.
ידע קודם:
- נוסחאות למרחק בין נקודות
- מושג האנך האמצעי
- הגדרת הפרבולה
- הגדרת המעגל
מטרות לימודיות:
- הצגת מקומות גיאומטריים באמצעות עקבות בגיאוגברה להמחשת המושג.
- תיאורי הבניה של הפרבולה עלול לפתות לבנות משוואות של ישרים ולמצוא נקודות חיתוך, בהתאם לתהליך פתרון בשאלה רגילה בגיאומטריה אנליטית. בשיטה זו קשה למצוא את הקשר בין שני השיעורים של נקודת החיתוך ולכן קשה למצוא את משוואת המקום המבוקש. מכאן הדוגמא מדגישה את הצורך למצוא תכונה גיאומטרית של הנקודות עבורן מחפשים את המקום הגיאומטרי – תכונה כזו שניתן לתארה במשוואה.
סוג הדירוג:
שלוש מדרגות בשילוב יישומונים.
משימת המטרה:
לקוחה מבחינת הבגרות מס' 035582 קיץ תשע"ח מועד א', ובה שאלות על אנך אמצעי, מעגל ופרבולה.
השאלה כוללת פרמטרים.
מדרגה 1:
שאלה בה מוצגים המרחקים מהנקודה הנתונה ומהישר הנתון באופן ברור. השאלה כוללת פרמטרים. התלמיד יכול למצוא את המקום הגיאומטרי הנדרש בעזרת הגדרת הפרבולה.
מדרגה 2:
בעיה כללית, ללא פתרון מספרי, המרמזת על הגדרת הפרבולה.
מדרגה 3:
בעיה מספרית בה יכול התלמיד למצוא את המקום הגיאומטרי הנדרש בעזרת הגדרת הפרבולה.
שיטת הוראה:
בכיתה:
עבודה בזוגות או בקבוצות. מתחילים מבעיית המטרה ובהתאם לרצון התלמיד או בהכוונת המורה עוברים למדרגות השונות. דיון בכיתה – יש להדגיש את היתרון למצוא תכונה גיאומטרית של הנקודות עבורן מחפשים את המקום הגיאומטרי – תכונה כזו שניתן לתארה במשוואה.
שימוש ביישומונים:
לכל אחת מהמדרגות יש יישומון.
שיעורי בית:
סיום המשימה או פתרון המשימה: מקומות גיאומטריים מי אנחנו? חלק א' – אליפסה ומעגל.
משימות מומלצות:
בעיית מטרה
נתונות הנקודות \(A(-3a,0)\) ו-\(B(3,0)\), \(a>0\) הוא פרמטר.
סעיף א
הביעו באמצעות \(a\) את המקום הגיאומטרי של כל הנקודות \(P\) המקיימות: \(\large\frac{PA}{PB}\normalsize=1\).
סעיף ב
הראו שהמקום הגיאומטרי של כל הנקודות \(Q\) המקיימות: \(\large\frac{QA}{QB}\normalsize=2\) הוא מעגל, והביעו באמצעות \(a\) את שיעורי מרכז המעגל הזה ואת הרדיוס שלו.
סעיף ג
נתבונן באוסף כל המעגלים אשר משיקים למקום הגיאומטרי שמצאתם בסעיף א' ועוברים דרך מרכז המעגל שמצאתם בסעיף ב'.
נתון כי מרכזי המעגלים האלה מהווים מקום גיאומטרי העובר דרך ראשית הצירים.
- זהו את המקום הגיאומטרי הזה.
- מצאו את \(a\), וכתבו את משוואתו של המקום הגיאומטרי הזה.
- במידת הצורך פתרו את הבעיות במדרגה 1.
מדרגה 1
- נתונים הנקודה: \(A(a,0)\), והישר: \(x=(-a)\) , \(a>0\).
בוחרים מספר חיובי \(R>0\).
מסרטטים מעגל ברדיוס \(R\) סביב הנקודה \(A\). מעבירים, מימין לישר \(x=(-a)\), מקביל לו, כך שהמרחק בין המקביל לישר שווה לרדיוס \(R\).
כעת משנים את \(R\).
מצאו את המקום הגיאומטרי של כל הנקודות \(P\) שמתקבלות מחיתוך בין המעגל למקביל. נמקו תשובתכם. - נתונים הנקודה: \(A(a,0)\), והישר: \(x=(-a)\) , \(a>0\).
מסמנים נקודה \(C\) על הישר. מעבירים אנך אמצעי לקטע \(AC\). בנקודה \(C\) מעלים אנך לישר \(x=(-a)\).
מצאו את המקום הגיאומטרי של הנקודות \(P\) שמתקבלות מחיתוך האנך עם האנך האמצעי. נמקו תשובתכם.
השתמשו ביישומון, הזיזו את הנקודה \(C\) וצפו בעקבות של הנקודות \(P\).
חפשו תכונה גיאומטרית שמתארת את מיקומן של הנקודות \(P\). הוכיחו טענתכם.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
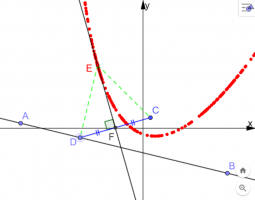
אפיינו את העקום עליו נמצאת הנקודה \(E\): האם הוא מעגל? אליפסה? פרבולה?
אם הוא מעגל – היכן המרכז שלו ומהו אורך הרדיוס שלו?
אם הוא אליפסה – היכן נמצאים מוקדיה? מהו אורך הציר הראשי שלה? נמקו.
אם הוא פרבולה – היכן נמצא המדריך שלה והיכן נמצא המוקד שלה? נמקו.
השתמשו ביישומון: הזיזו את הנקודה \(C\) וצפו בעקבות של הנקודה \(E\).
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- הזיזו את הנקודה \(C\) וצפו בעקבות של הנקודה \(E\).
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
הזיזו את הנקודה \(C\) וצפו בעקבות של הנקודה \(P\).





















