פונקציה לוגריתמית מורכבת – חלק ב – מדרגה 1

פונקציה לוגריתמית מורכבת $ln(f{(x)})$ - חלק ב'

סעיף א

בסרטוט שלפניכם נתון גרף הפונקציה $h(x)$ .

סרטטו את הגרפים של הפונקציות: $ln(h{(x)})$ , $ln(h^2{(x)})$ , $ln(h^3{(x)})$ במערכות צירים נפרדות. נמקו תשובתכם.
האם נכון לטעון כי עבור $h(x)$ הנתונה מתקיים ש: $ln(h^n{(x)})=n\cdot{ln(h(x))}$ , לכל $n$ טבעי? נמקו תשובתכם.

$h(x)$

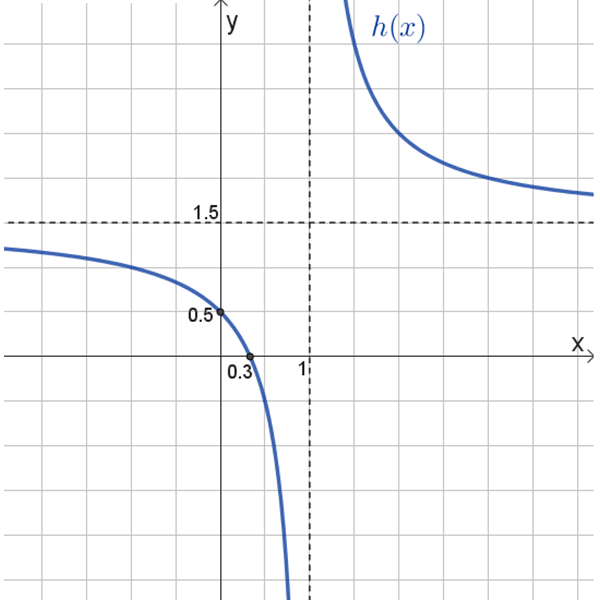
נקודות חיתוך עם הצירים: $(0.3 ,0)$ , $(0 ,0.5)$

אסימפטוטות: $x=1$ , $y=1.5$

סעיף ב

בסרטוט שלפניכם נתון גרף הפונקציה $t(x)$ .

סרטטו את הגרפים של הפונקציות: $ln(t{(x)})$ , $ln(t^2{(x)})$ , $ln(t^3{(x)})$ במערכות צירים נפרדות. נמקו תשובתכם.
האם נכון לטעון כי עבור $t(x)$ הנתונה מתקיים ש: $ln(t^n{(x)})=n\cdot{ln(t(x))}$ , לכל $n$ טבעי? נמקו תשובתכם.

תוכלו להיעזר ביישומון המצורף.

$t(x)$

הפונקציה חותכת את ציר ה- $y$ בנקודה: $(0,0.6)$

נקודת מינימום: $(1,0.5)$

אסימפטוטות: $x=-2$ , $y=1$

יש לבחור את הפונקציה המתאימה ביישומון.
מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
כדי לעבור לפונקציה הלוגריתמית הבאה, יש ללחוץ על החץ בתיבה הכחולה שיופיע בסיום סרטוט תקין.
למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.