נקודת מפגש התיכונים וחותכים אחרים - הוכחות באמצעות שטחים

מדרגה 2

חותכים אחרים דמויי תיכונים (שלישונים)

במשולש \(ABC\) הנקודה \(E\) מחלקת את הצלע \(BC\) כך: \(\large\frac{BE}{BC}\normalsize=\large\frac{1}{3}\).

הנקודה \(D\) מחלקת את הצלע \(AB\) כך: \(\large\frac{BD}{BA}\normalsize=\large\frac{1}{3}\).

הקטעים \(CD\) ו- \(AE\) נחתכים בנקודה \(F\).

bisectors-and-intersectors--pic01a

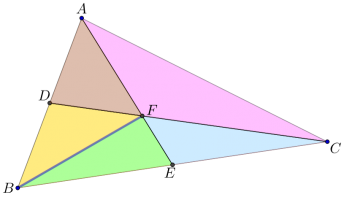
סעיף א

רשמו את היחסים בין השטחים של זוגות המשולשים הבאים:
\(ABE\)    ו- \(AEC\)
\(BDC\)    ו- \(ADC\)
\(ADF\)    ו- \(DBF\)
\(BFE\)    ו- \(CFE\)

סעיף ב

סמנו: \(S_{BDF}=S_1\) , \(S_{BFE}=S_2\)

  1. חשבו מהו היחס בין שטח המשולש \(AFC\) לבין שטח המשולש \(EFC\).
  2. מצאו את היחס בו מחלקת הנקודה \(F\) את הקטעים \(AE\) ו- \(CD\).
  3. הוכיחו כי הנקודה \(F\) נמצאת על התיכון מהנקודה \(B\).
  • אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
  • או, במידת הצורך, פתרו את הבעיות במדרגה 3.

יישומון