משולשים מחוברים בקודקוד - למורה
חומר לימוד:
חקר מצב גיאומטרי בהקשר לקטעי אמצעים במשולש, ובמרובע, תכונות מרובעים וחפיפה ודמיון של משולשים.
בעיה גיאומטרית שמזמנת תרגול תכונות של משפחת המרובעים. שימוש במשפט על קטע אמצעים במשולש ובמרובע. בנוסף, מוצגות שאלות חקר מסוג "מה אם לא?" בהן משתנים נתוני התחלה ונבדקת השפעת השינוי על המסקנה.
ניתן לשלב את המשימה בתחילת כיתה י', או בחזרה לקראת בחינת הבגרות בסיום כיתה י"א. המשימה מתייחסת לתכונות מרובעים וקטע אמצעים במשולש. דמיון המשולשים נדרש רק בהקשר של שוויון הזוויות המתאימות.
כיתה:
כיתה י' / כיתה י"א
מבנה המשימה:
בעיית מטרה, ושלוש בעיות מדרגה. בסוף המשימה (לאחר מדרגה 3), מופיע תרגיל אתגר המיועד לתלמידים שפתרו את בעיית המטרה.
לכל הבעיות מצורפים יישומונים.
ידע קודם:
- חפיפת משולשים
- תכונות מרובעים
- קטע אמצעים במשולש
- דמיון משולשים (הגדרה בלבד)
מטרות לימודיות:
- תרגול תכונות של מרובעים
- תרגול שימוש במשפט על קטע אמצעים
- ביצוע חקירה מתמטית בשיטת "מה אם לא"?– שינוי נתונים ובחינת ההשפעה על המסקנה.
משימת המטרה:
נתונים משולשים שווה שוקיים דומים.
מדרגה 1:
נתון טרפז שווה שוקים, ומרובע המתקבל מחיבור אמצעי צלעותיו.
מדרגה 2:
נתונים משולשים שווי צלעות וגם משולשים שאינם שווי צלעות.
מדרגה 3:
שתי שאלות:
(1) אפיון מרובע המתקבל מחיבור אמצעי צלעותיו של מרובע כלשהו
(2) אפיון מרובע המתקבל מחיבור אמצעי צלעותיו של מרובע שאלכסוניו שווים זה לזה
דרגת המורכבות של השאלות יורדת ממדרגה למדרגה.
שיטת הוראה:
עבודה בכיתה:
עבודה בזוגות או יחידים.
שימוש ביישומונים:
לכל הבעיות מצורפים יישומונים.
שיעורי בית:
סיום המשימה
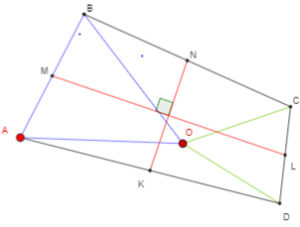
הוכיחו שהקטעים \(ML\) ו-\(KN\) מאונכים זה לזה.
תוכלו להיעזר ביישומון המצורף.
- עיברו לפתרון בעיית האתגר.
- או, במידת הצורך פתרו את הבעיות במדרגה 1.
משולשים שווי שוקיים מחוברים בקודקוד
- גרירת כל אחת מהנקודות האדומות (\(A\) , \(O\)) משנה את הצורה.
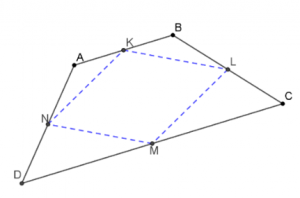
איזה מרובע הוא: \(KLMN\)?
הוכיחו את טענתכם.
תוכלו להיעזר ביישומון המצורף
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- גרירת כל אחת מהנקודות הכחולות (\(C\) , \(D\)) משנה את הצורה.
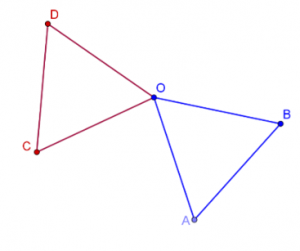
- הוכיחו: \(BC=AD\).
- האם הטענה נשארת נכונה כאשר המשולשים הם שווי צלעות שאינם חופפים זה לזה? הוכיחו טענתכם.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- גרירת כל אחת מהנקודות הכחולות (\(A\) , \(B\) , או הנקודה האדומה \(D\)) משנה את הצורה.
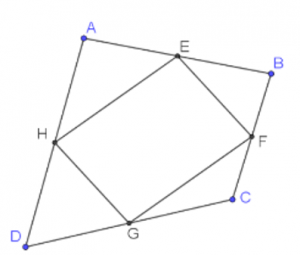
איזה מרובע הוא \(EFGH\)? הוכיחו טענתכם.
- \(ABCD\) הוא מרובע שאלכסוניו שווים באורכם: \(BD=AC\).
הנקודות: \(E\), \(F\), \(G\), \(H\), הן אמצעי הצלעות שלו.
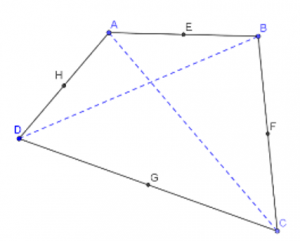
איזה מרובע הוא \(EFGH\)? הוכיחו טענתכם.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
אמצעי הצלעות של מרובע – סעיף 1
- גרירת כל אחת מהנקודות הירוקות (\(A\) , \(B\) , \(C\) , \(D\)) משנה את הצורה.
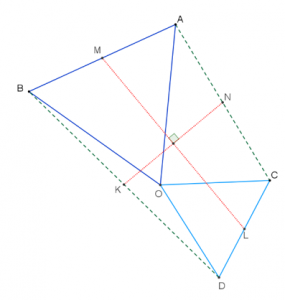
- האם הקטעים \(ML\) ו-\(KN\) יהיו מאונכים זה לזה כאשר המשולשים הם משולשים שווי שוקיים שאינם דומים זה לזה והם מחוברים בקודקוד הראש?
- האם הקטעים יהיו מאונכים זה לזה כאשר המשולשים דומים זה לזה, אך אינם שווי שוקיים?
נמקו טענותיכם.
משולשים שווי שוקיים שאינם דומים
- גרירת כל אחת מהנקודות הכחולות (\(A\) , \(B\) , \(C\)) משנה את הצורה.
משולשים דומים מחוברים בקודקוד מתאים
- גרירת כל אחת מהנקודות האדומות (\(B\) , \(C\) , \(D\)) משנה את הצורה.





















