אינטגרלים: פונקציה ונגזרתה - חלק א' - למורה
חומר לימוד:
סרטוט סקיצה כללית של פונקציה, שהיא פונקציית מכפלה בין פונקציה לנגזרתה:
\(f'(x)\cdot{f(x})\) כאשר נתון רק גרף הנגזרת \(f'(x)\) ונתונים נוספים פרמטריים.
מציאת פונקציה קדומה ל- \(f'(x)\cdot{f(x})\) ושטח הקשור לפונקציה זו בעזרת פרמטרים.
שאלת סיכום בסיום הפרק על אינטגרלים, המתאימה גם לחזרה לקראת בחינות הבגרות.
כיתה:
כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות.
ידע קודם:
- סרטוט גרף פונקציה על פי גרף הנגזרת כאשר לנגזרת ולפונקציה יש אסימפטוטה אופקית.
- מציאת פונקציה קדומה על פי זיהוי פונקציה וכפל בנגזרתה, המביצוע פעולה הפוכה לכלל השרשרת, וחישוב אינטגרל מסוים.
מטרות לימודיות:
במשימה מודגש ידע איכותני ולא טכניקה של אינטגרציה וגזירה. הדגש הוא על:
- קשרים בין גרף פונקציה לנגזרתה
- תכונות של פונקציית מכפלה
- הבנה איכותנית של מציאת אינטגרל ושטח
משימת המטרה:
סרטוט סקיצה כללית של \(f(x)\) ושל \(f'(x)\cdot{f(x})\) כאשר נתון הגרף של \(f'(x)\) ונתונים פרמטריים נוספים.
מדרגה 1:
הפונקציה הנתונה פשוטה יותר ביחס לזו המופיעה במשימת המטרה, עוברת בראשית הצירים.
מדרגה 2:
הפונקציה הנתונה חותכת את ציר ה-\(x\) רק בנקודה אחת, דבר המקל על שירטוט מכפלת הפונקציה בניגזרתה.
מדרגה 3:
מופיע ביטוי מפורש של פונקציה – פרבולה.
שיטת הוראה:
בכיתה:
התלמידים יעבדו בזוגות, הם ייחשפו תחילה לבעיית המטרה. תוך כדי העבודה בכיתה המורה ינחה את התלמידים להשתמש בבעיות המדרגה, בהתאם להתקדמותם, בהתאם לקשיים בהם ייתקלו במהלך עבודתם, ו/או בהתאם לבקשת התלמידים.
רצוי לערוך דיון כיתתי. בדיון יש להדגיש סרטוט סקיצה אפשרית של \(f'(x)\cdot{f(x})\) רק על פי הגרפים של \(f(x)\) ושל \(f('x)\), כלומר סרטוט הסקיצה על פי: נקודות האפס של פונקציית המכפלה, תחומי החיוביות והשליליות שלה והאסימפטוטות האופקיות, וללא מציאת נקודות קיצון וסוגן.
שימוש ביישומונים:
אין.
שיעורי בית:
סיום המשימה.
משימות מומלצות:
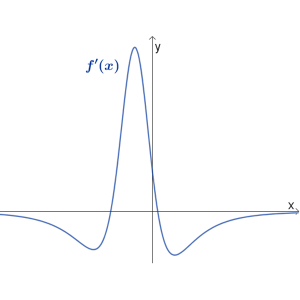
סעיף א
- סרטטו סקיצה של גרף הפונקציה \(f(x)\).
- כמה נקודות חיתוך יש לפונקציה \(f(x)\) עם ציר ה- \(x\)?
סעיף ב
על גרף הפונקציה \(f(x)\) נסמן: נקודת המקסימום \(A(t,k)\), נקודת המינימום \(B(g,p)\).
נגדיר: \(h'(x)=f(x)\cdot{f'(x})\)
- סרטטו סקיצה כללית של גרף הפונקציה \(h'(x)\)
- בטאו את השטח המוגבל בין גרף הפונקציה \(h'(x)\) לבין הישר \(x=g\), הישר \(x=t\) וציר ה-\(x\).
בכל סעיף פרטו ונמקו את תשובתכם.
- במידת הצורך פתרו את הבעיות במדרגה 1.
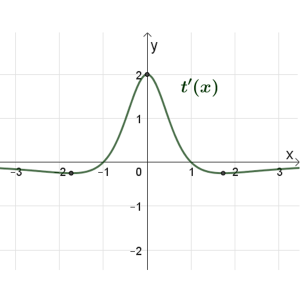
סעיף א
סרטטו את גרף הפונקציה \(t(x)\).
סעיף ב
נתון: \(g'(x)=t(x)\cdot{t'(x})\)
- מצאו מהם תחומי החיוביות והשליליות של הפונקציה \(g'(x)\)
- סרטטו שלוש סקיצות אפשריות לפונקציה: \(g(x)-0.5\cdot{t^2{(x)}}\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
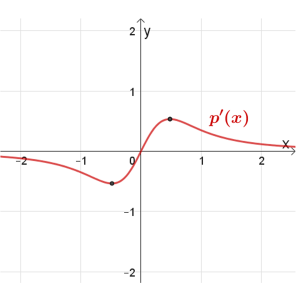
- סרטטו סקיצה של גרף הפונקציה \(p(x)\).
- נתון: \(m'(x)=p(x)\cdot{p'(x})\).
מצאו את תחומי החיוביות והשליליות של הפונקציה \(m'(x)\). - סרטטו סקיצה כללית של הפונקציה \(m'(x)\).
- מצאו את השטח המוגבל בין גרף הפונקציה \(m'(x)\) ובין הישרים \(x=1\) , \(x=0\).
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
מדרגה 3
נתונה הפרבולה \(k(x)=(x-2)(x+3)\).
- סרטטו סקיצה של גרף הפרבולה.
- סרטטו סקיצה של גרף הנגזרת \(k'(x)\).
- נתון כי \(j'(x)=k(x)\cdot{k'(x)}\).
מצאו את נקודות האפס ואת תחומי החיוביות והשליליות של הפונקציה \(j'(x)\). - לפי הגרפים של \(k(x)\) ושל \(k'(x)\) בלבד סרטטו סקיצה כללית של הפונקציה \(j'(x)\) (אין צורך לפתוח סוגריים ואין צורך לגזור).
- אילו ביטויים מבין הביטויים הנתונים למטה יכול להיות ביטוי של הפונקציה \(j(x)\)? נמקו תשובתכם.
א. \(j(x)=(x^2+x)(\Large\frac{x^3}{3}\normalsize+\Large\frac{x^2}{2}\normalsize-6x)\)
\(\space\)
ב. \(j(x)=0.5(x^2+x-6)^2\)
\(\space\)
ג. \(j(x)=\Large\frac{(x^2+x-6)^2+4}{2}\)
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















