פונקציה לוגריתמית מורכבת \(ln(f{(x)})\) - חלק א' - למורה
חומר לימוד:
סרטוט הגרף של הפונקציה \(ln(f{(x)})\), כאשר נתון גרף הפונקציה \(f{(x)}\). משימת סיכום המדגישה את תכונות הפונקציה הלוגריתמית. המשימה מתאימה גם כמשימת סיכום לפני בחינת הבגרות.
כיתה:
כיתה י"ב
מבנה המשימה:
בעיית מטרה, שלוש בעיות מדרגה ובעיית אתגר. לכל אחת מהבעיות מותאמים יישומונים.
ידע קודם:
- הכרת תכונות הפונקציה \(ln(f{(x)})\).
תכונות של פונקציה כמו:
- נקודות חיתוך עם הצירים
- נקודות קיצון וסוגן
- תחומי עליה וירידה
- תחומי חיוביות ושליליות
- אסימפטוטות מקבילות לצירים
- התנהגות פונקציה בקצה תחום הגדרה
מטרות לימודיות:
- אפיון קשרים בין גרף של פונקציה \(f{(x)}\) לבין הגרף של הפונקציה \(ln(f{(x)})\).
- בדיקת הקשרים בלי הכרח להיעזר בנגזרת, כאשר הביטוי של הפונקציה \(f{(x)}\) לא נתון.
משימת המטרה:
נתונה פונקציה בעלת שתי נקודות קיצון, שתי נקודות חיתוך עם ציר ה-\(x\) ושלוש אסימפטוטות, שתיים אנכיות ואחת אופקית.
משימת אתגר:
חקר דומה לזה של משימת המטרה על פונקציה חיובית בעלת אסימפטוטה אופקית ונקודת קיצון ועל הזזה שלה ביחס לציר \(y\).
מדרגה 1:
נתונים גרפים של שתי פונקציות לאחת יש 3 נקודות קיצון ולשניה יש אסימפטוטה אנכית, אסימפטוטה אופקית ונקודת קיצון אחת. על התלמיד לסרטט את הגרפים של \(ln(f{(x)})\).
מדרגה 2:
נתונים שלושה גרפים \(g{(x)}\) של פונקציות פשוטות (שתי פרבולות והזזה של \(\Large\frac{1}{x}\)). על התלמיד לסרטט את הגרפים של \(ln(g{(x)})\).
מדרגה 3:
נתונים שלושה גרפים \(f{(x)}\) , \(h{(x)}\) , \(t{(x)}\) וארבעה גרפים ביניהם צריך לבחור את המתאימים לפונקציות: \(ln(f{(x)})\) , \(ln(h{(x)})\) , \(ln(t{(x)})\).
שיטת הוראה:
בכיתה:
התלמידים יעבדו בזוגות, תוך כדי העבודה בכיתה המורה ינחה את התלמידים להשתמש בבעיות המדרגה, בהתאם להתקדמותם, בהתאם לקשיים בהם ייתקלו במהלך עבודתם, ו/או בהתאם לבקשת התלמידים.
שימוש ביישומונים:
בכל בעיה ובכל שלב השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה, והגיע למסקנות הנדרשות. רצוי שתלמיד יסרטט את הגרפים המבוקשים במחברתו. חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
הערה:
אין צורך להיעזר בנגזרות, אלא להיעזר בתכונה הבאה: כיוון שהפונקציה \(ln(x)\) היא פונקציה עולה, הרי שבתחום בו \(f(x)\) עולה ו-\(ln(f{(x)})\) מוגדרת, גם \(ln(f{(x)})\) עולה. בתחום בו \(f(x)\) יורדת ו-\(ln(f{(x)})\) מוגדרת, גם \(ln(f{(x)})\) יורדת.
משימות מומלצות:
\(f{(x)}\)
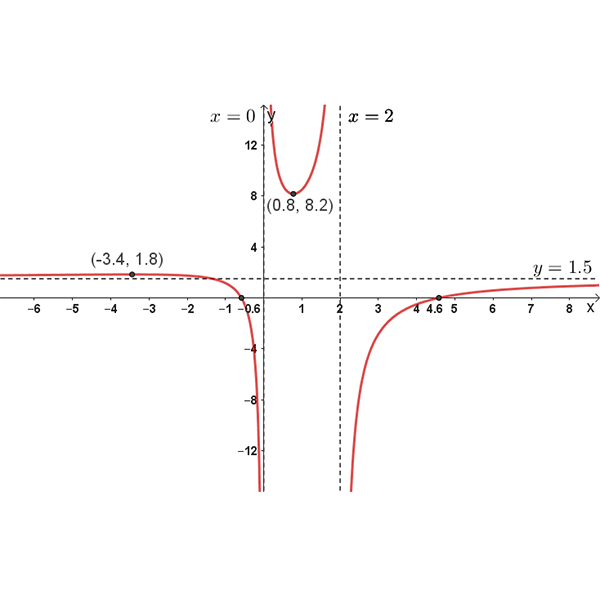
נקודות חיתוך עם הצירים: \((4.6 ,0)\) , \((-0.6 ,0)\)
נקודות קיצון: \((0.8 ,8.2)\) , \((-3.4 ,1.8)\)
אסימפטוטות: \(x=2\) , \(x=0\) , \(y=1.5\)
- במידת הצורך פתרו את הבעיות במדרגה 1.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
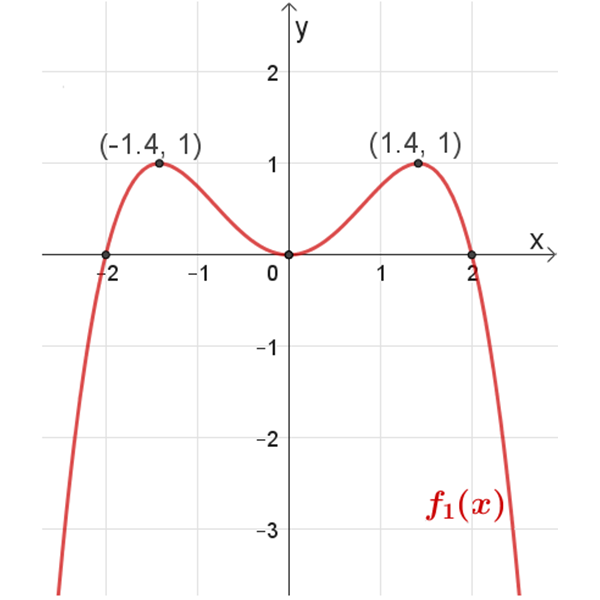
\(f_1{(x)}\)
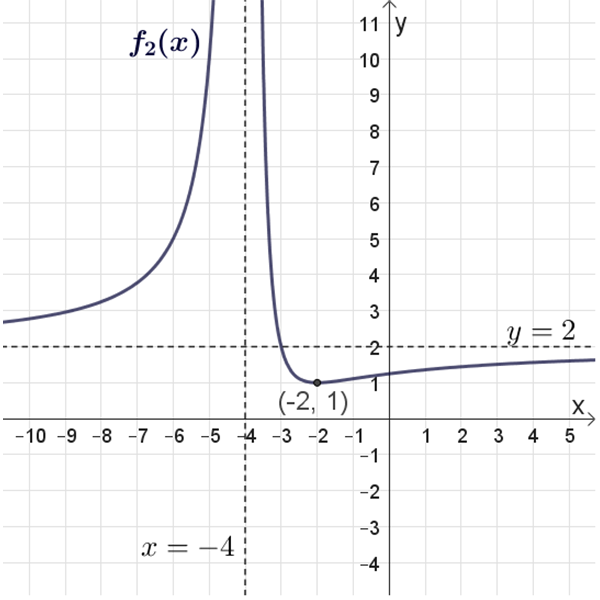
\(f_2{(x)}\)
נקודות חיתוך עם הצירים: \((2 ,0)\) , \((0 ,0)\) , \((-2,0)\)
נקודות קיצון: \((1.4 ,1)\) , \((0,0)\) , \((-1.4 ,1)\)
נקודת חיתוך עם הצירים: \((0 ,1.25)\)
נקודת קיצון: \((-2 ,1)\)
אסימפטוטות: \(x=-4\) , \(y=2\)
תוכלו לסרטט ולבדוק תשובותיכם ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
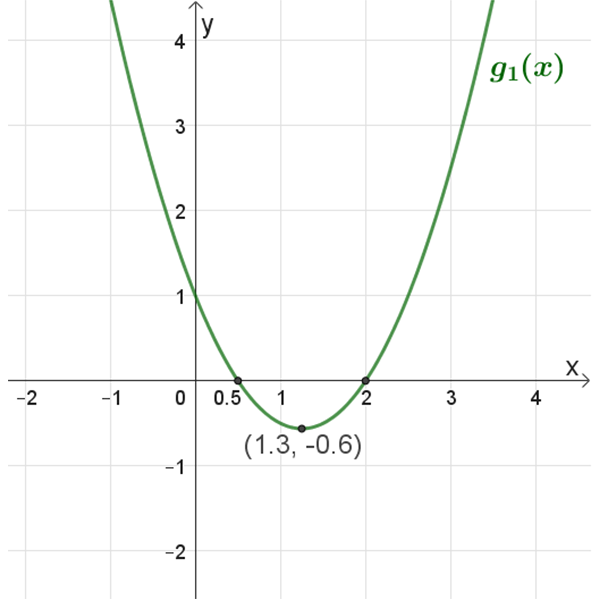
\(g_1{(x)}\)
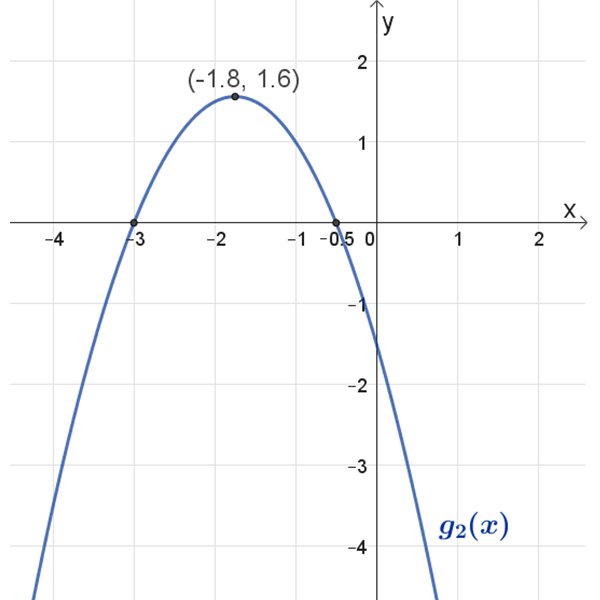
\(g_2{(x)}\)
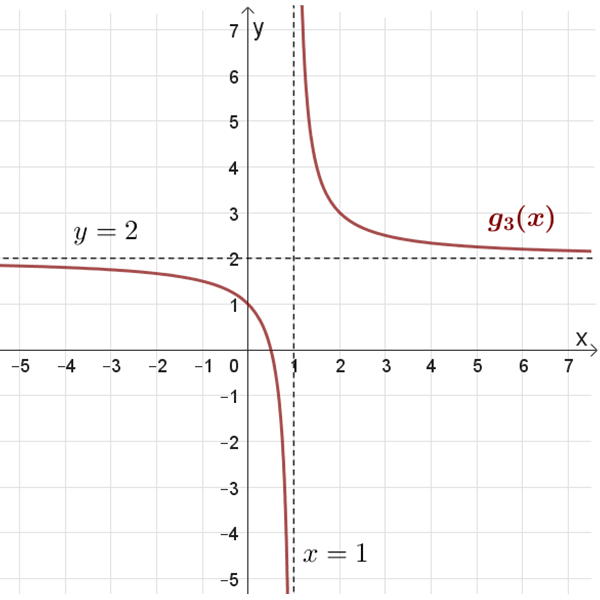
\(g_3{(x)}\)
נקודות חיתוך עם הצירים: \((2 ,0)\) , \((0.5 ,0)\) , \((0,1)\)
נקודת קיצון: \((1.3,-0.6)\)
נקודות חיתוך עם הצירים: \((0 ,-1.5)\) , \((-0.5 ,0)\) , \((-3,0)\)
נקודת קיצון: \((-1.8,1.6)\)
נקודות חיתוך עם הצירים: \((0.5 ,0)\) , \((0,1)\)
אסימפטוטות: \(x=1\) , \(y=2\)
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
גרפים של פונקציות נתונות:
\(f(x)\)
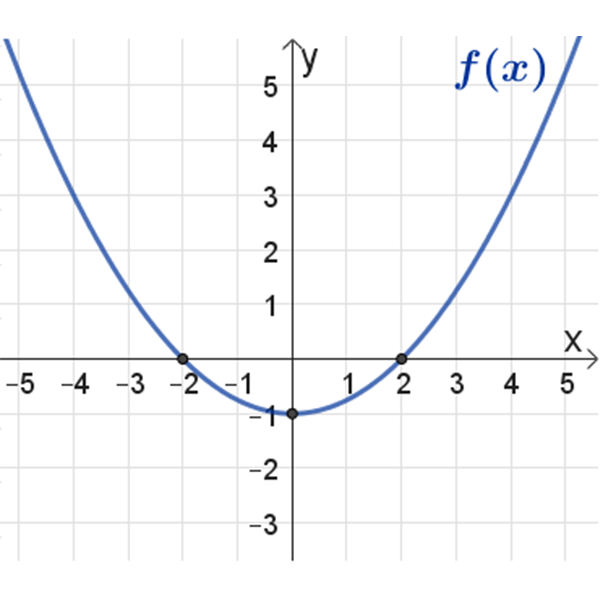
\(h(x)\)
\(t(x)\)
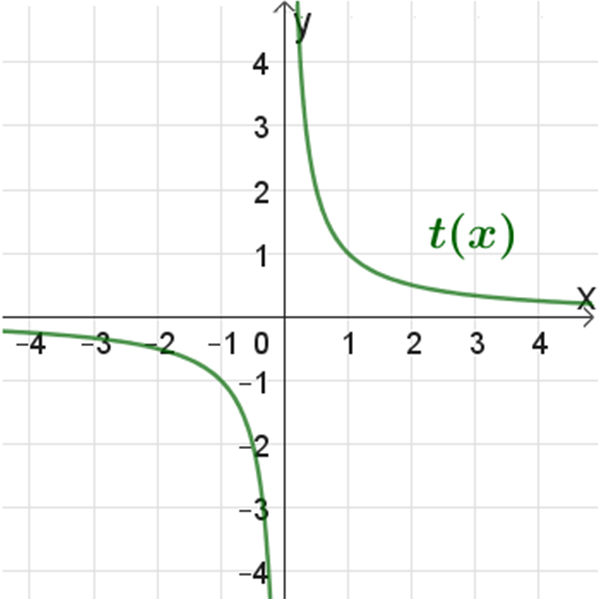
גרפים של פונקציות לוגריתמיות:
1
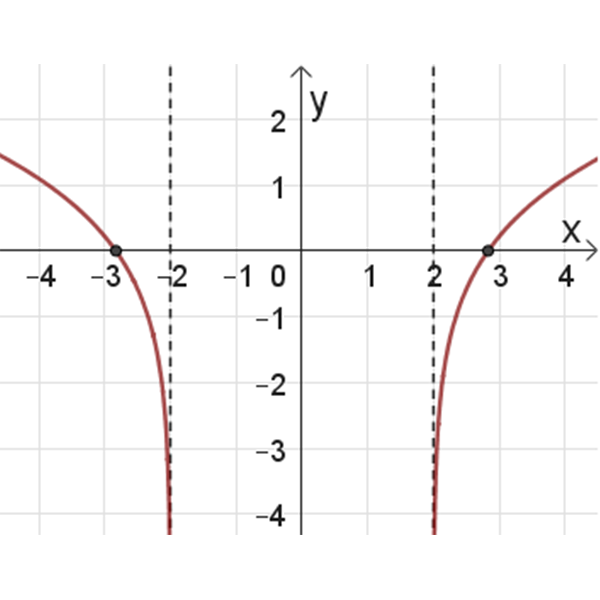
2
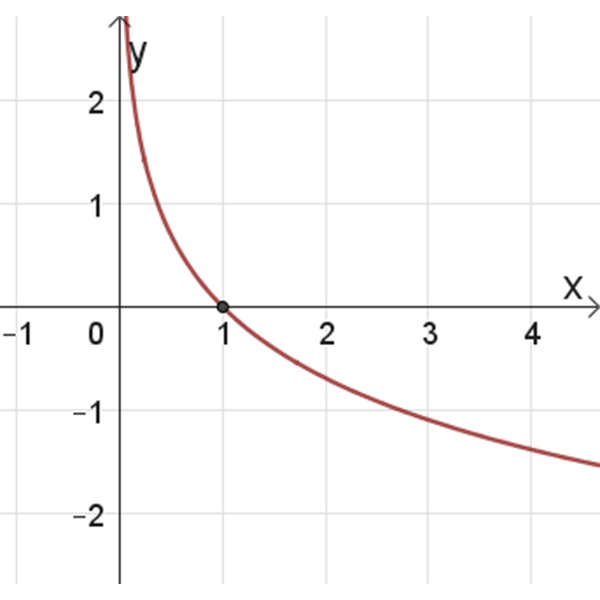
3
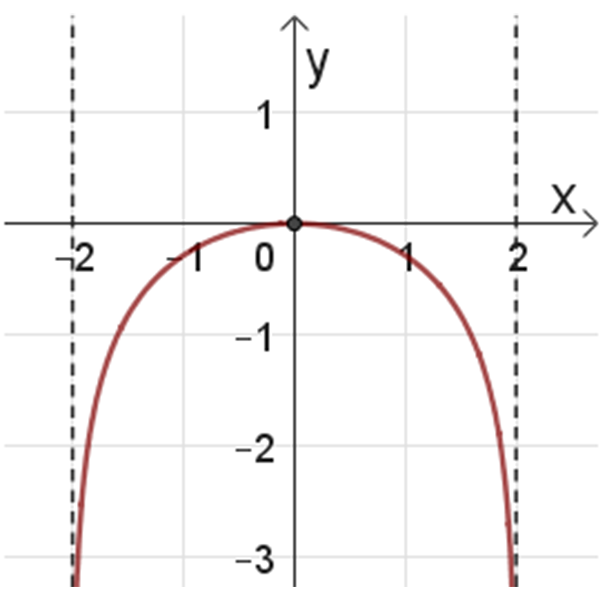
4
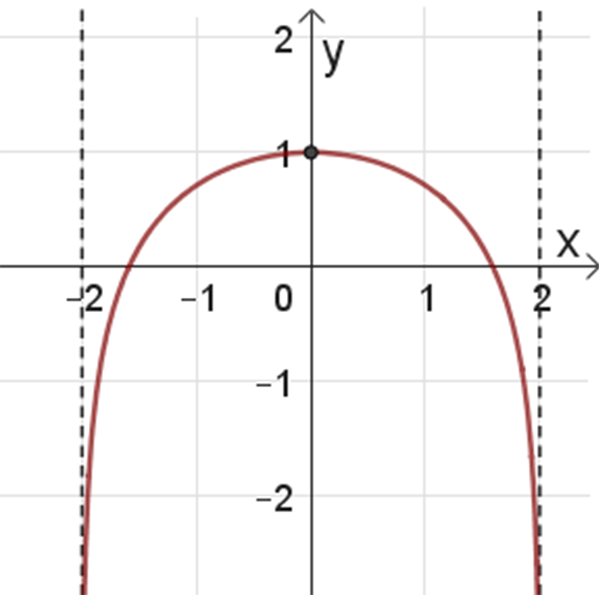
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
כדי להציג פרבולה, בחרו את \(h(x)\):
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה האדומה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה, על מנת להחליף בין \(h(x)\) ו-\(f(x)\)
כדי להציג היפרבולה, בחרו את \(t(x)\):
- ניתן להזיז את ההיפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה האדומה.