פעולות על פונקציה - למורה
חומר לימוד:
ייצוג גרפי של פונקציות מורכבות: \(\Large\frac{1}{f(x)}\) , \(\sqrt{f(x)}\) , \(f^2(x)\) , \(|f(x)|\) , \(f(-x)\) , \(-f(x)\)
כיתה:
כיתה י' / כיתה י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות. ישנם יישומונים לבעיית המטרה ולכל אחת מהמדרגות.
ידע קודם:
תכונות של פונקציות: תחום הגדרה, נקודות חיתוך עם הצירים, תחומי חיוביות שליליות, נקודות קיצון וסוגן, תחומי עליה וירידה, אסימפטוטות מקבילות לצירים, נקודות אי רציפות סליקה. פונקציית ערך מוחלט, פונקציה נגדית, פונקציה הופכית, פונקציית השורש הריבועי. סרטוט גרפים.
נגזרות של: פונקציית שורש ריבועי, פונקציית מנה, פונקציה מורכבת (לא הכרחי).
אין התייחסות מפורשת במשימה זו לנקודות פיתול.
מטרות לימודיות:
אפשר להשתמש במשימה: בכיתה י"א, לאחר סיום הוראת החשבון הדיפרנציאלי.
או בכיתה י' כהקדמה לחדו"א, אחרי שלומדים על פונקציה נגדית, פונקציה הופכית, פונקציית הערך המוחלט, פונקציית שורש ריבועי. ואחרי שלומדים על אסימפטוטות מקבילות לצירים – אין צורך בנגזרות לביצוע המשימה. אפשר להסתמך על תכונות של מספרים.
המשימה מתמקדת ביידע איכותני ולא בטכניקה של מציאת נגזרות ופתרון משוואות.
המשימה שמה דגש על:
- הבנת התנהגות של פונקציה מורכבת ביחס לפונקציה נתונה, כאשר מפעילים עליה את הפעולות הבאות: שיקוף באחד מן הצירים, ערך מוחלט, העלאה בריבוע, שורש ריבועי, פונקציה הופכית.
- השונה והדומה בין הפעולות הנ"ל.
- בדיקת המצב ההדדי בין פונקציה נתונה ובין הרכָּבָה שלה כנ"ל.
משימת המטרה:
מופיע גרף של פונקציית מנה עם אסימפטוטה אופקית ושתי אסימפטוטות אנכיות, שתי נקודות קיצון ושתי נקודות חיתוך עם ציר ה-\(x\).
למשימה ששה סעיפים. בכל סעיף יש לסרטט גרף, המתקבל כתוצאה מפעולה מסוימת על הגרף הנתון.
יש למיין את הגרפים השונים המתקבלים במשימה בדרכים שונות.
המדרגות מאופיינות על ידי גרפים של פונקציות פשוטות יותר.
מדרגה 1:
מופיע גרף של פונקציה עם אסימפטוטה אופקית אחת ואסימפטוטה אנכית אחת. ושתי נקודות חיתוך עם ציר ה-\(x\).
מדרגה 2:
מופיע גרף של פונקציה עם אסימפטוטה אופקית אחת, שתי נקודות קיצון ונקודת חיתוך אחת עם הצירים.
מדרגה 3:
פרבולה בעלת נקודת מקסימום ושתי נקודות חיתוך עם ציר ה-\(x\).
שיטת הוראה:
עבודה בזוגות. תלמידים המתקשים בסעיף מסוים בבעיית המטרה יכולים לעבור מדרגה ולפתור את אותו סעיף עבור פונקציה פשוטה יותר.
בכיתה:
דיון כיתתי: הצגת דרכים שונות למיון הגרפים שהתקבלו על ידי התלמידים. לדוגמא: מיון לפי תחום הגדרה של הפונקציות, מיון לפי מספר נקודות קיצון של הפונקציות, מיון לפי תחומי חיוביות/שליליות של הפונקציות וכו'. רצוי להיעזר ביישומון המצורף.
שיעורי הבית:
השלמת המשימה אם יש צורך. ניתן לבקש מהתלמידים לפתור את המשימות במדרגות השונות.
שימוש ביישומונים:
לבעיית המטרה ולכל מדרגה יישומונים שונים בהתאם לפונקציה הנתונה.
בכל בעיה ובכל שלב השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה והגיע למסקנות הנידרשות. אם תלמיד טעה / או לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
הערות נוספות למורה:
בדיון בכיתה רצוי להבהיר שניתן להגיע לכל הגרפים הנדרשים ללא שימוש בנגזרת, יחד עם זאת רצוי לקשר ולהראות איך הנגזרת מספקת מידע אליו ניתן להגיע גם בעזרת שיקולים אחרים הקשורים לתכונות של מספרים.
יש לשים לב לנקודות אי רציפות סליקה המתקבלות בפונקציה הופכית \(\Large\frac{1}{f(x)}\) בנקודות בהן לפונקציה \(f(x)\) יש אסימפטוטה אנכית.
ניתן להתאים את המשימה לפונקציות שונות, ובכך לשנות את רמתה, וכן לאפשר תרגול נוסף לתלמידים הזקוקים לכך.
הצעות לפונקציות נוספות: \(f(x)=\Large\frac{4x-4}{(x-2)^2}\) , \(f(x)=4-\Large\frac{4}{(x-2)^2}\) , \(f(x)=\Large\frac{2-x}{x^2-4x+5}\) , \(f(x)=(x-2)^2\) , \(f(x)=\Large\frac{2}{9}\normalsize\cdot(x-1)\cdot(4-x)\)
כמו כן ניתן להתאים את המשימה לפונקציות טריגונומטריות, לפונקציות מעריכיות, לוגריתמיות או לפונקציות שמכילות שורשים בהתאם לשלבי הלימוד המתאימים.
ניתן להרכיב פונקציות נוספות כגון: \(f^3(x)\) , \(f({\Large\frac{1}{x}})\).
ניתן להוסיף ולבקש לסרטט גם את הגרפים של הנגזרות בסעיפים השונים.
\(f{(x)}\)
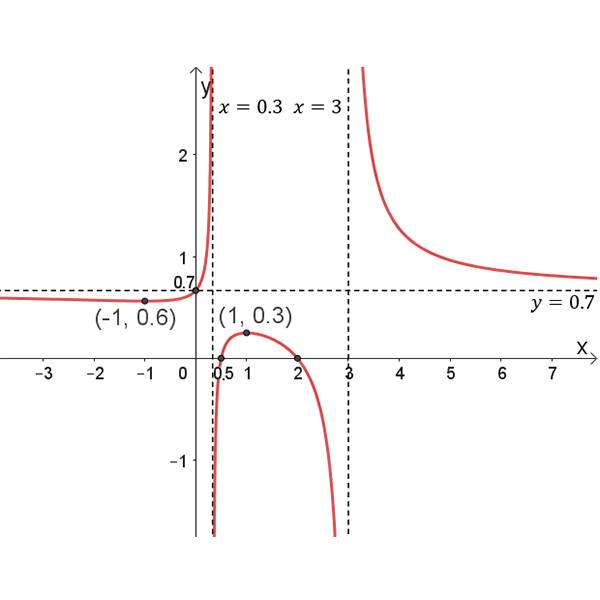
נקודות חיתוך עם הצירים: \((0.5 ,0)\) , \((2 ,0)\) , \((0 ,0.7)\)
אסימפטוטות מאונכות לצירים: \(y=0.7\) , \(x=0.3\) , \(x=3\)
נקודות הקיצון: \((1 ,0.3)\) , \((-1 ,0.6)\)
סעיף א
סרטטו סקיצה של גרף הפונקציה המתקבלת מכל אחת מהפעולות הבאות:
א. \(-f(x)\) ב. \(f(-x)\)
ג. \(|f(x)|\) ד. \(f^2(x)\)
ה. \(\sqrt{f(x)}\) ו. \(\Large\frac{1}{f(x)}\)
תוכלו להיעזר ביישומון המצורף ולבדוק תשובותיכם.
סעיף ב
מיינו בדרכים שונות את הגרפים שהתקבלו בסעיפים א-ו.
(לדוגמה, מיון לפי התכונה: תחום הגדרה של הגרף שהתקבל)
- במידת הצורך פתרו את הבעיות במדרגה 1.
- ניתן לבחור את הפעולה הרצויה על הפונקציה, ע"י לחיצה על הכפתור הירוק ("שנה פעולה"), בתפריט שבתחתית היישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן: כחולות מלאות ו/או ירוקות ריקות (אם יש צורך, לסימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי סימון "אסימפטוטות" מתאימות, בתפריט שבתחתית היישומון. ולאחר מכן, למקם את האסימפטוטה על ידי גרירת הנקודה הצהובה שעליה.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפעולה הבאה יש ללחוץ על שנה פעולה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- לצורך מיון הפונקציות ובדיקת המצבים ההדדיים בין הגרפים המתקבלים, ניתן ביישומון זה לראות כמה גרפים בו זמנית על ידי בחירת הביטויים האלגבריים של הפונקציות המופיעים מימין.
\(g{(x)}\)
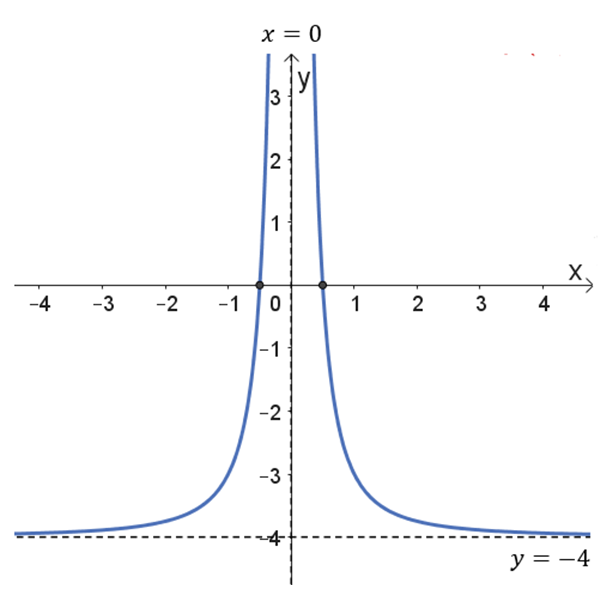
נקודות חיתוך עם ציר ה-\(x\): \((0.5 ,0)\) , \((-0.5,0)\)
אסימפטוטות מאונכות לצירים: \(y=-4\) , \(x=0\)
סרטטו סקיצה של גרף הפונקציה המתקבלת מכל אחת מהפעולות הבאות:
א. \(-g(x)\) ב. \(g(-x)\)
ג. \(|g(x)|\) ד. \(g^2(x)\)
ה. \(\sqrt{g(x)}\) ו. \(\Large\frac{1}{g(x)}\)
תוכלו לסרטט ולבדוק תשובותיכם ביישומון המצורף. אם טעיתם, חישבו מה מקור הטעות.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- ניתן לבחור את הפעולה הרצויה על הפונקציה, ע"י לחיצה על הכפתור הירוק ("שנה פעולה"), בתפריט שבתחתית היישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן: כחולות מלאות ו/או ירוקות ריקות (אם יש צורך, לסימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי סימון "אסימפטוטות" מתאימות, בתפריט שבתחתית היישומון. ולאחר מכן, למקם את האסימפטוטה על ידי גרירת הנקודה הצהובה שעליה.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפעולה הבאה יש ללחוץ על שנה פעולה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
\(h{(x)}\)
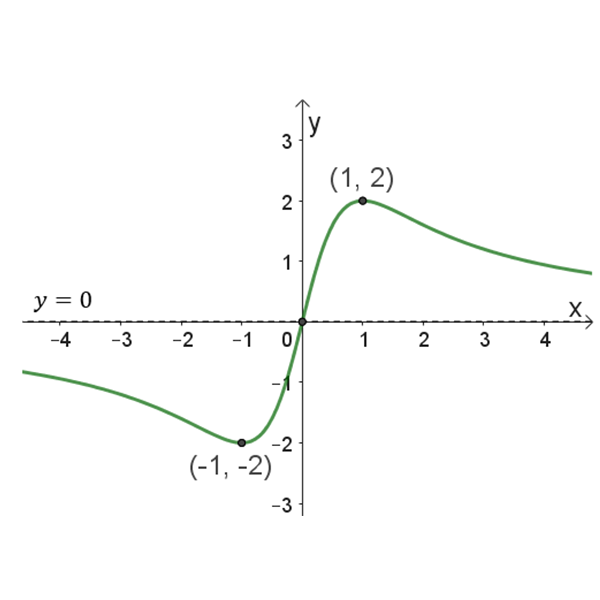
הפונקציה חותכת את הצירים בנקודה: \((0,0)\)
נקודות קיצון: \((1 ,2)\) , \((-1,-2)\)
אסימפטוטה אופקית: \(y=0\)
סרטטו סקיצה של גרף הפונקציה המתקבלת מכל אחת מהפעולות הבאות:
א. \(-h(x)\) ב. \(h(-x)\)
ג. \(|h(x)|\) ד. \(h^2(x)\)
ה. \(\sqrt{h(x)}\) ו. \(\Large\frac{1}{h(x)}\)
תוכלו להיעזר ביישומון המצורף ולבדוק תשובותיכם. אם טעיתם, חישבו מה מקור הטעות.
בסרטוט הסקיצה שימו לב גם ל:
- נקודות חיתוך בין גרף הפונקציה \(h(x)\) לגרף הפונקציה המתקבל בכל אחד מהסעיפים,
- ולמצב הדדי בין גרף הפונקציה \(h(x)\) לגרף הפונקציה המתקבל בכל אחד מהסעיפים.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- ניתן לבחור את הפעולה הרצויה על הפונקציה, ע"י לחיצה על הכפתור הירוק ("שנה פעולה"), בתפריט שבתחתית היישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן: כחולות מלאות ו/או ירוקות ריקות (אם יש צורך, לסימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי סימון "אסימפטוטות" מתאימות, בתפריט שבתחתית היישומון. ולאחר מכן, למקם את האסימפטוטה על ידי גרירת הנקודה הצהובה שעליה.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפעולה הבאה יש ללחוץ על שנה פעולה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
\(p(x)\)
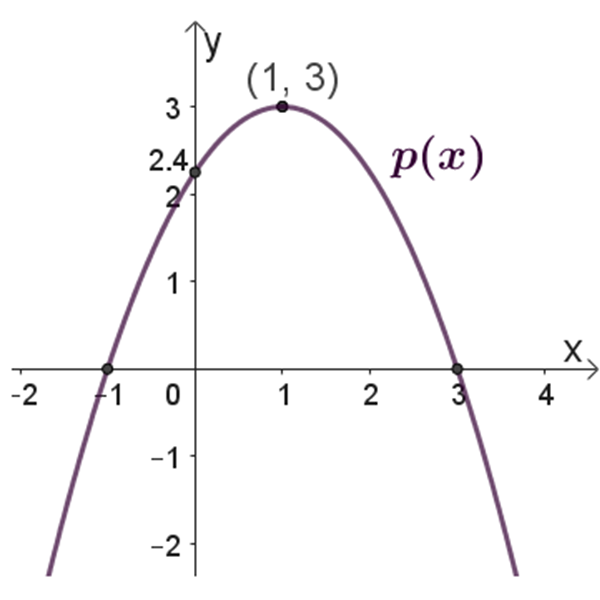
הפונקציה חותכת את ציר ה-\(x\) בנקודות: \((-1,0)\) , \((3,0)\)
הפונקציה חותכת את ציר ה-\(y\) בנקודה: \((0 ,2.4)\)
נקודת קיצון: \((1 ,3)\)
סרטטו סקיצה של גרף הפונקציה המתקבלת מכל אחת מהפעולות הבאות:
א. \(-p(x)\) ב. \(p(-x)\)
ג. \(|p(x)|\) ד. \(p^2(x)\)
ה. \(\sqrt{p(x)}\) ו. \(\Large\frac{1}{p(x)}\)
תוכלו להיעזר ביישומון המצורף ולבדוק תשובותיכם. אם טעיתם, חישבו מה מקור הטעות.
בסרטוט הסקיצה שימו לב גם ל:
- נקודות חיתוך בין גרף הפונקציה \(p(x)\) לגרף הפונקציה המתקבל בכל אחד מהסעיפים,
- ולמצב הדדי בין גרף הפונקציה \(p(x)\) לגרף הפונקציה המתקבל בכל אחד מהסעיפים.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- ניתן לבחור את הפעולה הרצויה על הפונקציה, ע"י לחיצה על הכפתור הירוק ("שנה פעולה"), בתפריט שבתחתית היישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן: כחולות מלאות ו/או ירוקות ריקות (אם יש צורך, לסימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי סימון "אסימפטוטות" מתאימות, בתפריט שבתחתית היישומון. ולאחר מכן, למקם את האסימפטוטה על ידי גרירת הנקודה הצהובה שעליה.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפעולה הבאה יש ללחוץ על שנה פעולה.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).





















