הוכחות באמצעות שטחים - תכונת חוצה הזווית במשולש - למורה

משימה לתלמיד

דף למורה

מבנה המשימה

יישומונים

  • – – – – –

חומר לימוד:

הוכחות באמצעות שטחים לתכונת חוצה הזווית במשולש. המשימה מנחה להוכיח את המשפט באמצעות שיקולים של השוואת שטחים, שיטה יעילה ונדרשת בפתרון משימות הוכחה וחישוב בגיאומטריה.

משימה זו היא אחת משלוש משימות שמכוונות לשימוש בשיטה זו – המשפט על נקודת מפגש התיכונים, משפט תאלס, המשפט ההפוך לו ותכונת חוצה הזווית.

כיתה: 

כיתה י'

מבנה המשימה:

בעיית מטרה אחת, ושלוש מדרגות.

ידע קודם:                     

  • שטח משולש
  • הגדרה של מרחק נקודה מישר

מטרות לימודיות:          

  • הוכחת משפט מרכזי בתכנית הלימודים בדרך פשוטה.
  • תרגול השימוש בשיקולים של חישובי שטחים – שיקולים שנדרשים בשאלות אחרות.

משימת המטרה:

הוכחת משפט חוצה זווית פנימית במשולש.

מדרגה 1:

הוכחת החפיפה בין משולשים שנוצרו על ידי הורדת אנך מנקודת החיתוך של חוצה הזווית עם הצלע שמולו לצלעות הנותרות במשולש.

מדרגה 2:

השוואת היחס בין שטחי משולשים שחוצה הזווית במשולש יוצר ליחס בין הצלעות שהן שוקי הזווית הנחצית.

מדרגה 3:

מציאת יחס השטחים שיוצר קטע המחבר את קודקוד הזווית עם הצלע שמולו.

שיטת הוראה:

בכיתה:

עבודה, עצמאית או בזוגות, התלמידים יעברו בין המדרגות השונות ביוזמתם או בהדרכת המורה.

כל התלמידים יתמודדו עם הוכחת המשפט המופיע בתכנית הלימודים.

שימוש ביישומונים: אין

שיעורי בית:

תלמידים שלא פתרו את בעיית המטרה בכיתה ישלימו את עבודתם בבית.

הערה:

ההוכחה באמצעות שטחים מראה שניתן להציג את המשפט עוד לפני משפט תאלס.

משימות מומלצות:

בעיית מטרה

הוכיחו את המשפט:

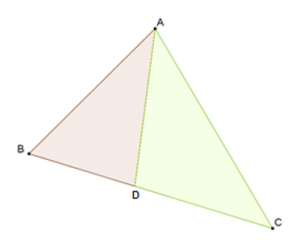
חוצה הזווית במשולש מחלק את הצלע אותה הוא חותך לשני קטעים המתייחסים זה לזה כיחס בין שתי הצלעות האחרות, כלומר:

במשולש \(ABC\), הקטע \(AD\) הוא חוצה הזווית \(\measuredangle BAC\).

יש להוכיח כי:  \(\Large\frac{AB}{AC}\normalsize=\Large\frac{BD}{DC}\)

  • במידת הצורך, פתרו את הבעיות במדרגה 1.

מדרגה 1

בסרטוט נתון המשולש ABC.  \(AD\) חוצה את הזווית \(\measuredangle BAC\).

מ \(D\) הורידו אנך \(DG\) לצלע \(AB\) , ואנך \(DH\) לצלע \(AC\).

הוכיחו כי: \(\triangle AGD \cong \triangle AHD\).

  • אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
  • או, במידת הצורך, פתרו את הבעיות במדרגה 2.

מדרגה 2

בסרטוט נתון המשולש ABC. \(D\) נקודה על \(BC\).

נתון: \(\Large\frac{S_{\triangle ABD}}{S_{\triangle ACD}}\normalsize=\Large\frac{AB}{AC}\)

הוכיחו:  \(\Large\frac{AB}{AC}\normalsize=\Large\frac{BD}{DC}\)

  • אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
  • או, במידת הצורך, פתרו את הבעיות במדרגה 3.

מדרגה 3

בסרטוט נתון המשולש ABC. \(D\) נקודה על הצלע \(BC\).

הוכיחו: \(\Large\frac{S_{\triangle ABD}}{S_{\triangle ACD}}\normalsize=\Large\frac{BD}{DC}\)