חזקה טבעית של פונקציה - חלק ג' - \(f^n{(x)}\) - למורה
חומר לימוד:
המשותף והשונה בין הפונקציות \(f^2(x)\) ו- \(f^3(x)\). משימה זו משלבת בין ידע שנרכש בחלק א' לבין זה שנרכש בחלק ב'.
כיתה:
כיתה י'
מבנה המשימה:
בעיית מטרה, שלה מותאמים שלוש בעיות מדרגה. לכל הבעיות מצורפים יישומונים.
ידע קודם:
- אפיון קשרים בין גרף של פונקציית פולינום \(f(x)\) לבין גרף הפונקציה \(f^2(x)\).
- אפיון קשרים בין גרף של פונקציית פולינום \(f(x)\) לבין גרף הפונקציה \(f^3(x)\).
משימה זו מקומה לאחר משימות: "חזקה טבעית של פונקציה – חלק א – חזקה שניה", ו"חזקה טבעית של פונקציה – חלק ב – חזקה שלישית".
מטרות לימודיות:
- אפיון המצב ההדדי בין הפונקציות \(f(x)\) , \(f^2(x)\) ו-\(f^3(x)\)
- זיהוי נקודות פיתול בהן שיפוע המשיק הוא אפס, בנקודות האפס של הגרף \(f^3(x)\).
סוג הדירוג:
שלוש מדרגות: הגרפים הנתונים בכל בעיית מדרגה מכילים פחות נקודות חיתוך ופחות נקודות קיצון מאשר הגרף בבעיית המטרה ובמדרגה הקודמת.
משימת המטרה:
פונקציה ולה יש שלוש נקודות חיתוך עם ציר ה-\(x\) ושתי נקודות קיצון: באחת \(|y|<1\) ובשניה \(|y|>1\).
מדרגה 1:
פונקציה סימטרית לגבי ציר ה-\(y\), משיקה לציר ה-\(x\). לפונקציה שלוש נקודות קיצון ושלוש נקודות חיתוך עם ציר ה-\(x\).
מדרגה 2:
פרבולה קעורה כלפי מטה.
מדרגה 3:
קו ישר.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. רצוי להיעזר ביישומונים המצורפים.
שימוש ביישומונים:
בכל בעיה ובכל שלב השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה והגיע למסקנות הנידרשות. אם תלמיד טעה / או לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
שיעורי בית:
סיום המשימה. אפשר לעבור לחלק ד'.
משימות מומלצות:
משימות קודמות:
משימה נוספת בנושא זה:
\(f(x)\)
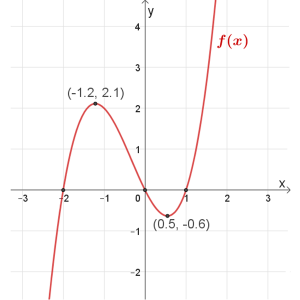
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-2,0)\)
נקודות קיצון: מקסימום \((-1.2,2.1)\) , מינימום \((0.5,-0.6)\)
- סרטטו באותה מערכת צירים, בצבעים שונים, את הגרפים של:
א. \(f^3(x)\)
ב. \(f^2(x)\) - באיזה תחום \(f^3(x)\le{f^2(x)}\)? (דייקו בתשובתכם ככל האפשר).
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף. - לאיזו פונקציה מבין הפונקציות \(f^3(x)\) , \(f^2(x)\), \(f(x)\) יש נקודות פיתול בהן שיפוע המשיק הוא אפס?
מה הם שיעורי נקודות אלה?
- במידת הצורך פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) ולפחות שבע נקודות צהובות (לסרטוט \(f^3(x)\)), במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- כדי "לנקות" את היישומון ולהתחיל מחדש עם הפונקציה המוצגת, ניתן ללחוץ על אתחול.
\(h(x)\)
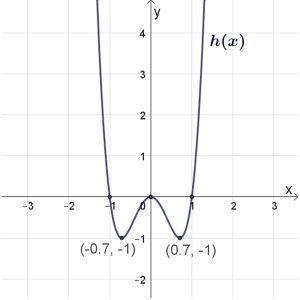
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-1,0)\)
נקודות קיצון: מינימום \((0.7,-1)\) , \((-0.7,-1)\) מקסימום \((0,0)\)
- סרטטו באותה מערכת צירים, בצבעים שונים, את הגרפים של:
א. \(h^3(x)\)
ב. \(h^2(x)\) - באיזה תחום \(h^3(x)\gt{h^2(x)}\)? (דייקו בתשובתכם ככל האפשר).
- לאיזו פונקציה מבין הפונקציות \(h^3(x)\) , \(h^2(x)\), \(h(x)\) יש נקודות פיתול בהן שיפוע המשיק הוא אפס?
מה הם שיעורי נקודות אלה?
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) ולפחות שבע נקודות צהובות (לסרטוט \(f^3(x)\)), במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- כדי "לנקות" את היישומון ולהתחיל מחדש עם הפונקציה המוצגת, ניתן ללחוץ על אתחול.
\(g(x)\)
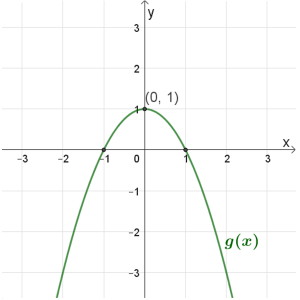
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,1)\) , \((-1,0)\)
נקודת קיצון: מקסימום \((0,1)\)
- סרטטו באותה מערכת צירים, בצבעים שונים, את הגרפים של:
א. \(g^3(x)\)
ב. \(g^2(x)\) - באיזה תחום \(g^3(x)\gt{g(x)}\)? (דייקו בתשובתכם ככל האפשר).
- לאיזו פונקציה מבין הפונקציות \(g^3(x)\) , \(g^2(x)\), \(g(x)\) יש נקודות פיתול בהן שיפוע המשיק הוא אפס?
מה הם שיעורי נקודות אלה?
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) ולפחות שבע נקודות צהובות (לסרטוט \(f^3(x)\)), במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- כדי "לנקות" את היישומון ולהתחיל מחדש עם הפונקציה המוצגת, ניתן ללחוץ על אתחול.
\(p(x)\)
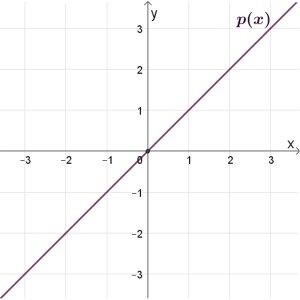
נקודת חיתוך עם הצירים: \((0,0)\)
- סרטטו באותה מערכת צירים, בצבעים שונים, את הגרפים של:
א. \(p^3(x)\)
ב. \(p^2(x)\) - באיזה תחום \(p^3(x)\ge{p^2(x)}\)? (דייקו בתשובתכם ככל האפשר).
- לאיזו פונקציה מבין הפונקציות \(p^3(x)\) , \(p^2(x)\), \(p(x)\) יש נקודות פיתול בהן שיפוע המשיק הוא אפס?
מה הם שיעורי נקודות אלה?
תוכלו לבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות כחולות (לסרטוט \(f^2(x)\)) ולפחות שבע נקודות צהובות (לסרטוט \(f^3(x)\)), במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מכל אחד מהצבעים.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- כדי "לנקות" את היישומון ולהתחיל מחדש עם הפונקציה המוצגת, ניתן ללחוץ על אתחול.





















