חזקה טבעית של פונקציה - חלק ד' - \(f^n{(x)}\) - למורה
חומר לימוד:
המשותף והשונה בין הפונקציות \(f^n(x)\) עבור \(n\) זוגי ועבור \(n\) אי זוגי. שילובים בין חזקה טבעית של פונקציה, הזזות ומתיחות של פונקציה וערך מוחלט של פונקציה.
ליישום והעמקה בנושא חזקה טבעית של פונקציה (ראו משימות: "חזקה שניה של פונקציה", ו"חזקה שלישית של פונקציה")
כיתה:
כיתה י'
מבנה המשימה:
בעיית מטרה אחת, שלה שתי מדרגות.
ידע קודם:
- הכרת הגרף של \(f^2(x)\) ושל \(f^3(x)\) כאשר נתון הגרף של \(f(x)\) [\(f(x)\) פולינום].
- ערך מוחלט של פונקציה.
- הזזות ומתיחות של פונקציה.
- משימה זו מקומה לאחר המשימות: "חזקה שניה של פונקציה", ו"חזקה שלישית של פונקציה".
מטרות לימודיות:
המשותף והשונה בין:
- \(f^2(x)\) , ו- \(f^4(x)\)
- \(f^5(x)\) , ו- \(f^3(x)\)
- \(f^2(x)\) , ו- \(|f(x)|\)
משימת המטרה:
בבעיית המטרה נתון גרף של פונקציה שלה שלוש נקודות קיצון, וערך המקסימום המוחלט הוא \(1\).
מדרגה 1:
נתון גרף של פרבולה בעלת מינימום, כשערך המינימום הוא \(-2\).
מדרגה 2:
נתון גרף של פרבולה בעלת מקסימום וערך המקסימום הוא \(1\).
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה.
שיעורי בית:
סיום המשימה.
משימות מומלצות:
\(f(x)\)
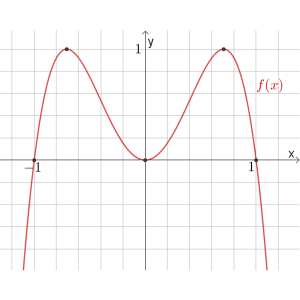
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-1,0)\)
נקודות קיצון: מקסימום \((0.75,1)\) , \((-0.75,1)\) , מינימום \((0,0)\)
נתונים 4 זוגות של פונקציות:
\(f(x)\) , \(0.5f(x)\)
\(|f(x)|\) , \(f^2(x)\)
\(f^5(x)\) , \(f^3(x)\)
\(f^4(x)\) , \(f^2(x)\)
ובטבלה הבאה נתונים 6 זוגות של גרפים:
א
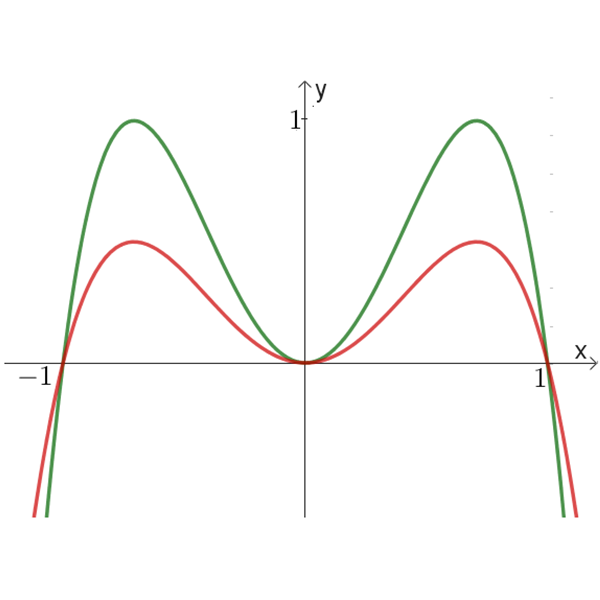
ב
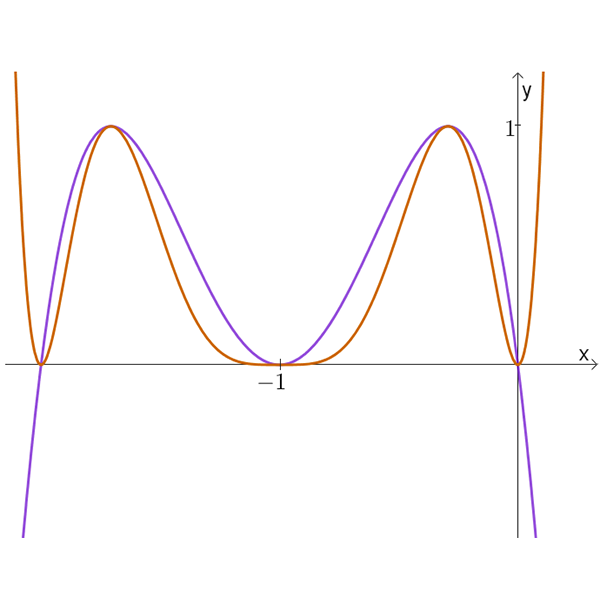
ג
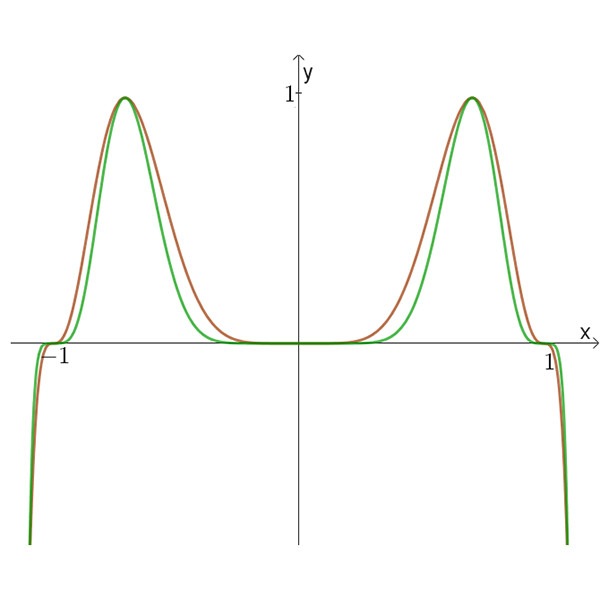
ד
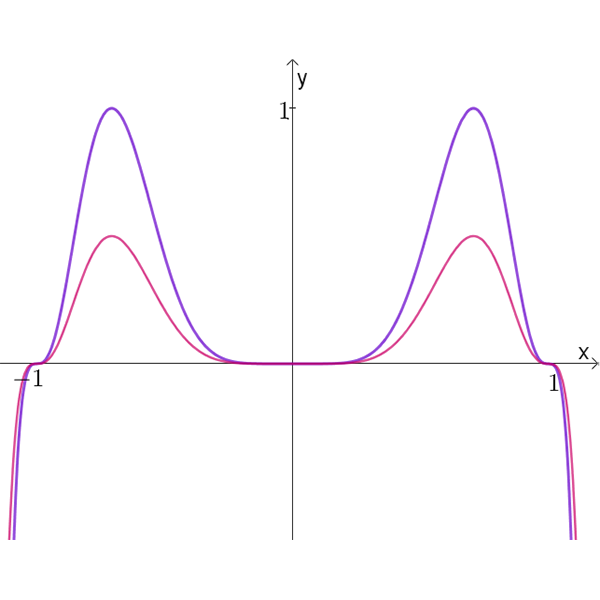
ה
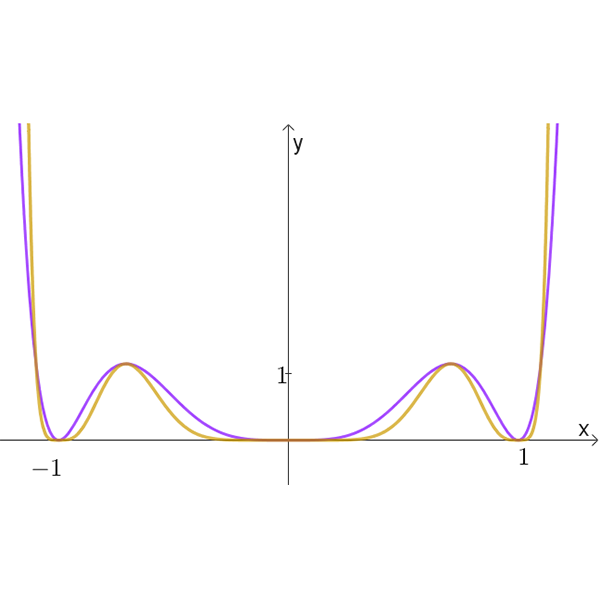
ו
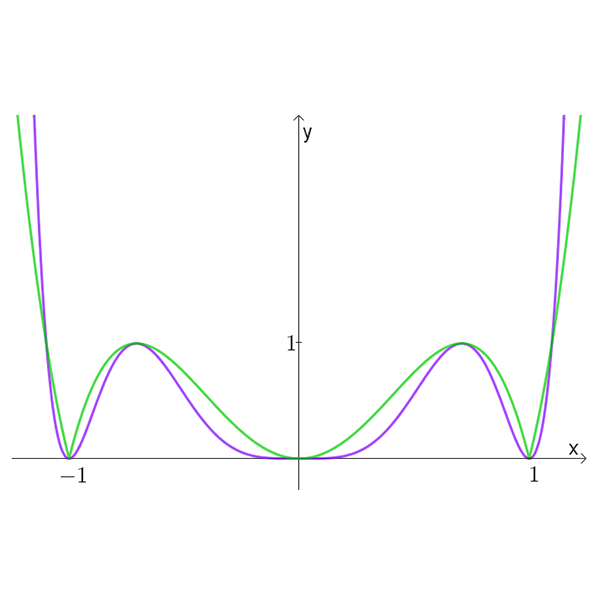
- לזוגות הגרפים בטבלה הנתונה, התאימו זוג מפונקציות מהרשימה הנתונה למעלה.
כמו כן, התאימו לכל אחד מהגרפים שבתוך כל זוג את הפונקציה המתאימה לו. נמקו תשובתכם. - לשני זוגות הגרפים שלא נמצאה להם התאמה מבין זוגות הפונקציות הנתונות, מצאו בעצמכם איזו פונקציה יכולה להתאים לכל אחד מהגרפים האלה.
- במידת הצורך פתרו את הבעיות במדרגה 1.
פתרונות לבעיית מטרה:
זוג גרפים א
זוג גרפים ב
(חסרה התאמה)
זוג גרפים ג
זוג גרפים ד
(חסרה התאמה)
הצעה אפשרית:
זוג גרפים ה
זוג גרפים ו
\(f(x)\)
ירוק
\(f{(x+1)}\)
סגול
\(f^3(x)\)
חום
\(f^3(x)\)
ורוד
\(f^2(x)\)
סגול
\(f^2(x)\)
סגול
\(0.5{f(x)}\)
אדום
\(f^2{(x+1)}\)
כתום
\(f^5(x)\)
ירוק
\(2\cdot{f^3(x)}\)
סגול
\(f^4(x)\)
חום
\(|f(x)|\)
ירוק
\(g(x)\)
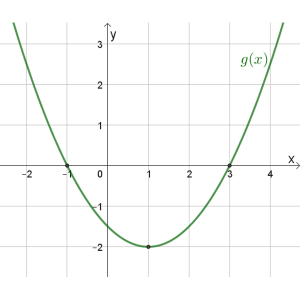
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((3,0)\) , \((0,-1.5)\) , \((-1,0)\)
נקודת מינימום: \((1,-2)\)
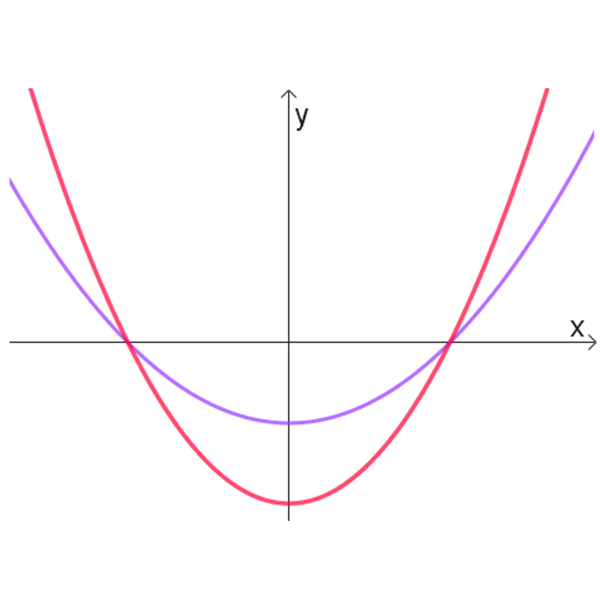
לפניכם רשימה של 3 זוגות של פונקציות:
\(g(x)\) , \(2{g(x)}\)
\(|g(x)|\) , \(g^2(x)\)
\(g(x)\) , \(g^3(x)\)
ובטבלה הבאה נתונים 6 זוגות של גרפים:
א
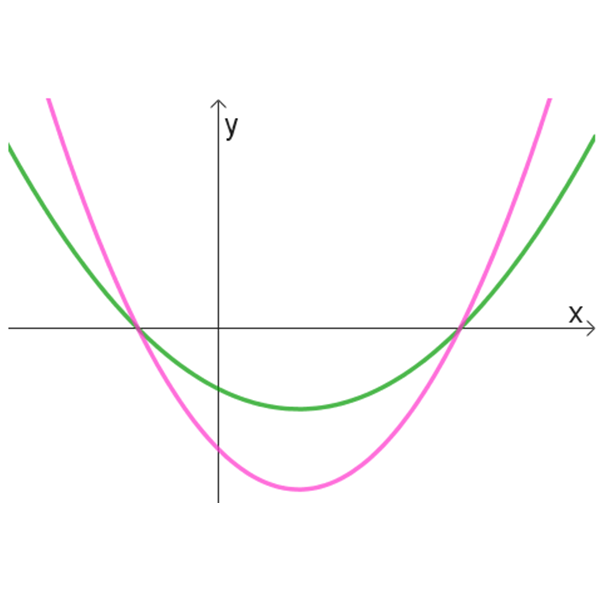
ב
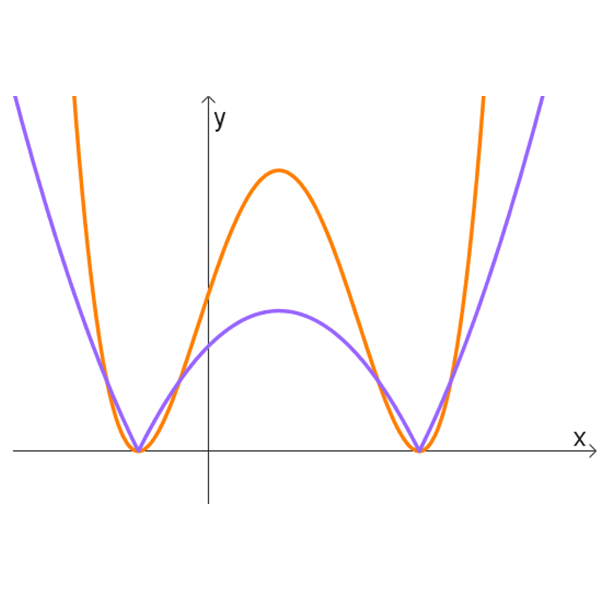
ג
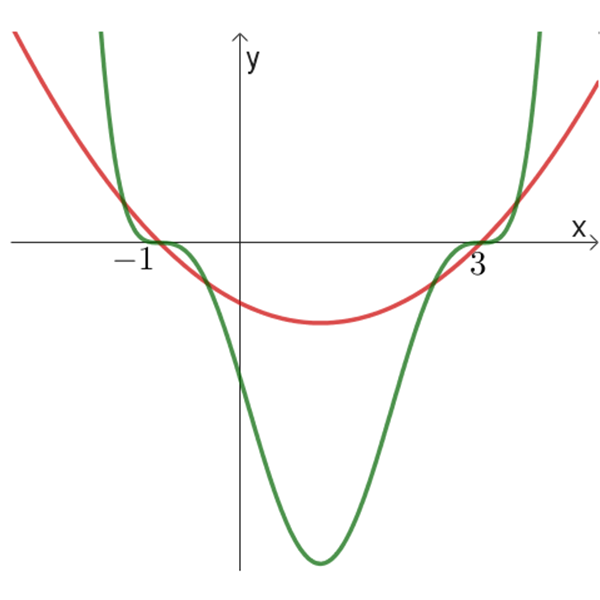
ד
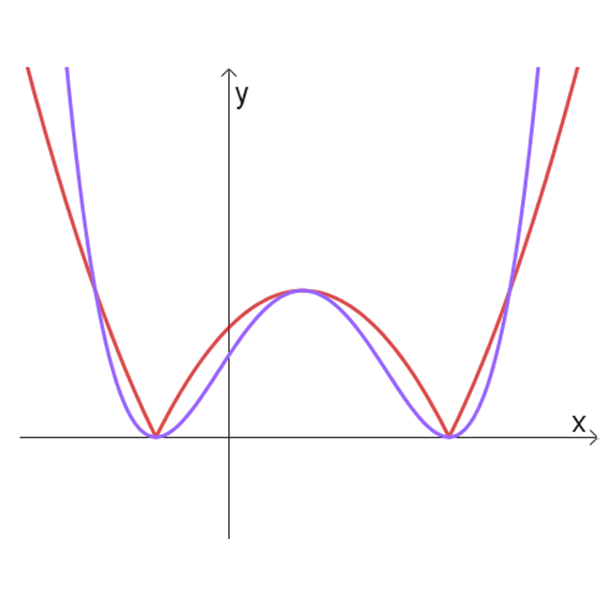
ה
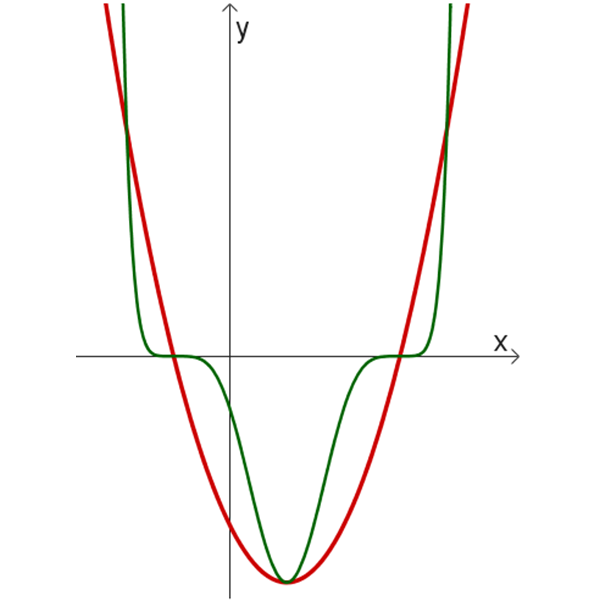
ו
- לזוגות הגרפים בטבלה הנתונה, התאימו זוג פונקציות מהרשימה הנתונה למעלה.
כמו כן, התאימו לכל אחד מהגרפים שבתוך כל זוג את הפונקציה המתאימה לו. נמקו תשובתכם. - לשלושה זוגות הגרפים שלא נמצאה להם התאמה מבין זוגות הפונקציות הנתונות, מצאו בעצמכם איזו פונקציה יכולה להתאים לכל אחד מהגרפים האלה.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
\(h(x)\)
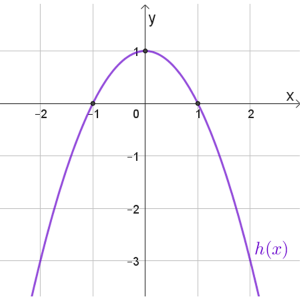
תחום הגדרה: כל \(x\)
נקודות החיתוך עם הצירים: \((1,0)\) , \((0,1)\) , \((-1,0)\)
נקודות מקסימום: \((0,1)\)
לפניכם רשימה של 3 זוגות של פונקציות:
\(h^2(x)\) , \(2{h^2(x)}\)
\(|h(x)|\) , \(h^2(x)\)
\(h^5(x)\) , \(h^3(x)\)
ובטבלה הבאה נתונים 6 זוגות של גרפים:
א
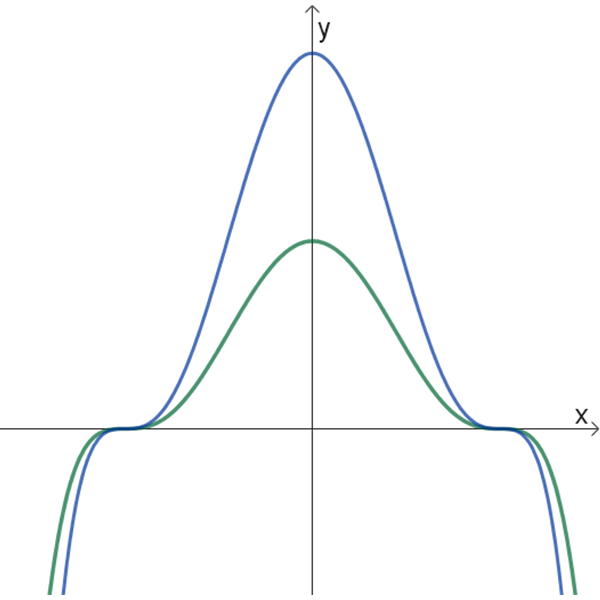
ב
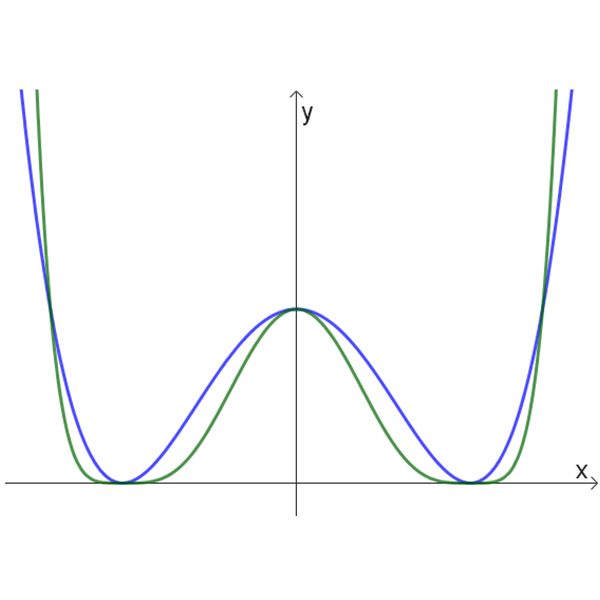
ג
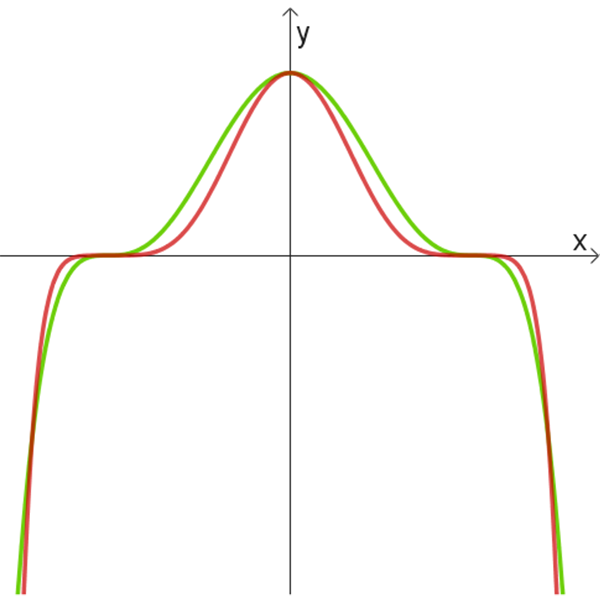
ד
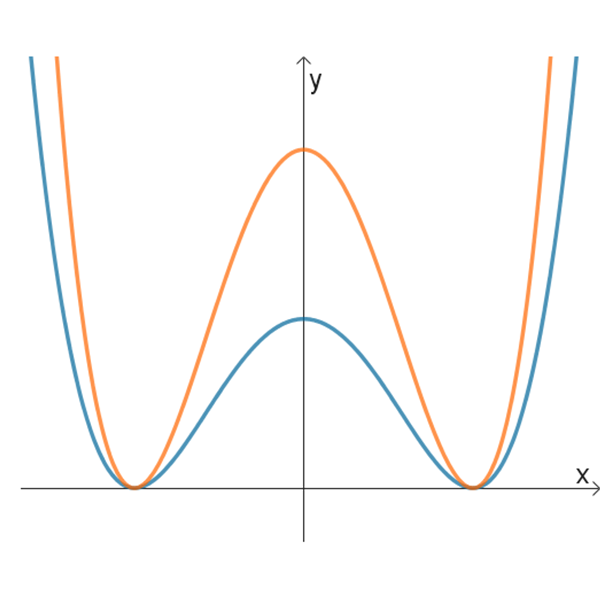
ה
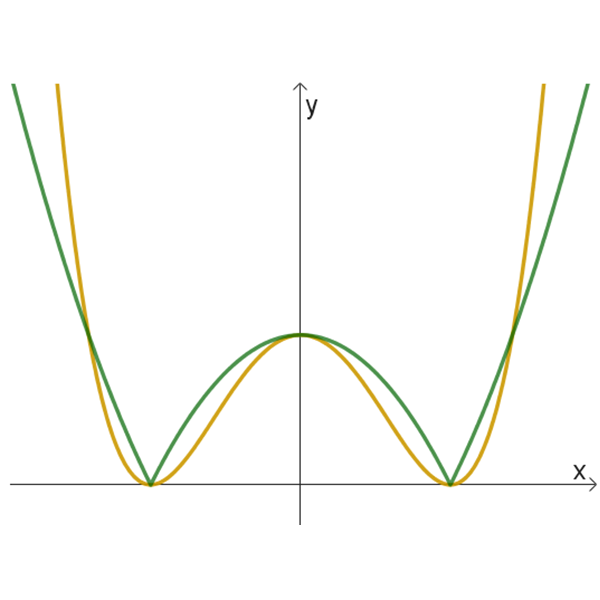
ו
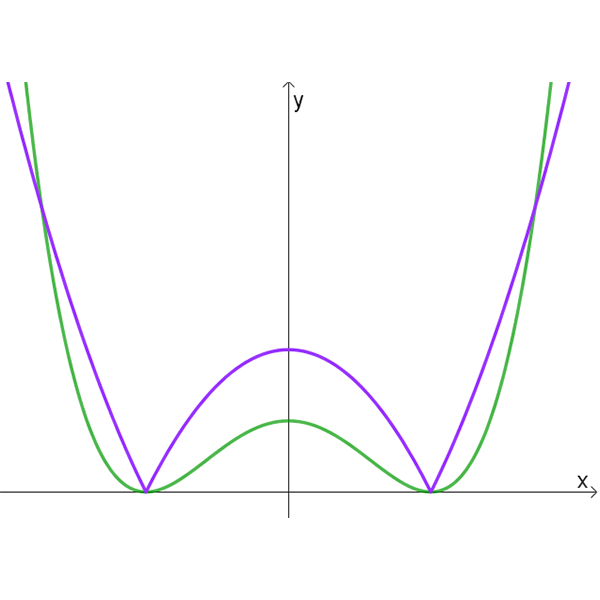
- לזוגות הגרפים בטבלה הנתונה, התאימו זוג פונקציות מהרשימה הנתונה למעלה.
כמו כן, התאימו לכל אחד מהגרפים שבתוך כל זוג את הפונקציה המתאימה לו. נמקו תשובתכם. - לשלושה זוגות הגרפים שלא נמצאה להם התאמה מבין זוגות הפונקציות הנתונות, מצאו בעצמכם איזו פונקציה יכולה להתאים לכל אחד מהגרפים האלה.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.





















