חזקה טבעית של פונקציה - חלק ב' - חזקה שלישית \(f^3{(x)}\) - למורה
חומר לימוד:
סרטוט הגרף של הפונקציה \(f^3(x)\), כאשר נתון הגרף של הפונקציה \(f(x)\), עבור \(f(x)\) פולינום. התחלת הוראת הנושא. רצוי לתת משימה זו לאחר המשימה "חזקה טבעית של פונקציה – חלק א – חזקה שניה".
כיתה:
כיתה י'
מבנה המשימה:
בעיית מטרה ושלוש בעיות מדרגה. לכל אחת מהבעיות מצורפים יישומונים.
ידע קודם:
- הכרת הפונקציות \(x^n\) (עבור \(n\) טבעי)
תכונות של פונקציה כמו:
- נקודות חיתוך עם הצירים
- נקודות קיצון וסוגן
- תחומי עליה וירידה
- תחומי חיוביות ושליליות
- קצב שינוי של פונקציה
- נקודות פיתול
- נקודות חיתוך בין פונקציות
מטרות לימודיות:
- אפיון קשרים בין גרף של פונקציית פולינום \(f(x)\) לבין גרף הפונקציה \(f^3(x)\), בלי הכרח להיעזר בנגזרת.
- נקודות הפיתול של הפונקציה \(f^3(x)\) בנקודות האפס, בהן שיפוע המשיק אפס (בהקבלה למעבר מ- \(x\) ל- \(x^3\)).
- נקודות חיתוך בין הפונקציות \(f(x)\) ו- \(f^3(x)\) והמצב ההדדי ביניהן.
סוג הדירוג:
שלוש מדרגות: בכל מדרגה יש לסרטט את הגרף של \(f^3(x)\) כאשר הגרף הנתון של \(f(x)\) מכיל פחות נקודות קיצון ו/או נקודות חיתוך עם ה-\(x\) ביחס למדרגה הקודמת.
משימת המטרה:
פולינום ולו שתי נקודות חיתוך עם ציר ה-\(x\) ונקודת השקה אחת ושלוש נקודות קיצון.
מדרגה 1:
פולינום ולו שתי נקודות חיתוך עם ציר ה-\(x\), ושתי נקודות קיצון.
מדרגה 2:
פרבולה קעורה סימטרית לציר ה-\(y\). נקודת המינימום שלה היא \((0,-1.5)\).
מדרגה 3:
שתי פונקציות, האחת קו ישר והשניה פרבולה שנקודת המינימום שלה היא \((0,0)\).
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. רצוי להיעזר ביישומונים המצורפים.
בדיון בכיתה רצוי לדון בנקודות הבאות:
- אם \(0<a<b\), מה הסדר בין הגדלים של \(a^3\) ו- \(b^3\)?
ואם \(a<b<0\), מה הסדר בין הגדלים של \(a^3\) ו- \(b^3\)?
(ניתן להיעזר בדוגמאות מספריות) - כיצד תכונות אלה של מספרים קשורות לתחומי עליה וירידה של \(f^3(x)\) ולנקודות הקיצון?
- אם \(f(x)=0\) אז \(f^3(x)=?\)
אם \(f(x)=1\) אז \(f^3(x)=?\)
אם \(f(x)=-1\) אז \(f^3(x)=?\)
לפיכך, אילו נקודות יכולות להיות נקודות משותפות ל- \(f(x)\) ול \(f^3(x)\)? - כאשר מעלים בשלישית מספר בין \(0\) ל- \(1\), האם התוצאה גדלה או קטנה?
(ניתן להיעזר בדוגמאות מספריות). - כאשר מעלים בשלישית מספר הגדול מ- \(1\), האם התוצאה גדלה או קטנה?
- כאשר מעלים בשלישית מספר בין \(-1\) ל- \(0\), האם התוצאה גדלה או קטנה?
- כאשר מעלים בשלישית מספר הקטן מ- \(-1\), האם התוצאה גדלה או קטנה?
- אם כך מה ניתן להסיק?
- עבור אילו ערכי \(f(x)\) מתקיים ש: \(f(x)<f^3(x)\)?
עבור אילו ערכי \(f(x)\) מתקיים ש: \(f(x)>f^3(x)\)? - מדוע בנקודות החיתוך של \(f(x)\) עם ציר ה- \(x\) יש ל- \(f^3(x)\) נקודות פיתול? (מה קורה לקצב השינוי של הפונקציה?)
שימוש ביישומונים:
בכל בעיה ובכל שלב השימוש ביישומונים הוא לצורך בדיקה, לאחר שתלמיד חשב על השאלה והגיע למסקנות הנידרשות. אם תלמיד טעה / או לא ידע, שימוש ביישומונים יכול לעזור לו, אבל חשוב שתלמיד יידע לנמק את תשובותיו לאחר שנעזר ביישומון.
שיעורי בית:
סיום המשימה. ניתן לעבור למשימות נוספות בנושא זה.
משימות מומלצות:
משימה מקדימה:
משימות המשך למשימה זו:
\(f(x)\)
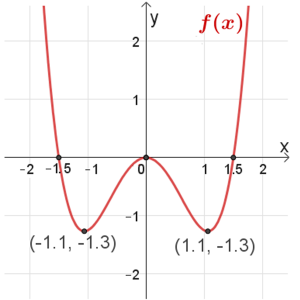
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1.5,0)\) , \((-1.5,0)\)
נקודות קיצון: מינימום \((1.1,-1.3)\) , \((-1.1,-1.3)\), מקסימום \((0,0)\)
שימו לב גם לנקודות החיתוך בין \(f(x)\) ל-\(f^3(x)\) ולמצב ההדדי ביניהן.
שימו לב להתנהגות הפונקציה \(f^3(x)\) בסביבת נקודות החיתוך שלה עם ציר ה-\(x\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
סעיף ב
\(f(x)\)היא פונקציית פולינום כלשהו.
אילו קשרים מצאתם שקיימים בין גרף הפונקציה \(f(x)\) לבין גרף הפונקציה \(f^3(x)\)? נמקו תשובתכם.
תוכלו לבדוק קשרים בין \(f(x)\) ל-\(f^3(x)\) עבור פונקציות נוספות בעזרת היישומונים הדינאמיים המצורפים.
- במידת הצורך פתרו את הבעיות במדרגה 1.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
 ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ  בתפריט העליון.
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
 שבפינה הימנית העליונה.
שבפינה הימנית העליונה.
- ניתן להזיז את הפולינום הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן לשנות את הגרף הנתון על-ידי: שינוי הפרמטרים \(k\) , \(d\) , \(n\) בעזרת סרגלי הגרירה. (נסו תחילה להבין מהי המשמעות של כל אחד מהפרמטרים)
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה האדומה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.
\(h(x)\)
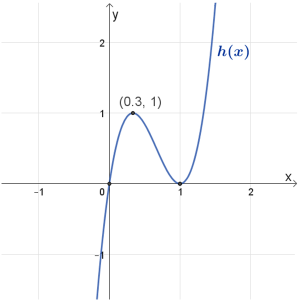
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\)
נקודות קיצון: מקסימום \((0.3,1)\), מינימום \((1,0)\)
שימו לב גם לנקודות החיתוך בין \(h(x)\) ל-\(h^3(x)\) ולמצב ההדדי ביניהן.
שימו לב להתנהגות הפונקציה \(h^3(x)\) בסביבת נקודות החיתוך שלה עם ציר ה-\(x\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
 ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ  בתפריט העליון.
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
 שבפינה הימנית העליונה.
שבפינה הימנית העליונה.
\(t(x)\)
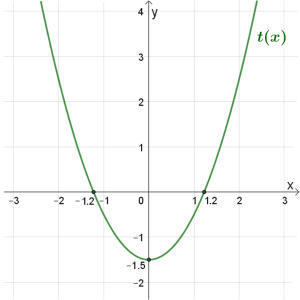
תחום הגדרה: כל \(x\)
נקודות חיתוך עם הצירים: \((1.2,0)\) , \((-1.2,0)\)
נקודת קיצון: מינימום \((0,-1.5)\)
שימו לב גם לנקודות החיתוך בין \(t(x)\) ל-\(t^3(x)\) ולמצב ההדדי ביניהן.
שימו לב להתנהגות הפונקציה \(t^3(x)\) בסביבת נקודות החיתוך שלה עם ציר ה- \(x\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
 ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ  בתפריט העליון.
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
 שבפינה הימנית העליונה.
שבפינה הימנית העליונה.
\(g(x)\)
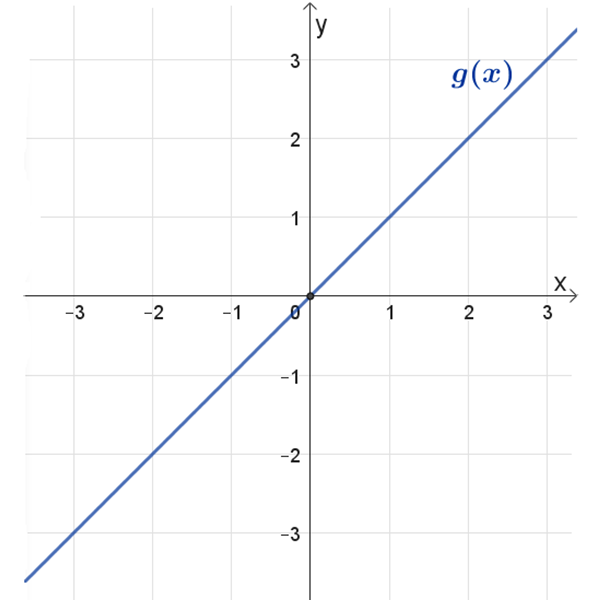
\(p(x)\)
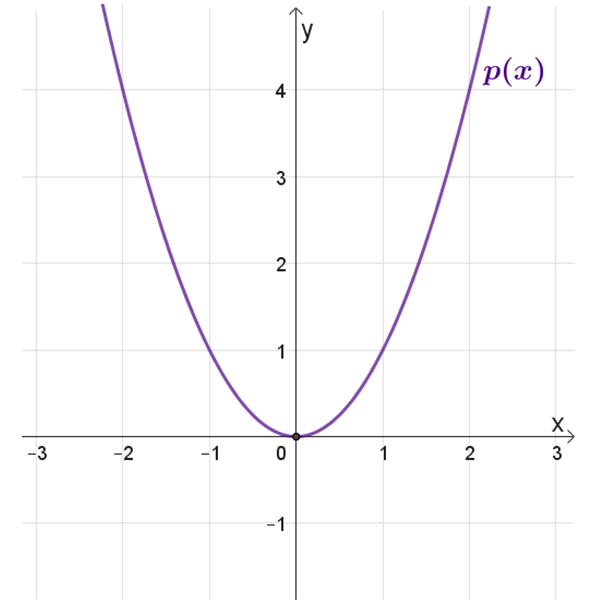
נקודת חיתוך עם הצירים: \((0,0)\)
תחום הגדרה: כל \(x\)
נקודת חיתוך עם הצירים: \((0,0)\)
נקודת קיצון: מינימום \((0,0)\)
שימו לב, בכל אחד מהסעיפים, גם לנקודות החיתוך בין הגרפים ולמצב ההדדי ביניהם.
שימו לב להתנהגות הפונקציות, בכל אחד מהסעיפים, בסביבת נקודות החיתוך שלהן עם ציר ה- \(x\).
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות במקומות המתאימים להן.
- יש להיעזר בעיפרון
 שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות.
- במידת הצורך, ניתן להציג שיקוף של הנקודה האדומה על ידי בחירה של האפשרות המתאימה בתפריט שבתחתית היישומון: שיקוף בציר ה-\(x\) או בציר ה-\(y\).
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
 ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ  בתפריט העליון.
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
 שבפינה הימנית העליונה.
שבפינה הימנית העליונה.





















