זווית בין שני מישורים - למורה
חומר לימוד:
זיהוי זווית בין שני מישורים, חישוב זווית ביו שני מישורים בדרכים שונות: בעזרת טריגונומטריה במרחב ובעזרת ווקטורים. המשימה מתאימה לתרגול ויישום הנלמד בטריגונומטריה במרחב ובווקטורים.
כיתה:
כיתה י"ב
מבנה המשימה:
בעיית מטרה ושלוש מדרגות. בסוף המשימה ישנה שאלת אתגר. לכל המדרגות יש יישומונים.
ידע קודם:
- הגדרת זווית בין שני מישורים
- משפט שלושת האנכים
- תכונות תיבה
- משוואה כללית של מישור
- חישוב זווית בין מישורים בעזרת ווקטורים
- לשאלת האתגר: פירמידה מרובעת ישרה
מטרות לימודיות:
- פיתוח ראיה מרחבית
- פיתוח היכולת לזהות זווית בין מישורים בעזרת משפט שלושת האנכים
- קישור בין הנושאים: טריגונומטריה במרחב וווקטורים
משימת המטרה:
שתי בעיות: בקובייה – יש לזהות ולחשב את הזווית שנבנית באופן זהה לזווית אשר בבעיית המטרה, בתיבה – יש לזהות ולחשב זווית בין מישור בתוך התיבה לבין פאת הבסיס של התיבה.
מדרגה 1:
שתי בעיות: בקובייה – יש לזהות ולחשב את הזווית שנבנית באופן זהה לזווית אשר בבעיית המטרה, בתיבה – יש לזהות ולחשב זווית בין מישור בתוך התיבה לבין פאת הבסיס של התיבה.
מדרגה 2:
שתי בעיות אחת בקובייה והשנייה בתיבה. בקובייה יש לזהות ולחשב זווית בין מישור בתוך הקובייה לבין פאת הבסיס. בתיבה השאלה היא מספרית ומכילה הדרכה לגבי זיהוי זווית בין מישורים שעשוי לעזור בפתרון בעיית המטרה.
מדרגה 3:
בעיה מספרית בתיבה, ובה הדרכה מפורטת שמובילה לזיהוי זווית בין מישורים שעשוי לעזור בפתרון בעיית המטרה.
בעיית אתגר:
אין חובה לפתור את בעיית האתגר (פירמידה).
שיטת הוראה:
בכיתה:
תלמידים יקבלו את כרטיס המטרה, במידת הצורך יעברו למדרגות השונות, על-פי בחירתם, או על-פי הנחיה מהמורה.
רצוי לקיים דיון כיתתי במהלך השיעור ביחס לזיהוי הזווית הנדרשת בבעיית המטרה. קיים יישומון למורה בו ניתן להיעזר בדיון.
יש לציין כי מציאת הזווית בין מישורים בתיבה, ללא משפט שלושת האנכים, יכולה למעשה להוביל להוכחת המשפט.
שימוש ביישומונים:
ישנם יישומונים בכל אחת מהמדרגות.
שיעורי בית:
סיום המשימה.
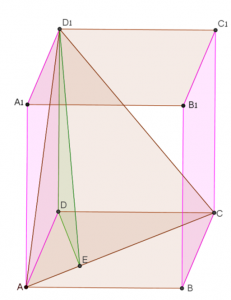
- זהו את הזווית בין מישור \(ACD_1\) לבין מישור \(ADD_1 A_1\). נמקו תשובתכם.
- נתונים נוספים: \(AB=a=7k\) , \(BC=b=6k\) , \(AA_1=c=10k\).
חשבו את הזווית בין מישור \(ACD_1\) לבין מישור \(ADD_1 A_1\) בדרכים שונות.
- בסיום תוכלו לעבור לבעיית האתגר.
- במידת הצורך פתרו את הבעיות במדרגה 1.
הערה: יישומון זה הינו חלק מהמדריך למורה, ולא מוצג לתלמידים
פתרונות לבעיית המטרה
- בניה: \(MD\) מאונך ל-\(AD_1\).
יש להוכיח כי \(MC\) מאונך ל- \(AD_1\) (זאת ניתן להוכיח בעזרת משפט שלושת האנכים):\(CM\) – משופע, \(CD\) – אנך למישור \(ADD_1A_1\) , לכן \(MD\) היטלו של המשופע על המישור.
\(AD_1\) הוא ישר במישור \(ADD_1 A_1\) המאונך להיטלו של משופע \((DM)\) על המישור – מאונך גם למשופע \((MC)\), ולכן \(AD_1\) מאונך ל- \(MC\). (ניתן להוכיח גם בדרכים אחרות… )
הזווית בין שני המישורים היא זווית \(DMC\).
- הזווית שווה ל: \(53.68^{\circ}\)
דרך נוספת: בעזרת ווקטורים.
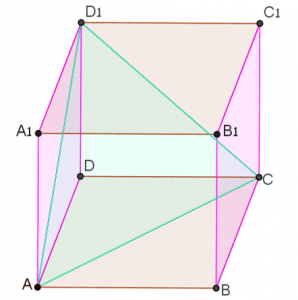
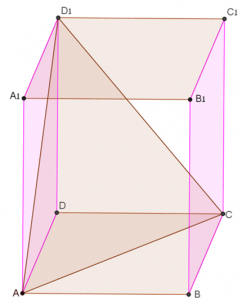
זהו את הזווית בין מישור \(ACD_1\) לבין מישור \(ADD_1 A_1\). נמקו תשובתכם בשתי דרכים שונות.
ניתן להיעזר ביישומון המצורף.
סעיף ב
נתונה תיבה \(ABCDA_1B_1C_1D_1\) , \(AB=a\) , \(BC=b\) , \(AA_1=c\).
- זהו את הזווית בין מישור \(ACD_1\) לבין מישור \(ABCD\). נמקו תשובתכם.
- השוו בין תהליך זיהוי הזווית בין שני המישורים של הבעיה הראשונה (סעיף א), לבין זיהוי הזווית בין שני המישורים בבעיה השנייה (סעיף ב) – במה התהליכים דומים ובמה הם שונים.
ניתן להיעזר ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש להיעזר בחיצי האתחול
שבחלק התחתון של היישומון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש להיעזר בחיצי האתחול שבחלק התחתון של היישומון.
זהו את הזווית בין מישור \(ACD_1\) לבין מישור \(ABCD\).
סעיף ב
נתונה תיבה \(ABCDA_1B_1C_1D_1\) , \(AB=7\space{cm}\) , \(BC=6\space{cm}\) , \(AA_1=10\space{cm}\).
\(DE\) אנך ל- \(AC\).
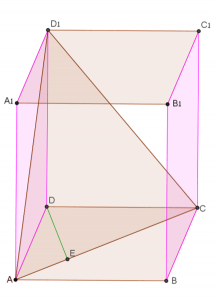
- זהו את הזווית בין מישור \(ACD_1\) לבין מישור \(ABCD\).
- חשבו את הזווית בין מישור \(ACD_1\) לבין מישור \(ABCD\) בדרכים שונות.
ניתן להיעזר ביישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש להיעזר בחיצי האתחול שבחלק התחתון של היישומון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש להיעזר בחיצי האתחול שבחלק התחתון של היישומון.
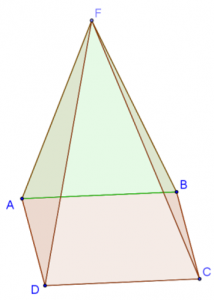
פתרון בעיית האתגר
הזווית בין המישורים היא בת \(84.85^{\circ}\) – בוחרים את הזווית החדה.
הזווית בין פאות הפירמידה היא בת \(95.15^{\circ}\).
אפשר לפתור כך:
- חישוב גובה ל-\(AF\) בפאה \(AFB\).
- חישוב גובה ל-\(AF\) בפאה \(AFD\).
- משפט הקוסינוסים במשולש שצלעותיו הם שני הגבהים ואלכסון המלבן שהוא בסיס הפירמידה.