מנת חזקות של בינומים – כיצד זה נראה? - למורה
חומר לימוד:
חקירה של משפחת הפונקציות הרציונאליות: \(f{(x)}=\Large\frac{(x-a)^n}{(x-b)^m}\) , \(a \ne b\) , m , n טבעיים גדולים מ- 1.
חקירת המשפחה מזמנת פיתוח הבנה של הקשר בין הריבוי של השורש במונה ובמכנה לבין התנהגות הגרף בסביבת הנקודות הרלוונטיות. ממשפחה זו ניתן לעבור לפונקציות אחרות ולהיווכח שהמסקנות נכונות גם עבורן.
כיתה:
כיתה י"א
מבנה המשימה:
בעיית מטרה ושתי בעיות מדרגה, להן יש יישומון.
ידע קודם:
- זיהוי אסימפטוטות אנכיות ואופקיות
- תחומי חיוביות ושליליות של פונקציה
- מיומנויות חקירה של פונקציה
- נגזרת של מנה ופונקציות מורכבות
מטרות לימודיות:
- בחינת ההשפעה של הריבוי של השורש במונה על צורת המפגש/חיתוך עם ציר ה- x.
- בחינת ההשפעה של הריבוי של השורש במכנה על ההתנהגות משני צידי אסימפטוטה אנכית.
- בחינת ההתנהגות של הגרף ב"אינסופים" – אסימפטוטה אופקית או לא. אפשר להתייחס לעקום אסימפטוטי. במשפחה זו: \(f(x)=x^n\), \(n\) טבעי.
- טכניקה אלגברית של גזירת מנה בשילוב פונקציה מורכבת בדגש על זיהוי גורמים משותפים והוצאתם מחוץ לסוגריים, לצורך מציאת איפוסי נגזרת.
משימת המטרה:
שני חלקים. בחלק א', נתונה טבלה ובה בכל שורה שלוש פונקציות ושני גרפים. יש להתאים בין הפונקציות לגרפים ולהציע סקיצה של גרף לפונקציה השלישית.
בחלק ב', יש לאפיין את הפונקציות במשפחה בהתאם לערכי הפרמטרים.
מדרגה 1:
נתונות: רשימה של פונקציות ורשימה של תכונות. יש למיין את הפונקציות לפי התכונות הנתונות.
מדרגה 2:
נתונות חמש פונקציות וחמישה גרפים. יש להתאים בין הפונקציות לגרפים, כאשר התלמיד מכוון לשים לב להתנהגות הפונקציות בסביבת האסימפטוטות ובסביבת נקודת החיתוך עם ציר ה-\(x\).
שיטת הוראה:
בכיתה:
עבודה בזוגות או בקבוצות. מתחילים מבעיית המטרה. בשתי המדרגות מגיעים לחקירה מלאה של המשפחה המופיעה בבעיית המטרה.
בדיון מסכם במליאה מומלץ לבקש לשער השערה ביחס לגרפים של פונקציות "מסובכות" יותר, על ידי הכללה של המסקנות.
למשל: \(g(x)=\Large\frac{(2-x)^3}{(x-3)^4}\) , \(h(x)=\Large\frac{(2-x)^3(x-1)^2}{(x+1)^4}\) , \(k(x)=\Large\frac{x^3(x-1)^2}{(x+1)^4(x-2)^3}\)
שימוש ביישומונים:
יש יישומונים במדרגות 1 ו-2.
שיעורי בית:
סיום המשימה.
הערה:
ניתן לבצע את המשימה ללא טכניקה של גזירה וללא מציאת נקודות קיצון.
בעיית מטרה
לפניכם גרפים של פונקציות ורשימה של פונקציות מהמשפחה: \(f{(x)}=\Large\frac{(x-a)^n}{(x-b)^m}\) , \(a \ne b\) , m , n טבעיים גדולים מ- 1.
חלק א:
בכל שורה שני גרפים ושלוש פונקציות.
התאימו בין הגרפים לפונקציות והציעו סקיצה לפונקציה שאין לה גרף בשורה.
נמקו את תשובותיכם.
חלק ב:
אפיינו את הפונקציות במשפחה בהתאם לערכים של הפרמטרים.
תנו דעתכם על היחס בין a ל-b (מי גדול ממי, או שווה), הזוגיות של m ,n, והיחס ביניהם, והשפעה של אלה על תכונות הפונקציות.
א
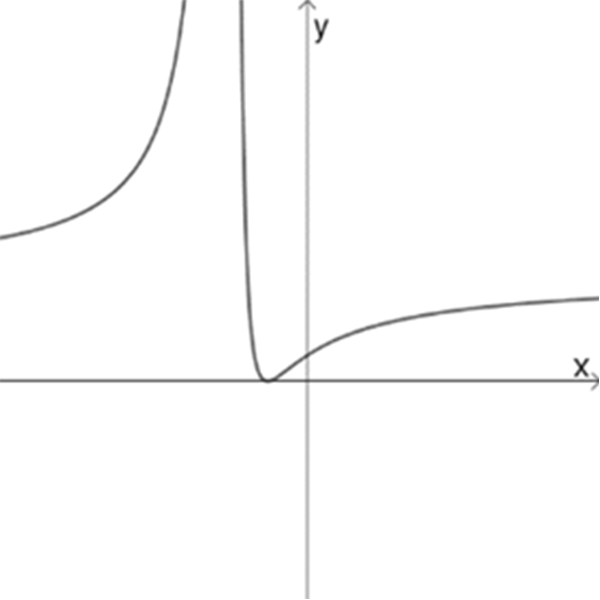
ב
\(f_{1}(x)=\Large\frac{(x-2)^3}{(x-3)^2}\)
\(f_{2}(x)=\Large\frac{x^4}{(x-1)^4}\)
\(f_{3}(x)=\Large\frac{(x+1)^2}{(x+3)^2}\)
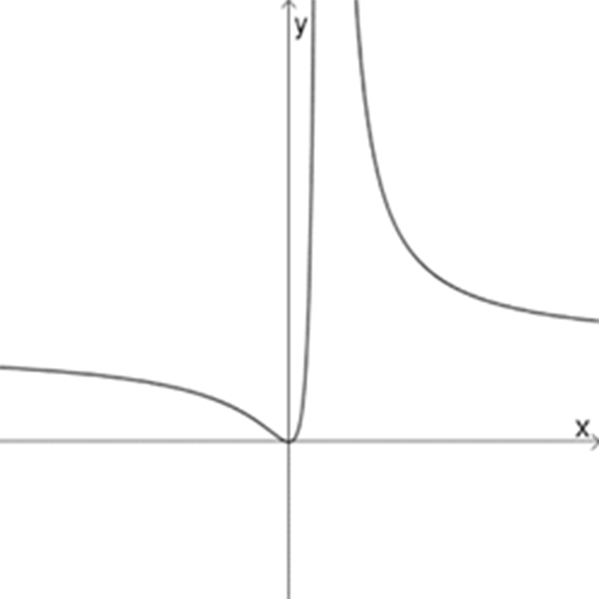
ג
ד

\(f_{4}(x)=\Large\frac{(x+1)^2}{(x+2)^2}\)
\(f_{5}(x)=\Large\frac{(x+3)^2}{(x+2)^4}\)
\(f_{6}(x)=\Large\frac{(x+1)^2}{(x+2)^3}\)
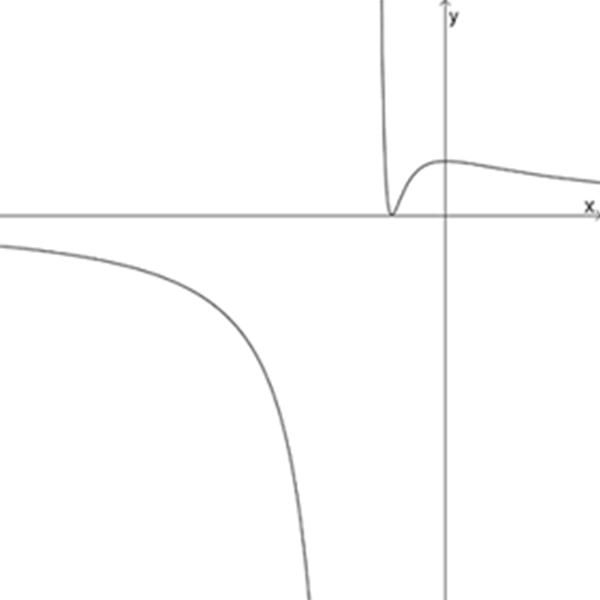
ה
ו
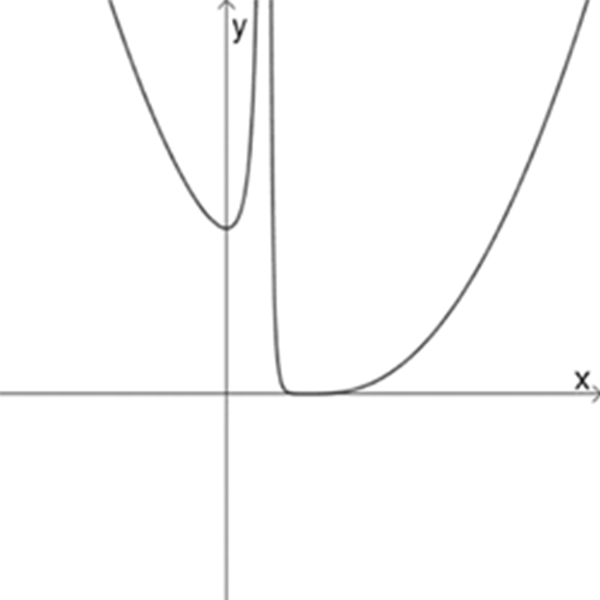
\(f_{7}(x)=\Large\frac{(x+1)^3}{(x+2)^2}\)
\(f_{8}(x)=\Large\frac{x^2}{(x-1)^2}\)
\(f_{9}(x)=\Large\frac{(x-2)^4}{(x-1)^2}\)
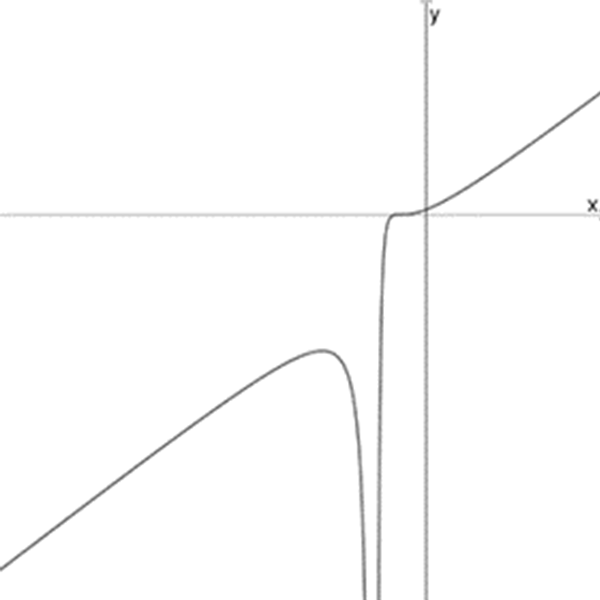
ז
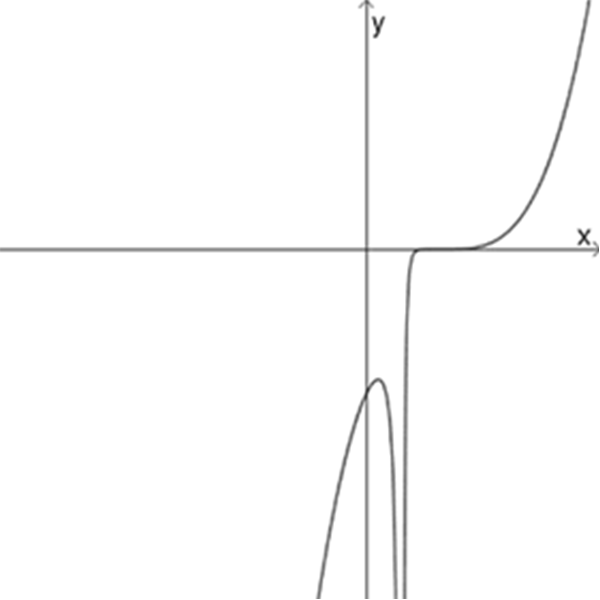
ח
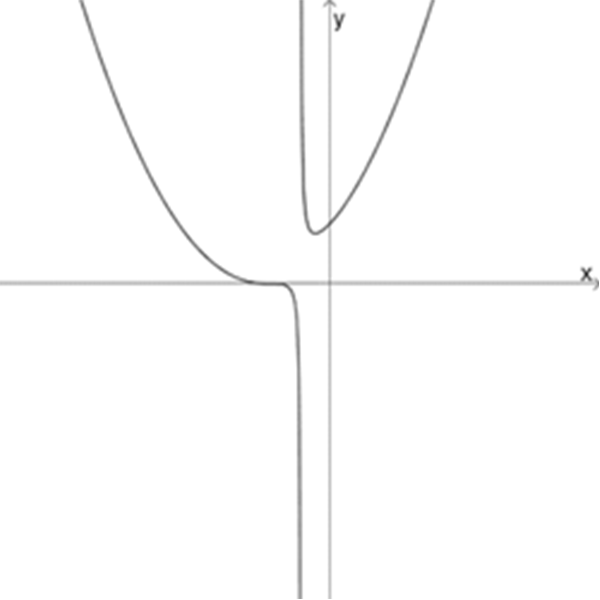
\(f_{10}(x)=\Large\frac{(x+2)^3}{x+1}\)
\(f_{11}(x)=\Large\frac{(x-3)^5}{(x-1)^2}\)
\(f_{12}(x)=\Large\frac{(x+2)^3}{(x+1)^2}\)
- במידת הצורך פתרו את הבעיות במדרגה 1.
מדרגה 1
לפניכם רשימה של פונקציות מהמשפחה: \(f{(x)}=\Large\frac{(x-a)^n}{(x-b)^m}\) , \(a \ne b\) , m , n טבעיים גדולים מ- 1.
מיינו את הפונקציות לפי התכונות הבאות:
- פונקציות שציר ה-x הוא אסימפטוטה אופקית שלהן.
- פונקציות שהישר: y=1 הוא אסימפטוטה אופקית שלהן.
- פונקציות שאין להן אסימפטוטה אופקית.
- פונקציות ללא אסימפטוטה אופקית, ששואפות ל-\(+\infty\) בשני "הקצוות" של ציר ה-x.
- פונקציות ללא אסמפטוטה אופקית, ששואפות ל-\(+\infty\) בקצה הימני של ציר ה-x ול-\(-\infty\) בקצה השמאלי שלו.
- פונקציות שהגבולות שלהן משני צידי האסימפטוטה האנכית שוני סימן.
- פונקציות שהגבולות שלהן משני צידי האסימפטוטה האנכית שווי סימן.
- פונקציות שהגרף שלהן משיק לציר ה-x.
- פונקציות שהגרף שלהן חותך את ציר ה-x ושיפוע המשיק בנקודת החיתוך אינו אפס.
- פונקציות שהגרף שלהן חותך את ציר ה-x בנקודת פיתול, בה הנגזרת הראשונה מתאפסת.
\(f_{1}(x)=\Large\frac{(x-1)^4}{(x+1)^4}\)
\(f_{2}(x)=\Large\frac{(x-2)^3}{(x-3)^2}\)
\(f_{3}(x)=\Large\frac{(x+1)^2}{(x+3)^3}\)
\(f_{4}(x)=\Large\frac{x^3}{(x-1)^4}\)
\(f_{5}(x)=\Large\frac{(x+1)^5}{(x+2)^3}\)
\(f_{6}(x)=\Large\frac{(x+1)^4}{(x+2)^2}\)
\(f_{7}(x)=\Large\frac{x-2}{(x+1)^4}\)
\(f_{8}(x)=\Large\frac{x-1}{x}\)
תוכלו להיעזר ביישומון.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
\(k(x)=\Large\frac{(x-1)^4}{(x-2)^2}\)
\(h(x)=\Large\frac{(x-1)^3}{(x-2)^2}\)
\(f(x)=\Large\frac{(x-1)^2}{(x-2)^2}\)
\(n(x)=\Large\frac{(x-1)^2}{(x-2)^4}\)
\(m(x)=\Large\frac{(x-1)^2}{(x-2)^3}\)
א
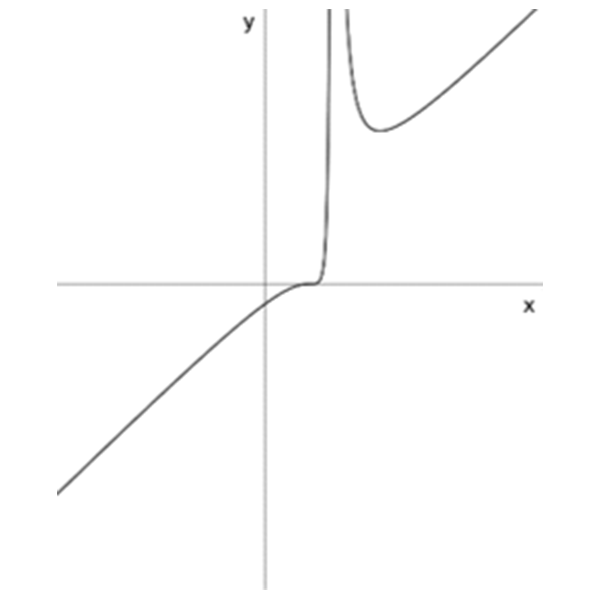
ב

ג
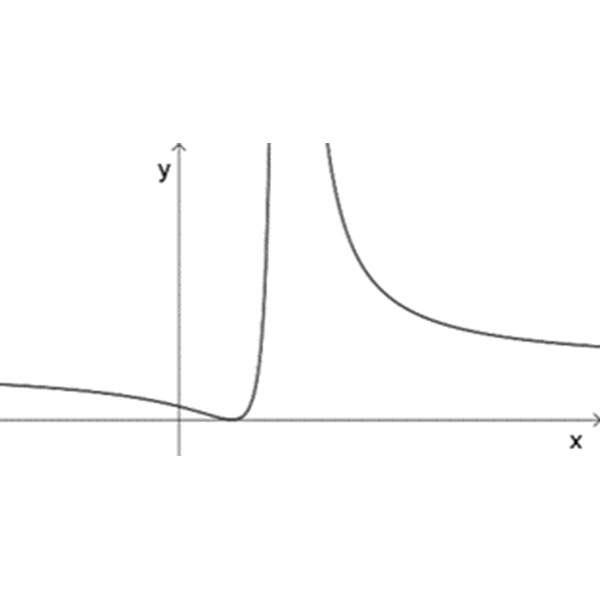
ד
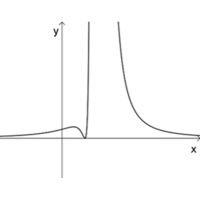
ה
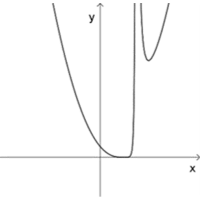
תוכלו להיעזר ביישומון.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.





















