משפט תלמי - למורה
חומר לימוד:
חזרה וביסוס של הידע בגיאומטריה ואפשרות של שילוב עם טריגונומטריה.
כיתה:
כיתה י' או י"א
מבנה המשימה:
בעיית מטרה ושלוש מדרגות, לכל סעיף מותאמים יישומונים.
ידע קודם:
הפעילות מתאימה לשימוש באחד משני שלבים בהוראה:
- בסיום לימודי הגיאומטריה, ללא שילוב טריגונומטריה:
- דמיון משולשים.
- זוויות היקפיות ומיתרים במעגל.
- תכונות מרובע חסום במעגל.
- שטחים.
- בשילוב טריגונומטריה, לשימוש ב:
- נוסחה למציאת שטח משולש בטריגונומטריה (לא הכרחי).
מטרות לימודיות:
- חזרה, ביסוס והעמקה של מכלול הידע בגיאומטריה.
- פתרון חלק מהבעיות בדרכים שונות.
משימת המטרה:
שני סעיפים: בסעיף א' הוכחת משפט תלמי ובסעיף ב' בעיה נוספת בה ניתן ליישם את משפט תלמי.
מדרגה 1:
טיפול בשאלה חלקית לזו המופיעה בבעיית המטרה. השאלה מתמקדת בזוג משולשים דומים, בשילוב יישומון.
מדרגה 2:
שאלה המתמקדת בטרפז שווה שוקיים.
מדרגה 3:
בדומה למדרגה 2 אך ההתמקדות בהיבט מצומצם יותר של השאלות.
שיטת הוראה:
בכיתה:
התלמידים יעבדו בזוגות או כיחידים. יעברו בין המדרגות השונות לפי בקשתם או לפי הנחיית המורה.
הערה:
המשימה: "קשר בין אלכסוני מרובע לצלעותיו" היא משימה מקדימה למשימה זו.
המשימה המקדימה מתמקדת בהוכחת משפט תלמי במקרים פרטיים (ללא שימוש במשפט): במלבן, טרפז שווה שוקיים ובדלתון בו זוויות הנגדיות ישרות.
יחד עם זאת ניתן להפעיל כל אחת מהמשימות הללו בנפרד.
שימוש ביישומונים:
לכל אחת מהמדרגות יש יישומון.
הערות נוספות למורה
- ניתן לבקש מהתלמידים לחפש באינטרנט מידע לגבי האיש תלמי ומקומו בהיסטוריה של המתמטיקה
- ניתן להמשיך ולהוכיח את משפט הקוסינוסים בעזרת משפט תלמי (כמובן, במקרה בו לא נעשה שימוש במשפט זה לפתרון המשימה)
- ניתן להרחיב את משפט תלמי
משימות מומלצות
- משימה מקדימה – קשר בין אלכסוני מרובע לצלעותיו
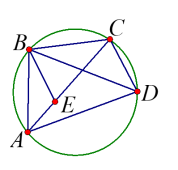
בניית עזר: העבירו קטע \(BE\) כך ש: \(\measuredangle CBD=\measuredangle ABE\)
- משולש \(ABC\) חסום במעגל.
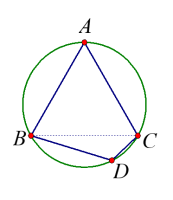
ונתון כי: \(AB=AC=BC\)
הנקודה \(D\) נמצאת על הקשת הקטנה \(BC\).
בטאו את שטח המרובע \(ABDC\) בעזרת \(AD\).
- במידת הצורך פתרו את הבעיות במדרגה 1.
פתרון לבעיית המטרה, סעיף 2
לפי משפט תלמי:
\(AD=BD+DC\)
באמצעות הורדת אנכים לאלכסון \(AD\) ושימוש במשפט פיתגורס במשולש 30, 60, 90, או מתוך שיקולים טריגונומטריים מקבלים:
\(S_{ABDC}=\Large\frac{\sqrt{3}\cdot{AD}^2}{4}\)
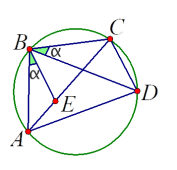
- מצאו משולשים דומים בסרטוט.
- הוכיחו כי: \(AD \cdot BC = DB \cdot EC\)
תוכלו להיעזר ביישומון.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
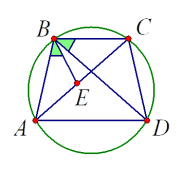
ונתון כי: \(\measuredangle CBD=\measuredangle ABE\).
- הוכיחו כי: \(\measuredangle BEC=\measuredangle DAB\).
- הוכיחו כי: \(AB \cdot DC + AD \cdot BC= DB \cdot AC\)
תוכלו להיעזר ביישומון.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.

הוכיחו כי: \(AB^2= AE \cdot BD\)
תוכלו להיעזר ביישומון.
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.





















