קשר בין אלכסוני מרובע לצלעותיו - למורה
חומר לימוד:
חזרה וביסוס של הידע בגיאומטריה ואפשרות של שילוב עם טריגונומטריה ומשפט הקוסינוסים.
כיתה:
כיתה י' (בסיום גיאומטריה) או כיתה י"א
מבנה המשימה:
בעיית מטרה אחת ושלוש מדרגות.
ידע קודם:
הפעילות מתאימה לשימוש באחד משני שלבים בהוראה:
- בסיום לימודי הגיאומטריה ללא שילוב הוכחות בעזרת טריגונומטריה כאשר מעוניינים לדון בתכונות מרובעים, משפט פיתגורס, שטח של מרובע שאלכסוניו מאונכים, ותכונות מרובע חסום במעגל.
- לתרגול יישומי טריגונומטריה במישור: משפט פיתגורס ו/או משפט הקוסינוסים.
מטרות לימודיות:
הפעילות מאפשרת:
- חזרה, ביסוס והעמקה של מכלול הידע בגיאומטריה.
- פתרון חלק מהבעיות בדרכים נוספות הנעזרות בכלים טריגונומטריים.
- פתרון שאלות בדרכים שונות וקישור בין שני התחומים.
משימת המטרה:
בבעיה ארבעה סעיפים הקשורים למלבן, טרפז שווה שוקיים ודלתון.
מדרגה 1:
שאלה אחת פרמטרית בטרפז שווה שוקיים, בה יש להביע את אלכסון הטרפז.
מדרגה 2:
שתי שאלות: אחת בטרפז שווה שוקיים פשוטה יותר ואחת בדלתון.
מדרגה 3:
שלוש שאלות: שתיים בטרפז שווה שוקיים המשלבות מספרים עם פרמטרים ואחת בדלתון.
שיטת הוראה:
בכיתה:
התלמידים יעבדו (רצוי בזוגות) בהתאם למדרגה בה הם בוחרים או בהתאם להכוונת המורה. בדיון הכיתתי תלמידים יציגו דרכים שונות לפתרון השאלות.
הערה:
המשימה "משפט תלמי" היא משימת המשך למשימה זו.
משימה זו מתמקדת בהוכחת המשפט: אם ניתן לחסום מרובע במעגל, אז מכפלת האורכים של אלכסוניו שווה לסכום המכפלות של אורכי הצלעות הנגדיות שלו ובשאלות נוספות בהן ניתן ליישם משפט זה.
משימות מומלצות:
- משימת המשך – משפט תלמי
בעיית מטרה
- הוכיחו כי במלבן מתקיימת התכונה: מכפלת האורכים של אלכסוני המלבן שווה לסכום המכפלות של אורכי הצלעות הנגדיות שלו.
- הוכיחו בדרכים שונות כי בטרפז שווה שוקיים מתקיימת התכונה: מכפלת האורכים של אלכסוני הטרפז שווה לסכום המכפלות של אורכי הצלעות הנגדיות שלו.
- הוכיחו כי בדלתון בו הזוויות הצדדיות ישרות מתקיימת התכונה: מכפלת האורכים של אלכסוני הדלתון שווה לסכום המכפלות של אורכי הצלעות הנגדיות שלו.
- אם למדתם על מעגל: איזו תכונה משותפת נוספת ישנה למלבן, לטרפז שווה שוקיים ולדלתון בו הזוויות הצדדיות ישרות?
- במידת הצורך, פתרו את הבעיות במדרגה 1.
פתרונות חלקיים
הצעות להוכחה שבטרפז שווה שוקיים הטענה מתקיימת:
צ"ל: \(AC\cdot{BD}=AD\cdot{BC}+DC\cdot{AB}\)
דרך א (ללא טריגונומטריה)
בניית עזר: \(AE\) אנך ל- \(DC\) ו- \(BF\) אנך ל- \(DC\).
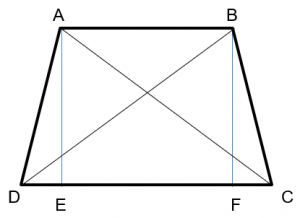
ניתן להוכיח כי:
\(DE=FC =0.5 \cdot{(DC-AB})\)
משפט פיתגורס ב- \(\triangle{ADE}\):
\(AE^2=AD^2-DE^2=AD^2-0.25(DC-AB)^2=\)
\(AD^2-0.25DC^2+0.5AB\cdot DC-0.25AB^2\)
משפט פיתגורס ב- \(\triangle{AEC}\):
\(EC=AB+FC=0.5\cdot(AB+DC)\)
\(AE^2=AC^2-EC^2=AC^2-0.25(AB+DC)^2=\)
\(AC^2-0.25AB^2-0.5AB⋅DC-0.25DC^2\)
לכן:
\(AC^2-0.25AB^2-0.5AB\cdot{DC}-0.25DC^2=AD^2-0.25DC^2+0.5AB\cdot{DC}-0.25AB^2\)
\(AC^2=AD^2+AB\cdot{DC}\)
בטרפז שווה שוקיים – השוקיים שוות. לכן: \(AD^2=AD\cdot{BC}\),
והאלכסונים בטרפז שווה שוקיים – שווים זה לזה. לכן: \(AC^2 = AC\cdot{BD}\)
נקבל: \(AC\cdot{BD} = AD\cdot{BC} +AB\cdot{DC}\)
דרך ב (בעזרת טריגונומטריה)
הצעה להוכחה שבטרפז שווה שוקיים הטענה מתקיימת:
צ"ל: \(AC\cdot{BD}=AD\cdot{BC}+DC\cdot{AB}\)
הוכחה:
בניית עזר: \(AE\) אנך ל- \(DC\)
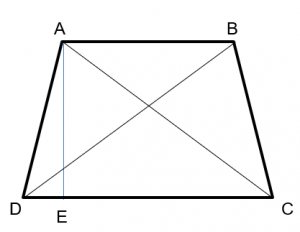
על פי משפט הקוסינוסים במשולש \(ADC\):
\({AC}^2={AD}^2+{DC}^2-2\cdot{AD}\cdot{DC}\cdot{cos\sphericalangle{ADC}}\)
\(DE =0.5\cdot{(DC-AB)}\)
במשולש ישר זווית \(ADE\):
\(cos{\sphericalangle{ADC}}=\Large\frac{0.5(DC-AB)}{AD}\)
לכן:
\(AC^2=AD^2+DC^2-2\cdot{AD}\cdot{DC}\cdot{\Large\frac{0.5(DC-AB)}{AD}}\)
\(AC^2=AD^2+DC^2-DC^2+DC\cdot{AB}\)
\(AC^2=AD^2+DC\cdot{AB}\)
בטרפז שווה שוקיים – השוקיים שוות: \(AD = BC\)
והאלכסונים שווים זה לזה: \(AC= BD\).
לכן:
\(AC\cdot{BD}=AD\cdot{BC}+DC\cdot{AB}\)
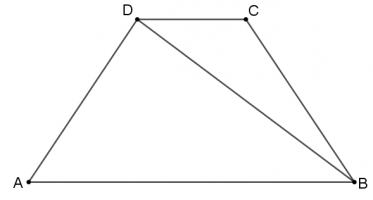
נתון כי: \(AD=k\) , \(DC=b\) , \(AB=a\)
הביעו את \(DB\) בעזרת \(k\) , \(b\) , \(a\).
מצאו לפחות שתי דרכים שונות.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
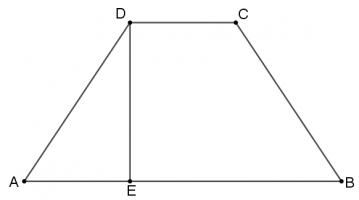
סעיף א
- הביעו את גובה הטרפז בעזרת \(k\) , \(b\) , \(a\).
- נסמן את זווית \(\measuredangle DAB\) ב- \(\alpha\), הביעו את \(cos \space \alpha\) בעזרת \(k\) , \(b\) , \(a\).
סעיף ב
הוכיחו כי שטח דלתון שווה למחצית מכפלת אלכסוניו.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
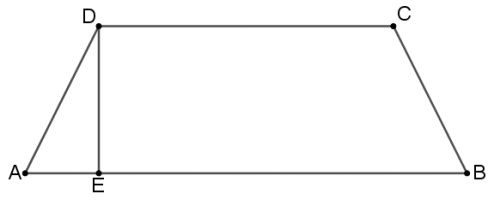
סעיף א
- הביעו את גובה הטרפז בעזרת \(k\).
- נסמן את זווית \(\measuredangle DAB\) ב- \(\alpha\), הביעו את \(cos \space \alpha\) בעזרת \(k\).
סעיף ב
\(ABCD\) טרפז שווה שוקיים.
נתון כי: \(AD=k \space cm\) , \(DC=8 \space cm\) , \(AB=12 \space cm\)
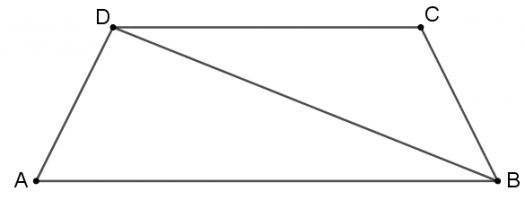
הביעו את \(DB\) בעזרת \(k\).
מצאו לפחות שתי דרכים שונות.
סעיף ג
\(ABCD\) דלתון בו זוויות הצד ישרות, בטאו את שטח הדלתון בשני אופנים שונים.
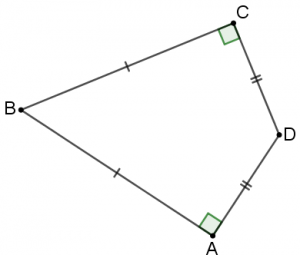
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.




