פונקציות עם שורשים ריבועיים – מה ההבדל בינינו? חלק ב' - למורה
חומר לימוד:
חקירת פונקציות עם שורשים ריבועיים
כיתה:
כיתה י"א
מבנה המשימה:
משימת מטרה ושתי מדרגות. מומלץ להיעזר במחולל גרפים רק לצורך בדיקה.
ידע קודם:
- חוקי חזקות/שורשים (ללא התייחסות לשורש ריבועי כמעריך שבור). הכרות עם פונקציית השורש הריבועי, מיומנויות חקירת פונקציות באמצעות נגזרות.
- הכרות עם פונקציית השורש הריבועי
- מיומנויות חקירת פונקציות באמצעות נגזרות.
מטרות לימודיות:
- בחינת ההבדלים בין \(\sqrt{x^{2n}}\) ל- \(x^n\) כאשר \(n\) זוגי וכאשר \(n\) אי זוגי.
- בחינת ההבדלים בין שורש של מכפלה לבין מכפלה של שורשים, או מצב דומה, כאשר מתחת לשורש מופיעה מכפלה של פולינום ריבועי ב- \(x^{2n}\) , \(n\) טבעי.
- בחינת ההבדלים בין שורש של מנה לבין מנה של שורשים או מצב דומה, כאשר מתחת לשורש מופיעה מנה של פולינום ריבועי ב- \(x^{2n}\) , \(n\) טבעי.
משימת המטרה:
במשימת המטרה ארבעה זוגות של פונקציות עם פרמטר יחיד. על התלמידים לאבחן את הבדלים בכל זוג ולסרטט גרפים מתאימים.
מדרגה 1:
ארבעה זוגות של פונקציות, ללא פרמטר, ושישה גרפים. יש להתאים בין פונקציה לגרף.
מדרגה 2:
ארבעה זוגות של פונקציות ללא פרמטרים, וליד כל זוג גרף המתאים לפחות לאחת הפונקציות.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות. המורה יחלק את בעיית המטרה לכולם. מי שמתקשה, יבחר לעצמו את המדרגה המתאימה.
שימוש ביישומונים:
מומלץ להשתמש במחולל גרפים (כמו: geogebra או desmos) רק לצורך בדיקה. (לבעיות לא קיימים יישומונים).
שיעורי בית:
סיום המשימה.
משימות מומלצות:
בעיית מטרה
נתונים ארבעה זוגות של פונקציות. נתון: \(a>0\).
בכל אחד מהזוגות:
- בחנו את תחום ההגדרה של הפונקציות.
- אפיינו את ההשפעה של השורש הריבועי על תחום ההגדרה ועל המראה של הגרף בקצוות התחום.
- סרטטו סקיצה אפשרית של כל אחת מהפונקציות.
- השתמשו במחולל גרפים (כמו: geogebra או desmos) לצורך בדיקה. (לבעיה לא קיים יישומון).
- \(f_{1}(x)=\sqrt{x^2(a-x^2)}\) לעומת: \(f_{2}(x)=x\sqrt{a-x^2}\)
\(\space\) - \(f_{3}(x)=\sqrt{x^4(a-x^2)}\) לעומת: \(f_{4}(x)=x^2\sqrt{a-x^2}\)
\(\space\) - \(f_{5}(x)=\sqrt{\Large\frac{a-x^2}{x^2}}\) לעומת: \(f_{6}(x)=\Large\frac{\sqrt{a-x^2}}{x}\)
\(\space\) - \(f_{7}(x)=\sqrt{\Large\frac{a-x^2}{x^4}}\) לעומת: \(f_{8}(x)=\Large\frac{\sqrt{a-x^2}}{x^2}\)
- במידת הצורך פתרו את הבעיות במדרגה 1.
א
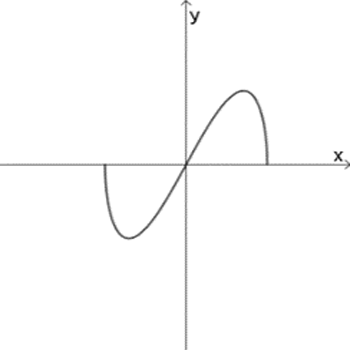
ג
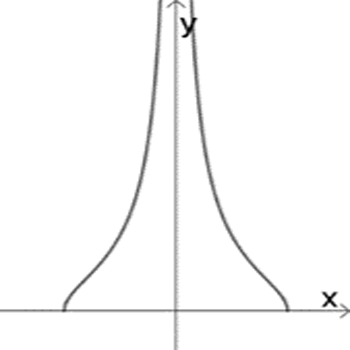
ה
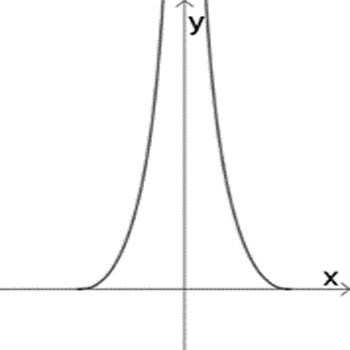
ב
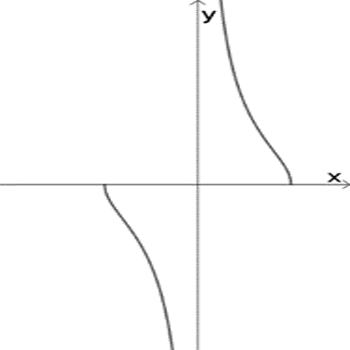
ד
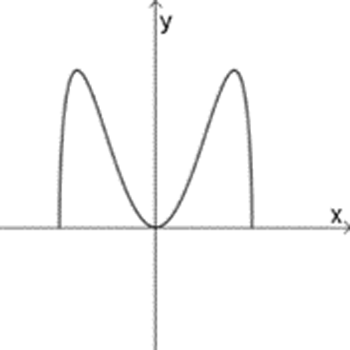
ו
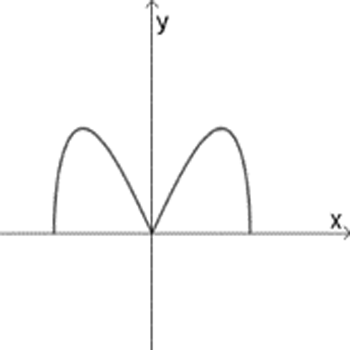
\(f_{1}(x)=\sqrt{x^2(4-x^2)}\)
\(f_{2}(x)=x\sqrt{4-x^2}\)
\(f_{3}(x)=x^2\sqrt{4-x^2}\)
\(f_{4}(x)=\sqrt{x^4(4-x^2)}\)
\(f_{5}(x)=\Large\frac{\sqrt{4-x^2}}{x}\)
\(f_{6}(x)=\sqrt{\Large\frac{4-x^2}{x^2}}\)
\(f_{7}(x)=\Large\frac{\sqrt{4-x^2}}{x^2}\)
\(f_{8}(x)=\sqrt{\Large\frac{4-x^2}{x^4}}\)
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
א
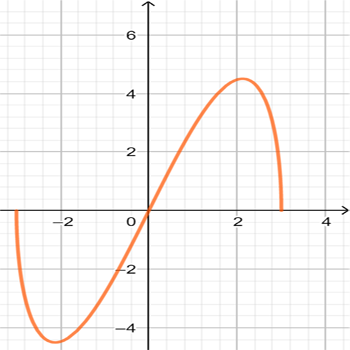
\(f_{2}(x)=\sqrt{x^2(9-x^2)}\)
\(f_{1}(x)=x\sqrt{9-x^2}\)
ב
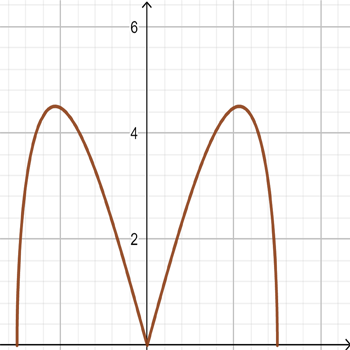
\(f_{4}(x)=\sqrt{x^2(9-x^2)}\)
\(f_{3}(x)=|x|\sqrt{9-x^2}\)
ג
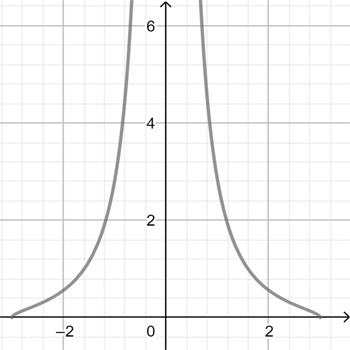
\(f_{6}(x)=\sqrt{\Large\frac{9-x^2}{x^4}}\)
\(f_{5}(x)=\Large\frac{\sqrt{9-x^2}}{x^2}\)
ד
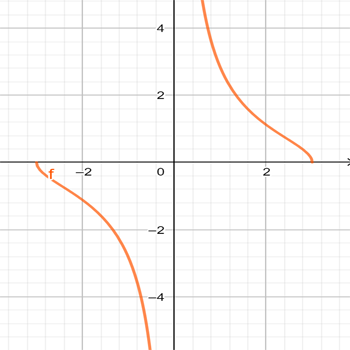
\(f_{8}(x)=\sqrt{\Large\frac{9-x^2}{x^2}}\)
\(f_{7}(x)=\Large\frac{\sqrt{9-x^2}}{x}\)
התאימו לכל גרף פונקציה. אם נחוץ, הוסיפו בעצמכם גרף לפונקציה השנייה.
נסו להציע סקיצות ללא חקירה וללא שימוש במחולל גרפים.
- בחנו את תחום ההגדרה של הפונקציות השונות.
- אפיינו את ההשפעה של השורש הריבועי על תחום ההגדרה ועל המראה של הגרף בקצוות התחום.
- השתמשו במחולל גרפים (כמו: geogebra או desmos) לצורך בדיקה. (לבעיה לא קיים יישומון).
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.





















