ישר ושתי נקודות – כמה פתרונות? - למורה
חומר לימוד:
מרחק נקודה מישר (גיאומטריה אנליטית).
המשימה מתאימה לשימוש באחד משני שלבים בהוראה:
- במהלך ההוראה של שימוש בנוסחת המרחק בין נקודה לישר. שילוב המשימה בהוראת נושא זה יאפשר הדגשה שבנוסחה המפורשת של ישר לא נכללים הישרים המאונכים לציר ה-\(x\), בנוסחת המרחק לפי משוואה כללית של ישר, נכללת כל משפחת הישרים.
- לאחר שפגשו גם את משוואת המעגל. שילוב המשימה כאן יהווה תרגול של כל הכלים האנליטיים בנושא ישר ומעגל ויאיר אפשרויות של פתרון בדרכים שונות. יהיה שימוש בחיתוך בין מעגלים, יכול להיות שימוש בהשקה של ישר למעגל כאשר הדיסקרימיננטה שווה אפס, וכמובן שימוש מושכל בנוסחת המרחק של נקודה מישר.
כיתה:
כיתה י"ב
מבנה המשימה:
בעיית מטרה ושתי בעיות מדרגה. לבעיית המטרה ולמדרגה 1 מצורף יישומון.
ידע קודם:
- נוסחת המרחק של נקודה מישר.
- בניות בעזרת סרגל ומחוגה.
- תכונות גיאומטריות ומשפטים בנושאים הבאים: שני משיקים למעגל מנקודה שמחוץ לו, רדיוס מאונך למשיק בנקודת ההשקה, תכונת חוצה זווית כמקום גיאומטרי של נקודות שנמצאות במרחקים שווים משוקי הזווית.
מטרות לימודיות:
- הדגשת חשיבות הבחינה של המצב הגיאומטרי בפתרון שאלות בגיאומטריה אנליטית
- הדגשה כי משוואה כללית של ישר כוללת את כל הישרים לעומת משוואה מפורשת שלא נכללים בה ישרים מאונכים לציר ה-\(x\)
- פתרון בדרכים שונות
- שילוב בניות באמצעות סרגל ומחוגה
משימת המטרה:
בעיה מורכבת בה יש למצוא משואת ישרים העוברים דרך נקודה כללית ומרחקם מנקודה נתונה קבוע.
מדרגה 1:
בעיה פחות מורכבת. נתונות משוואות ישרים והנקודות קבועות.
מדרגה 2:
בעיה פשוטה יותר.
אם עונים על הבעיות המופיעות במדרגות, נוגעים בכל הסוגיות המובילות לפתרון בעיית המטרה.
שיטת הוראה:
בכיתה:
עבודה עצמאית או בזוגות. התלמידים עוברים בין בעיית המטרה והמדרגות לפי בחירתם או בהנחית המורה.
הקו המשותף אליו חשוב שיגיעו כולם:
פתרון המשימה באמצעות נוסחת מרחק נקודה מישר והשוואה בין שימוש בנוסחה עבור הצגה של ישר במשוואה כללית לעומת הצגתו במשוואה מפורשת.
שימוש ביישומונים:
קיים יישומון לבעיית המטרה ולמדרגה 1.
שיעורי בית:
תלמידים שלא סיימו את המשימה בכיתה יסיימו כשעורי בית.
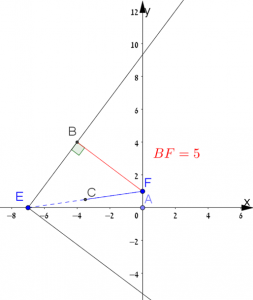
מקרה א – עובר דרך הנקודה \(E(-7,0)\) ומרחקו מהנקודה \(F(0,1)\) הוא: 5 יחידות.
(כמה פתרונות יש?)
מקרה ב – עובר דרך \((5,e)\) ומרחקו מהנקודה \((0,1)\) הוא: 5 יחידות.
- כמה ישרים יהיו עבור e≠1?
- כמה ישרים יהיו עבור e=1?
עימדו על ההבדלים בין מקרה א' למקרה ב'.
- במידת הצורך פתרו את הבעיות במדרגה 1.
פתרונות (חלקיים) לבעיית המטרה
להלן סרטוטים שמדגימים את המצבים בכל אחד מסעיפי המשימה:
מקרה א
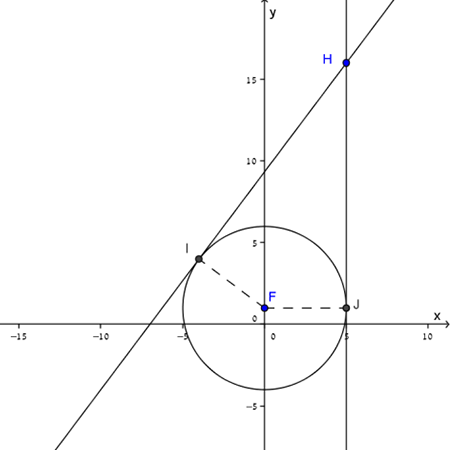
מקרה ב
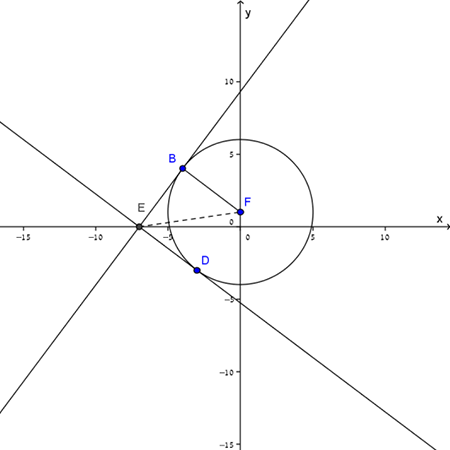
מקרה א (סרטוט ימני)
משוואות הישרים שעוברים בנקודה \((-7 ,0)\) ומרחקם מהנקודה \((0 ,1)\) הוא \(5\) הן:
\(-3x-4y=21\) , \(-4x+3y=28\)
שלוש דרכים לפתרון:
- טריגונומטרית: המשולשים \(\triangle EBF\) ו- \(\triangle EDF\) הם ישרי זווית.
ניתן לחשב את זוויותיהם ולמצוא את הערכים המדוייקים של השיפועים של הישרים המבוקשים. - חיתוך בין מעגלים: הנקודות \(B\) ו-\(F\) הן נקודות חיתוך של מעגל ברדיוס \(5\) סביב הנקודה \((0 ,1)\) ומעגל שקצות קוטרו בנקודות: \((0 ,1)\) ו- \((-7 ,0)\).
- מרחק נקודה מישר: רושמים משוואה של ישר (כללית או מפורשת) שעובר בנקודה \((-7 ,0)\). במשוואה יש נעלמים.
דורשים שמרחק הישר מהנקודה \((0 ,1)\) יהיה \(5\).
מקבלים שני פתרונות, גם כאשר המשוואה של הישר נרשמה בצורתה המפורשת.
מקרה ב (סרטוט שמאלי)
משוואות הישרים שעוברים דרך \((5 ,16)\) ומרחקם מהנקודה \((0 ,1)\) הוא: \(5\) יחידות הן:
\(x=5\) , \(-4x+3y=28\)
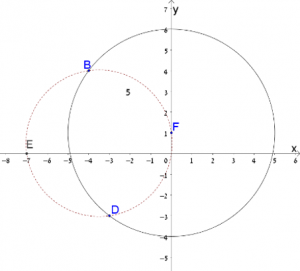
- מצאו את נקודות החיתוך של שני המעגלים.
- הישר: \(-4x+3y=28\) עובר דרך הנקודה \((-7,0)\) ודרך אחת מנקודות החיתוך של שני המעגלים, הנקודה B (ראו סרטוט). מצאו את מרחקו מהנקודה \((0,1)\).
- מצאו, אם אפשר, ישר נוסף שעובר דרך הנקודה \((-7,0)\) ומרחקו מהנקודה \((0,1)\) הוא 5 יחידות.
סעיף ב
נתונים שני מעגלים:
מעגל שמרכזו בנקודה \((0,1)\) ורדיוסו 5 יחידות, ומעגל שקצות קוטר שלו בנקודות \((5,16)\) ו-\((0,1)\) .
- מצאו את נקודות החיתוך של שני המעגלים.
- הישר: \(-4x+3y=28\) עובר דרך הנקודה \((5,16)\). מצאו את מרחקו מהנקודה \((0,1)\).
- מצאו, אם אפשר, ישר נוסף שעובר דרך הנקודה \((5,16)\) ומרחקו מהנקודה \((0,1)\) הוא 5 יחידות.
תוכלו להיעזר ביישומון המצורף, הזיזו את הנקודה \(E\) למקום המתאים.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- הזיזו את הנקודה \(E\) למקום המתאים.
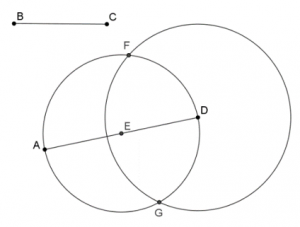
- מה תוכלו לומר על הקטעים \(AG\), \(AF\) ו- \(AD\)?
- מהו המרחק של הישר \(AF\) מהנקודה \(D\)?
- מצאו, אם אפשר, ישר נוסף שמרחקו מהנקודה \(D\) שווה למרחק שמצאתם בסעיף 2.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.





















