פונקציה מעריכית מורכבת \(e^{f{(x)}}\) - חלק ב' - למורה
חומר לימוד:
סרטוט הגרפים של הפונקציות \(e^{f{(x)}}\) , \(n\) טבעי, כאשר נתון גרף הפונקציה \(f{(x)}\).
משימה לסיכום הנושא, מתאימה להפעלה לאחר המשימה "פונקציה מעריכית מורכבת חלק א' ".
כיתה:
כיתה י"ב
מבנה המשימה:
בעיית מטרה, שלוש מדרגות ובעיית אתגר. לכולן מצורפים יישומונים.
ידע קודם:
- הכרת התכונות של הפונקציה \(e^x\).
- הכרת הקשרים בין גרף של פונקציה \(f{(x)}\) לבין גרפים של הפונקציות \(f^n{(x)}\) עבור \(n\) זוגי ו-\(n\) אי זוגי.
- תכונות של פונקציה כמו: נקודות חיתוך עם הצירים, נקודות קיצון וסוגן, תחומי עליה וירידה, תחומי חיוביות ושליליות, נקודות פיתול, אסימפטוטות מאונכות לצירים, התנהגות פונקציה בקצה תחום הגדרה.
מטרות לימודיות:
- אפיון קשרים בין תכונות הגרף של פונקציה \(f{(x)}\) לבין גרף הפונקציה \(e^{f{(x)}}\).
- אפיון קשרים בין תכונות הגרף של פונקציה \(f{(x)}\) לבין גרף הפונקציה \(e^{f^2{(x)}}\).
- אפיון קשרים בין תכונות הגרף של פונקציה \(f{(x)}\) לבין גרף הפונקציה \(e^{f^3{(x)}}\).
- הכללה לגבי קשרים בין תכונות גרף של פונקציה \(f{(x)}\) לבין גרפים של הפונקציות \(e^{f^n{(x)}}\) עבור \(n\) טבעי זוגי ו-\(n\) טבעי אי זוגי.
בבדיקת הקשרים אין הכרח להיעזר בנגזרת. ניתן, לאחר סרטוט הגרף המבוקש, לבדוק את הביטוי הכללי של הנגזרת ולוודא התאמה של תכונותיו למאפייני הגרף שהתקבל.
משימת המטרה:
בבעיית המטרה לפונקציה יש שתי נקודות קיצון, נקודת חיתוך אחת עם ציר ה-\(x\) ואסימפטוטות אופקית ואנכית. למסיימים את בעיית המטרה ישנן שאלות אתגר.
המדרגות בנויות משאלות הממקדות את תשומת הלב בנקודות מסוימות בבעיית המטרה.
מדרגה 1:
במדרגה 1 לפונקציה יש אסימפטוטות אנכית ואופקית, נקודת חיתוך אחת עם ציר \(x\) ואין לה נקודות קיצון.
מדרגה 2:
במדרגה 2 לפונקציה יש שתי נקודות קיצון, שלוש נקודות חיתוך עם ציר \(x\) ואין לה אסימפטוטות.
מדרגה 3:
במדרגה 3 הפונקציות הן פרבולות אחת בעלת מינימום והשנייה בעלת מקסימום ועל התלמיד לבחור את הגרפים המתאימים להרכבה של הפונקציה \(e^x\) עליהן ועל חזקות שלהן מתוך גרפים נתונים.
המדרגות בנויות משאלות הממקדות את תשומת הלב במאפיינים שמופיעים בבעיית המטרה.
שיטת הוראה:
בכיתה:
התלמידים יעבדו בזוגות, הם ייחשפו תחילה לבעיית המטרה. תוך כדי העבודה בכיתה המורה ינחה את התלמידים להשתמש בבעיות המדרגה, בהתאם להתקדמותם, בהתאם לקשיים בהם ייתקלו במהלך עבודתם, ו/או בהתאם לבקשת התלמידים.
תלמידים שפתרו את בעיית המטרה ללא עזרת המדרגות יכולים להמשיך ולפתור את תרגילי האתגר.
שימוש ביישומונים:
יש
שיעורי בית:
כשיעורי בית ניתן לתת את שאלות האתגר ו/או פתרון כל השאלות שבבעיות המדרגה.
משימות מומלצות:
\(t(x)\)
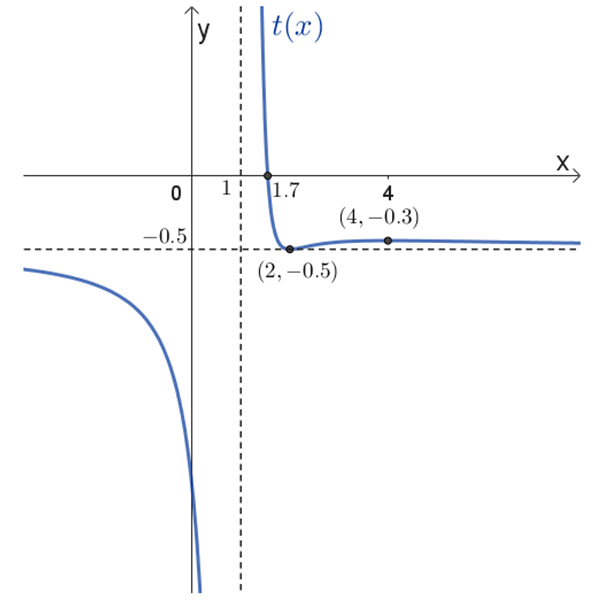
תחום ההגדרה: \(x≠1\)
נקודות החיתוך של הפונקציה עם הצירים הן: \((1.7 ,0)\) , \((0 ,-6.5)\)
נקודות הקיצון: \((4 ,-0.3)\) , \((2 ,-0.5)\)
אסימפטוטות: \(x=1\) , \(y=-0.5\)
- סרטטו את הגרפים של הפונקציות: \(e^{t{(x)}}\) , \(e^{t^2{(x)}}\) , \(e^{t^3{(x)}}\) במערכות צירים נפרדות.
- תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- עיברו לפתרון בעיית האתגר.
- במידת הצורך, פתרו את הבעיות במדרגה 1.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון
שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה. - ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפונקציה המעריכית \(e^{t^n{(x)}}\) הבאה, יש ללחוץ על החץ בתיבה הכחולה שיופיע בסיום סרטוט תקין.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ 
בתפריט העליון. - כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול
שבפינה הימנית העליונה.
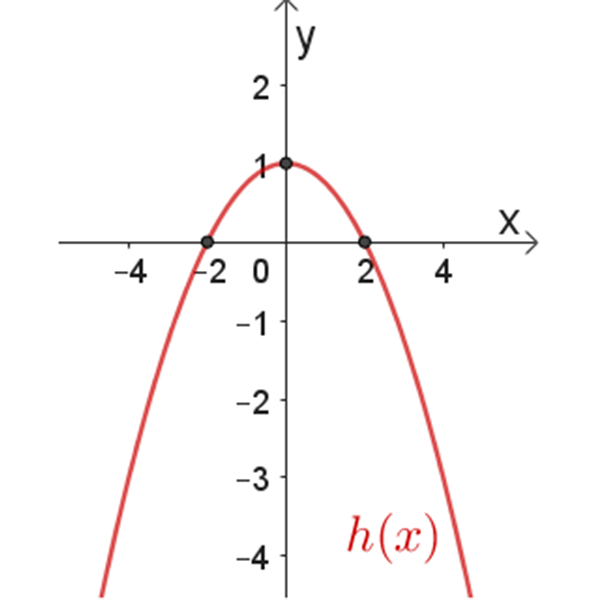
\(h(x)\)
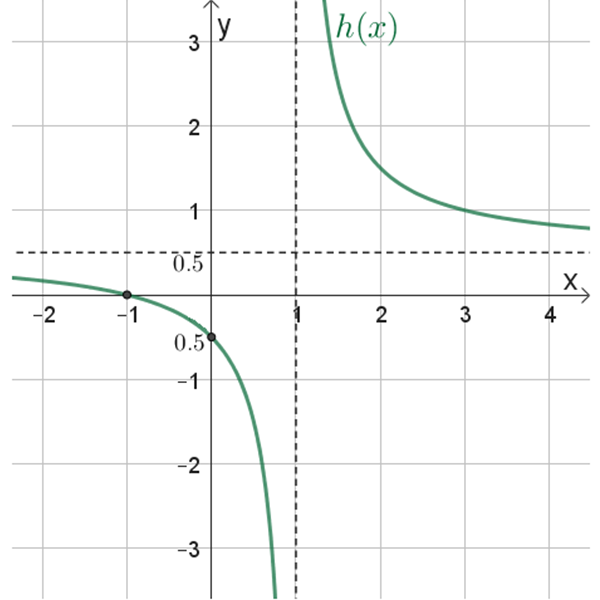
תחום ההגדרה: \(x≠1\)
נקודות חיתוך עם הצירים: \((0 ,-0.5)\) , \((-1 ,0)\)
אסימפטוטות: \(x=1\) , \(y=0.5\)
- סרטטו את הגרפים של הפונקציות: \(e^{h{(x)}}\) , \(e^{h^2{(x)}}\) , \(e^{h^3{(x)}}\) במערכות צירים נפרדות.
- תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 1, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 2.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפונקציה המעריכית \(e^{h^n{(x)}}\) הבאה, יש ללחוץ על החץ בתיבה הכחולה שיופיע בסיום סרטוט תקין.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
\(f(x)\)
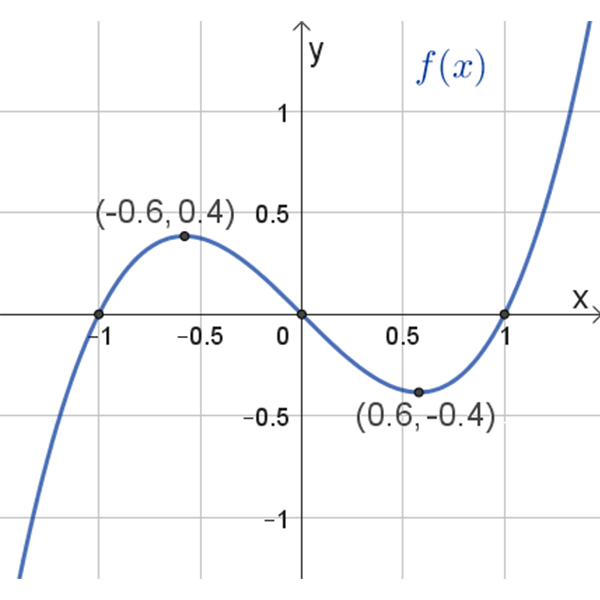
נקודות חיתוך עם הצירים: \((1,0)\) , \((0,0)\) , \((-1,0)\)
נקודות קיצון: \((0.6,-0.4)\) , \((-0.6,0.4)\)
במערכות צירים נפרדות, סרטטו את הגרפים של הפונקציות הבאות:
- \(f^3{(x)}\) , \(f^2{(x)}\)
- \(e^{f^3{(x)}}\) , \(e^{f^2{(x)}}\) , \(e^{f{(x)}}\)
תוכלו לסרטט ולבדוק תשובותיכם בעזרת היישומון המצורף.
- אחרי שפתרתם את הבעיות במדרגה 2, פתרו את בעיית המטרה.
- או, במידת הצורך, פתרו את הבעיות במדרגה 3.
- יש לבחור את הפונקציה המתאימה ביישומון.
- מתוך מחסן הנקודות יש לגרור ולמקם לפחות שבע נקודות מלאות במקומות המתאימים להן ואת הנקודות הריקות (אם יש צורך, סימון נקודות אי רציפות סליקה).
- יש לסמן אסימפטוטות (במידה וישנן) על ידי גרירת הנקודה האדומה שעל הקווים האנכיים/אופקיים (במחסן הנקודות), אל המיקום המתאים.
- יש להיעזר בעיפרון שבתפריט העליון, ולסרטט את גרף הפונקציה החדשה.
- ניתן לבצע בדיקה רק לאחר מיקום של לפחות שבע נקודות מלאות ובמידת הצורך גם מיקום נקודות ריקות ואסימפטוטות.
- כדי לעבור לפונקציה המעריכית \(e^{f^n{(x)}}\) הבאה, יש ללחוץ על החץ בתיבה הכחולה שיופיע בסיום סרטוט תקין.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ בתפריט העליון.
- כדי ל"נקות" את היישומון ולהתחיל מחדש יש ללחוץ על הכפתור אתחול או להיעזר בחיצי האתחול שבפינה הימנית העליונה.
מדרגה 3
נתונים הגרפים של \(f(x)\) ושל \(h(x)\).
- לכל גרף, מבין הגרפים 1-6 הנתונים בהמשך, קבעו האם הוא מתאים לאחת מהפונקציות:
\(e^{f^3{(x)}}\) , \(e^{f^2{(x)}}\) , \(e^{f{(x)}}\)
\(e^{h^3{(x)}}\) , \(e^{h^2{(x)}}\) , \(e^{h{(x)}}\)
ואם הוא מתאים, קבעו לאיזו פונקציה הוא מתאים.
נמקו תשובתכם. - האם ישנם גרפים שיכולים להתאים ליותר מפונקציה אחת? נמקו תשובתכם.
גרפים של פונקציות נתונות:
\(f(x)\)
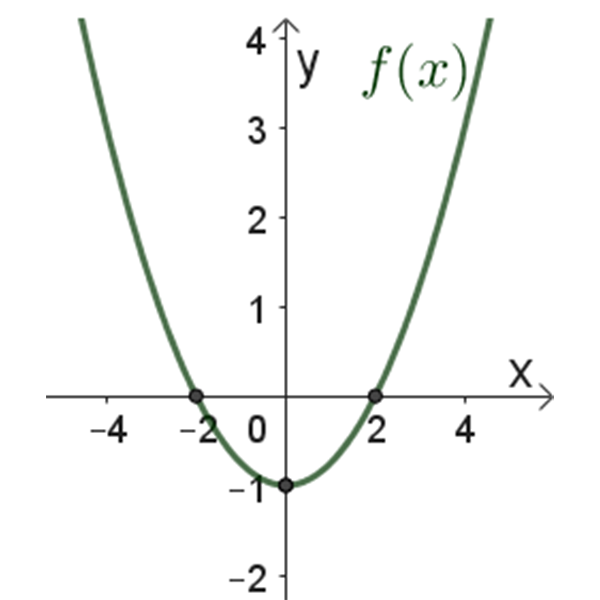
\(h(x)\)
גרפים של פונקציות מעריכיות:
1
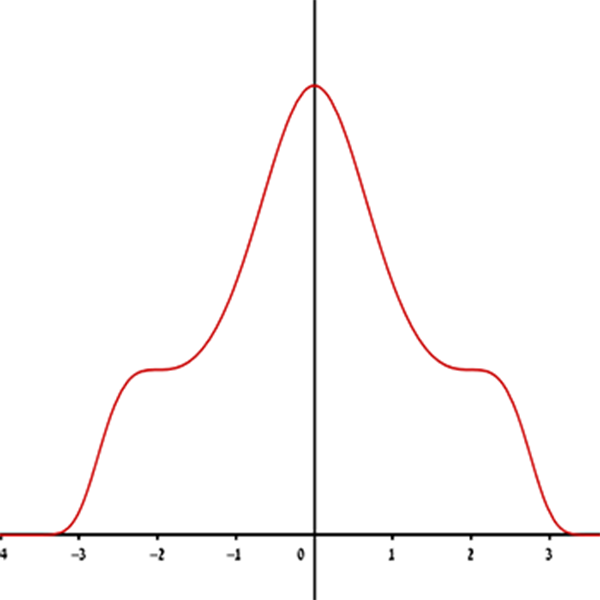
2
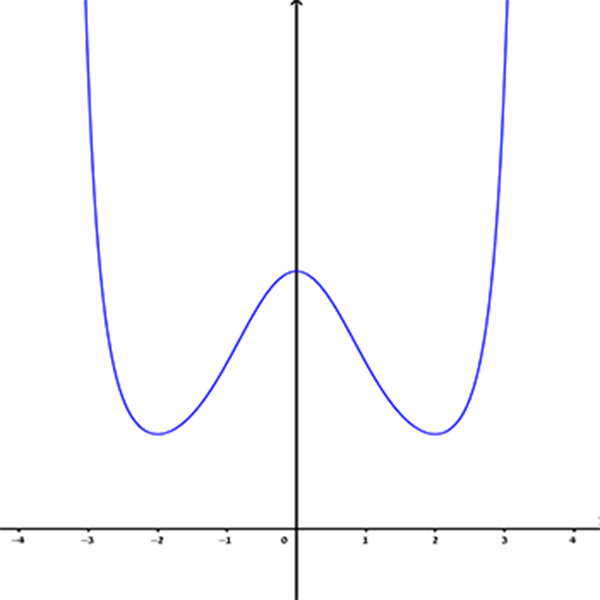
3
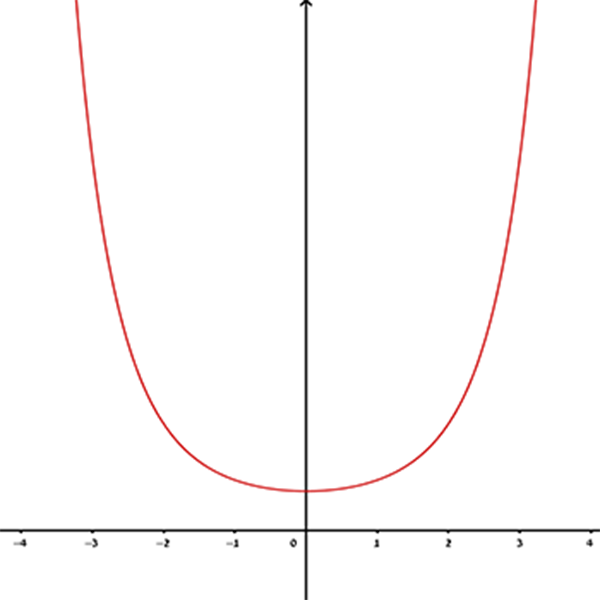
4
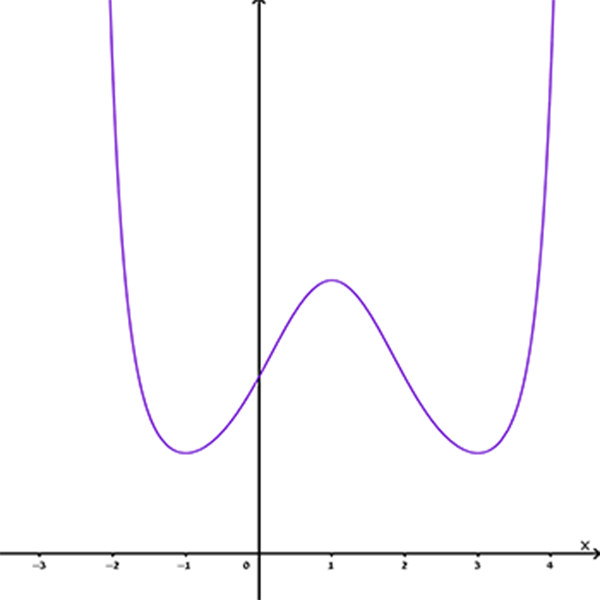
5
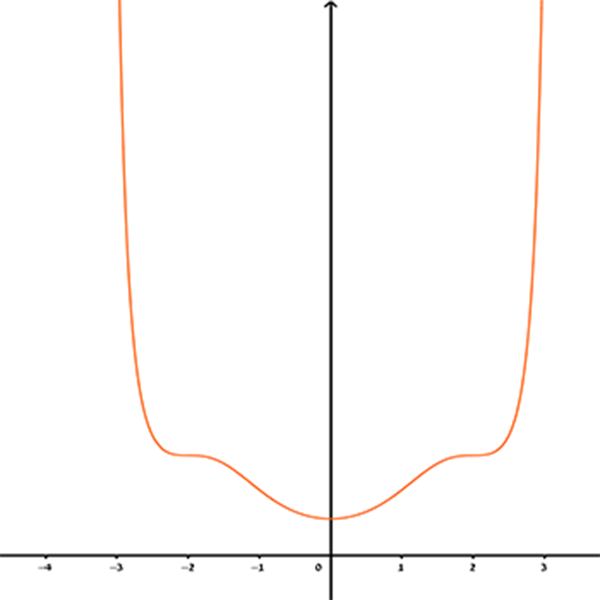
6
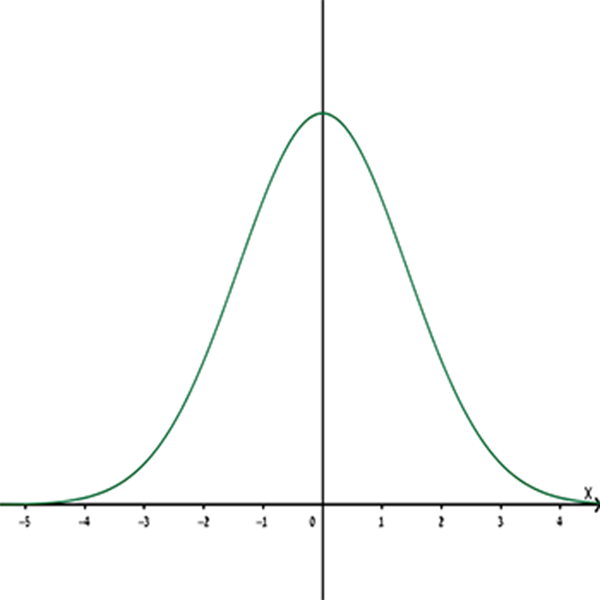
- אחרי שפתרתם את הבעיות במדרגה 3, פתרו את בעיית המטרה.
- ניתן להזיז את הפרבולה הזזה אופקית ואנכית בעזרת גרירת הנקודה הכתומה.
- ניתן למתוח את הפרבולה ואף להפוך אותה בעזרת גרירת הנקודה הכחולה.
בעיית אתגר
סעיף א
נתונה משפחת הפונקציות: \(g_n{(x)}=e^{f^n{(x)}}\) , \(n\) טבעי.
מצאו ביטוי של פונקציה \(f(x)\) כך שלכל פונקציה במשפחה זו לא תהיינה נקודות קיצון.
נמקו תשובתכם.
בדקו תשובתכם בעזרת היישומון המצורף.
סעיף ב
1. מצאו ביטוי/ביטויים לפונקציה \(f(x)\) כך שהגרפים של \(e^{f^3{(x)}}\) , \(e^{f^2{(x)}}\) , \(e^{f{(x)}}\) יתאימו לגרפים שבסרטוט הבא.
נמקו תשובתכם.
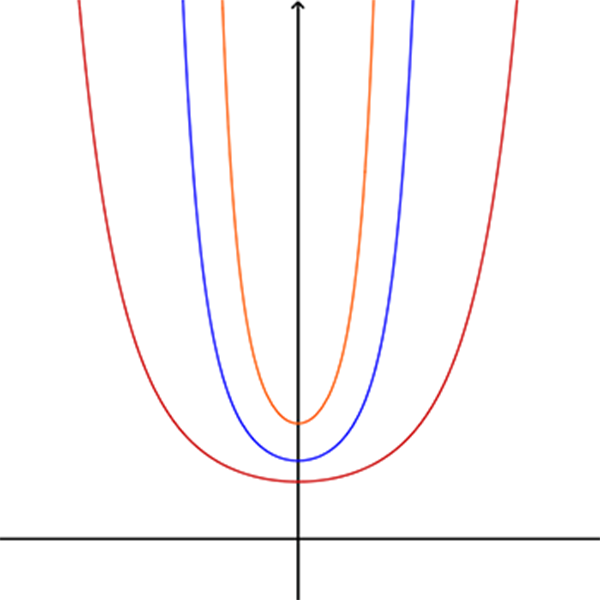
2. מצאו ביטוי/ביטויים לפונקציה \(h(x)\) כך שהגרפים של \(e^{h^3{(x)}}\) , \(e^{h^2{(x)}}\) , \(e^{h{(x)}}\) יתאימו לגרפים שבסרטוט הבא.
נמקו תשובתכם.
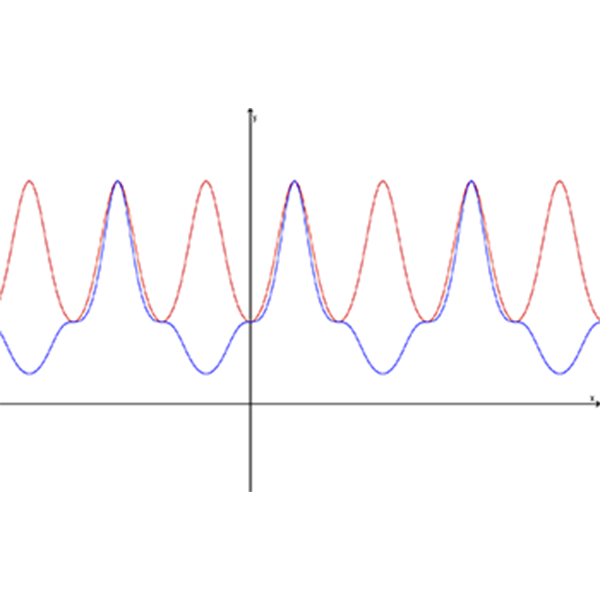
בדקו תשובתכם בעזרת היישומון המצורף.
- ניתן לכתוב ביטוי לפונקציה כלשהי ויופיע הגרף המתאים